
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Перевірка гіпотези про значущість коефіцієнтаСодержание книги
Поиск на нашем сайте
Рангової кореляції Спирмена
Для обґрунтованого судження про наявність зв'язку між розглянутими ознаками варто перевірити, чи значущій коефіцієнт рангової кореляції Спирмена при певному (досить малому) рівні значущості Нехай генеральна сукупність складається з об'єктів, що мають дві якісні ознаки Знайдемо критичну точку
де
Точка Якщо Якщо Приклад 1. По вибірці об'єму Розв’язання. За рівнем значимості
Знайдемо тепер критичну точку по формулі (2.4.2.1):
Тому що
Питання й задачі для самоперевірки
1. Чим відрізняється нелінійна регресія від лінійної? 2. Для чого вводиться кореляційне відношення? 3. У якому випадку можна затверджувати, що ознака 4. Чи можна затверджувати, що якщо кореляційне відношення дорівнює одиниці, то ознаки 5. Чим відрізняється множинна кореляція від парної? 6. Для чого вводяться коефіцієнти кореляції 7. У чому суть рангової кореляції? 8. Для чого здійснюється перевірка гіпотези про значущість коефіцієнта рангової кореляції?
Приклад 1. рівняння регресії
Таблиця 30
Відповідь. Приклад 2. Два товарознавці розташували дев'ять мотків пряжі в порядку убування товщини нитки. У підсумку були отримані дві послідовності рангів:
Знайти коефіцієнт рангової кореляції Спирмена між рангами
Відповідь.
Розділ 3. Однофакторний дисперсійний аналіз Постановка задачі На практиці часто доводиться вирішувати питання про те, якою мірою впливає той чи інший фактор або комбінація факторів на розглянуту результативну ознаку. Науково обґрунтовану відповідь на це питання дає дисперсійний аналіз. Залежно від кількості факторів, вплив яких на результативну ознаку досліджується, дисперсійний аналіз підрозділяється на однофакторний і багатофакторний. У загальному виді задачу однофакторного дисперсійного аналізу можна сформулювати в такий спосіб. Є одиничний фактор Допустимо, що на кожному рівні зроблений ряд спостережень. Потрібно визначити вплив фактору Важливість подібних оцінок випливає хоча б із двох наступних прикладів. Земна куля, крім добового обертання навколо своєї осі й річного обертання навколо Сонця, зазнає ще деякі слабкі коливання і переміщення. Ці переміщення вдається виявити, спостерігаючи за зірками. Однак переміщення так малі, що можуть бути прийняті просто за помилки спостережень, пов'язані з неточною роботою астрономічних інструментів (останнє, до речі й з'явилося причиною того, що переміщення, про які мова йде, були виявлені лише порівняно недавно). Перш ніж проводити детальне вивчення переміщень, виявити їх причини і т.д., необхідно перевірити в цілому, чи дійсно ці переміщення істотні на фоні випадкових погрішностей приладів. Другий приклад візьмемо із проблеми контролю за виробництвом. Від заводу звичайно потрібен випуск однорідної по своїх якостях продукції. Процес виробництва містить у собі кілька стадій, кожна з яких вносить свою «лепту» у фактичну неоднорідність кінцевого продукту. Одночасне вдосконалення всіх стадій, як правило, занадто трудомістко й дорого. Тому спочатку потрібно з'ясувати, яка зі стадій дає найбільшу неоднорідність, і вдосконалення починати з її. При дослідженні може навіть виявитися, що деякі стадії дають лише незначну неоднорідність, так що витрати на їхнє вдосконалення взагалі були б невиправданими. * Дисперсійний аналіз був вперше розроблений у двадцятих роках ХХ століття англійським статистиком Р.Фішером: (1890-1962). Він призначався спочатку для потреб сільськогосподарської статистики Дисперсійний аналіз у наш час перетворився в потужне знаряддя обробки всіляких спостережень. Він охоплює велике число детально розроблених прийомів планування й обробки експериментів. Основна ідея дисперсійного аналізу полягає в порівнянні дисперсії, породжуваної впливом досліджуваного фактору (факторна дисперсія), і залишкової дисперсії, породжуваної випадковими причинами. Якщо розходження між цими дисперсіями значуще, то фактор впливає на досліджувану величину Х. У цьому випадку середні спостережуваних значень на кожному рівні (групові середні) будуть різнитися також значуще. Для перевірки значущості розходжень дисперсій використовується критерій Фішера. Таким чином, у дисперсійному аналізі порівняння середніх здійснюється через порівняння дисперсій. Якщо встановлено значущість впливу фактору на Х и треба з'ясувати, який з рівнів робить найбільший вплив, то додатково роблять попарне порівняння середніх за допомогою критерія Стьюдента (Стьюдент – псевдонім англійського статистика В.Госсета).
|
|||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 501; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.009 с.) |

 .
. і
і  . З її витягнута вибірка об'єму
. З її витягнута вибірка об'єму  і по ній знайдений коефіцієнт рангової кореляції Спирмена
і по ній знайдений коефіцієнт рангової кореляції Спирмена  . Треба перевірити нульову гіпотезу
. Треба перевірити нульову гіпотезу  про рівність нулю генерального коефіцієнта рангової кореляції при конкуруючій гіпотезі
про рівність нулю генерального коефіцієнта рангової кореляції при конкуруючій гіпотезі  .
. , (2.4.2.1)
, (2.4.2.1) - вибірковий коефіцієнт рангової кореляції Спирмена,
- вибірковий коефіцієнт рангової кореляції Спирмена, - критична точка двосторонньої критичної області.
- критична точка двосторонньої критичної області. .
. , то немає підстав відкинути нульову гіпотезу. Ранговий кореляційний зв'язок між ознаками
, то немає підстав відкинути нульову гіпотезу. Ранговий кореляційний зв'язок між ознаками  , то нульову гіпотезу відкидають, тобто між ознаками
, то нульову гіпотезу відкидають, тобто між ознаками  обчислений коефіцієнт рангової кореляції Спирмена
обчислений коефіцієнт рангової кореляції Спирмена  між оцінками знань студентів по вищій математиці й фізиці. При рівні значущості
між оцінками знань студентів по вищій математиці й фізиці. При рівні значущості  перевірити, чи є значущою рангова кореляція між оцінками по вищій математиці й фізиці.
перевірити, чи є значущою рангова кореляція між оцінками по вищій математиці й фізиці. в таблиці критичних крапок розподілу Стьюдента (додаток 1) знайдемо критичну точку двосторонньої критичної області
в таблиці критичних крапок розподілу Стьюдента (додаток 1) знайдемо критичну точку двосторонньої критичної області 
 .
. , немає підстав відкинути нульову гіпотезу. Інакше кажучи, ранговий кореляційний зв'язок між оцінками по вищій математиці й фізиці незначущий. У той же час такий кореляційний зв'язок, очевидно, повинний існувати. Отриманий результат можна пояснити малим числом спостережень.
, немає підстав відкинути нульову гіпотезу. Інакше кажучи, ранговий кореляційний зв'язок між оцінками по вищій математиці й фізиці незначущий. У той же час такий кореляційний зв'язок, очевидно, повинний існувати. Отриманий результат можна пояснити малим числом спостережень. зв'язана кореляційною залежністю з ознакою Х?
зв'язана кореляційною залежністю з ознакою Х?
 і сукупний коефіцієнт кореляції
і сукупний коефіцієнт кореляції  ?
? і кореляційне відношення
і кореляційне відношення  за даними кореляційної таблиці 30
за даними кореляційної таблиці 30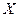


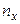
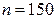


 та
та 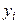 . При рівні значущості 0,05 перевірити, чи значущий знайдений коефіцієнт.
. При рівні значущості 0,05 перевірити, чи значущий знайдений коефіцієнт. . Нульовагіпотеза відкидається; ранговий кореляційний зв'язок значущий.
. Нульовагіпотеза відкидається; ранговий кореляційний зв'язок значущий. , що має
, що має  рівнів
рівнів  Наприклад, якщо потрібно з'ясувати, який вид добрив найбільш ефективний для одержання найбільшого врожаю, то фактор
Наприклад, якщо потрібно з'ясувати, який вид добрив найбільш ефективний для одержання найбільшого врожаю, то фактор  - кількість добрива.
- кількість добрива.


