
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Види залежностей між випадковими величинамиСодержание книги
Поиск на нашем сайте
Головна задача всякого наукового дослідження полягає у вивченні зв'язків між різними явищами. Закони, що відкриваються наукою, являють собою вираження цього зв'язку. Статистика як метод наукового дослідження також повинна бути використана при вивченні зв'язків між явищами. Вчення про математичне вираження деяких видів зв'язку явищ і про прийоми виміру тісноти зв'язків становить одну з найважливіших частин математичної статистики. Як відомо, якщо кожному припустимому значенню однієї величини (аргументу) відповідає одне певне значення іншої величини (функції), то говорять про функціональну залежність між цими величинами. Така залежність виявляється за допомогою строгих логічних доказів, вона не має потреби в дослідній перевірці. Якщо величина Набагато складніше справа з поняттям залежності випадкових величин: якщо при зміні випадкової величини Х змінилася випадкова величина На практиці нерідко виникає помилкова функціональна залежність між випадковими величинами через те, що вплив випадкових факторів, що має місце, слабкіше точності проведених спостережень. У цьому випадку вплив випадкових факторів не може бути враховано, і зв'язок між явищами тільки здається функціональної, хоча такий не є. Як правило, між випадковими величинами існує зв'язок особливого роду, при якій зі зміною однієї величини міняється розподіл іншої. Такий зв'язок називається стохастичним, або ймовірнісним. У математичній статистиці цей зв'язок трансформується, не міняючи своєї суті, у статистичний зв'язок, при якому зі зміною однієї величини змінюється статистичний ряд розподілу іншої. Інакше кажучи, при стохастичному зв'язку значенню однієї випадкової величини відповідає кілька значень іншої, що виникають із певною ймовірністю. При статистичній залежності значенню однієї величини відповідає кілька значень іншої, що мають певні частоти або відносні частоти. Причина такої ситуації полягає в тому, що зміна якого-небудь показника обумовлена змінами іншого показника (показників) не повністю, а частково, оскільки на нього впливають також і інші випадкові фактори. Так, можна без усяких числових даних сказати, що рівень продуктивності праці залежить від рівня його енергооснащеності. Однак продуктивність праці навіть у межах одного великого підприємства, однієї галузі виробництва визначається не тільки енергооснащеністю праці, але й цілим рядом інших факторів. Є підприємства, де рівень енергооснащеності вище, а продуктивність праці нижче середнього рівня. Це означає, що в даному підприємстві на рівень продуктивності праці істотний вплив мали якісь інші фактори (у тому числі й випадкові). Якщо на однакові по площі й по виду ґрунту ділянки сільськогосподарської землі внести однакову кількість тих самих добрив, то врожай, наприклад, зерна не буде однаковим на всіх ділянках. Це пояснюється впливом на врожай цілого ряду випадкових факторів (опади, температура повітря та ін.). Собівартість продукції залежить від продуктивності праці й багатьох інших випадкових факторів. У торгівлі від розміру товарообігу магазина і його спеціалізації залежить цілий ряд якісних показників: вироблення продавця, рівень витрат обігу та ін. Однак ці показники залежать не тільки від зазначених факторів, але й від цілого ряду інших, у тому числі випадкових. При стохастичній залежності зміна випадкової величини Відзначимо ряд особливостей стохастичних (статистичних) зв'язків. 1. У цих залежностях окремі показники жорстко не зв'язані й не входять у якусь єдину систему показників. Так, залежність між енергооснащеністю праці й продуктивністю праці можна виявити, лише порівнюючи розходження цих показників в окремих одиниць сукупності, помічаючи, чи є закономірність у зміні цих розходжень. Інакше кажучи, виражаючись мовою статистики, ці зв'язки пізнаються шляхом порівняння варіацій ознак. Так, розташувавши заводи по зростанню рівня енергооснащеності праці й порівнюючи зміни на цих заводах показника продуктивності праці, можна бачити, чи підтверджується наше припущення про наявність прямого зв'язку в змінах цих показників, чи ні. Або, розташувавши магазини по зростанню товарообігу й порівнюючи в цьому ряді зміни рівня витрат обігу, ми можемо відзначити, чи знижуються рівні витрат у великих магазинах (що ми в праві очікувати), чи ні, тобто, чи є зворотний зв'язок у зміні цих показників. 2. Статистичні зв'язки характеризуються тим, що величина тієї або іншої ознаки змінюється (варіює) під впливом цілого комплексу факторів, деякі з яких мають основне значення для всієї сукупності одиниць (факторів), що ставляться до досліджуваного явища, а інші для всієї сукупності не мають істотного значення, але на окремі фактори можуть дуже впливати. Так, рівень витрат обігу в магазинах залежить не тільки від розміру товарообігу магазина, хоча цей фактор має основне значення для всіх спостережуваних одиниць. На нього впливають і такі фактори, як режим роботи магазина, організація його постачання, умови для зберігання товарів, особисті якості торговельного персоналу й багато інших. Ці "сторонні'' фактори можуть спотворити реальну картину, але якщо взяти для дослідження досить велику кількість магазинів, реальний зв'язок між рівнем витрат обігу й розміром товарообігу виявиться. Це пояснюється тим, що лише в досить великій кількості спостережень впливу факторів, не зв'язаних або слабко пов'язаних із суттю процесу в цілому, взаємно погашаються, нівелюються. Індивідуальні особливості й другорядні фактори відійдуть на другий план і залежність, якщо вона має істотну силу, виявиться досить чітко. Отже, важлива особливість статистичних зв'язків полягає в тому, що вони виявляються не в одиничних випадках, а в масі, і вимагають для свого дослідження досить більшого числа статистичних даних. Помітимо, що перекручуваний вплив, сторонніх причин на досліджувану ознаку повинен носити випадковий характер. Лише при цій умові застосування вироблених математичною статистикою прийомів виміру зв'язків між явищами виявляється правомірним. Математична статистика, що має теоретичною базою теорію ймовірностей, має справу із закономірностями, які виникають у результаті взаємодії великої кількості випадкових впливів. Усяке систематичне перекручування цих закономірностей (воно звичайно пов'язане з неправильним проведенням експерименту в широкому смислі цього слова) повинне бути враховане або усунуте. Інакше можливість використання методів математичної статистики виключається. Окремим випадком статистичного зв'язку є кореляційний зв'язок (від латинського correlatio - співвідношення). Він проявляється в тім, що при зміні однієї величини міняється середнє значень іншої. Уточнимо це поняття. Нехай значенню величини Х = х відповідають п значень величини Умовним середнім
Якщо кожному значенню х відповідає одне значення умовної середньої, то умовна середня є функція від х. Кореляційною залежністю
Аналогічно вводяться умовне середнє
Кореляційною залежністю Х від
Рівняння (1.1.1) називають рівнянням регресії Аналогічне рівняння (1.1.2) – рівняння регресії Х на Якщо між випадковими величинами існує статистичний зв'язок, то це ще не означає, що ці величини зв'язані кореляційно. Але якщо вони зв'язані кореляційно, те між ними завжди існує статистичний зв'язок.
|
||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

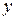 залишається постійної при зміні величини х, то говорять, що
залишається постійної при зміні величини х, то говорять, що  , то ми не можемо відразу сказати, чи є ця зміна результатом залежності від Х, або ця зміна зв'язана лише із впливом випадкових факторів. Правда, і між випадковими величинами може існувати функціональна залежність. Так, випадкова величина
, то ми не можемо відразу сказати, чи є ця зміна результатом залежності від Х, або ця зміна зв'язана лише із впливом випадкових факторів. Правда, і між випадковими величинами може існувати функціональна залежність. Так, випадкова величина 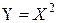 є функція від Х. Або, наприклад, число чоловіків Х и число жінок
є функція від Х. Або, наприклад, число чоловіків Х и число жінок  . Подібного роду залежності між випадковими величинами звичайно відомі з теоретичних міркувань заздалегідь, до всяких спостережень. На практиці вона проявляється в тому випадку, коли для обчислення двох випадкових величин використовуються ті ж самі спостереження (випадок непрямих спостережень), наприклад, при знаходженні числа чоловіків і жінок на 1000 чоловік населення або при обчисленні площі квадрата по обмірюваній стороні. Якщо ж для обчислення кожної з випадкових величин використовуються свої спостереження, то на ці випадкові величини діють різні випадкові фактори й функціональна залежність неможлива. Спробуйте, наприклад, окремо виміряти сторону а квадрата і його площу й ви самі переконаєтеся, що за рахунок випадкових помилок виміру далеко не завжди буде
. Подібного роду залежності між випадковими величинами звичайно відомі з теоретичних міркувань заздалегідь, до всяких спостережень. На практиці вона проявляється в тому випадку, коли для обчислення двох випадкових величин використовуються ті ж самі спостереження (випадок непрямих спостережень), наприклад, при знаходженні числа чоловіків і жінок на 1000 чоловік населення або при обчисленні площі квадрата по обмірюваній стороні. Якщо ж для обчислення кожної з випадкових величин використовуються свої спостереження, то на ці випадкові величини діють різні випадкові фактори й функціональна залежність неможлива. Спробуйте, наприклад, окремо виміряти сторону а квадрата і його площу й ви самі переконаєтеся, що за рахунок випадкових помилок виміру далеко не завжди буде  .
. , що відповідає зміні величини Х, розбивається на дві компоненти. Одна з них пов'язана з реальною залежністю
, що відповідає зміні величини Х, розбивається на дві компоненти. Одна з них пов'язана з реальною залежністю 
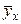 називається середнє арифметичне значень
називається середнє арифметичне значень  .
. . (1.1.1)
. (1.1.1)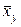 й кореляційна залежність Х від
й кореляційна залежність Х від  .
. . (1.1.2)
. (1.1.2) - регресія Х на
- регресія Х на 


