
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графоаналітичний метод розрахунку нелінійних кілСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В цьому методі струми та напруги в нелінійному колі визначаються за вольт-амперними характеристиками елементів, що входять в це коло. Ці характеристики одержують експериментально або із довідника для стандартних нелінійних елементів: а) При послідовному сполученні нелінійних елементів загальну вольт-амперну характеристику нелінійного кола визначають складанням напруг окремих вольт-амперних характеристик елементів при заданому струмі (рис. 1.53): U = U1+ U2, де U1 – напруга на елементі НЕ1; U2 – напруга на елементі НЕ2; U – напруга, прикладена до еквівалентного НЕ.
Рис. 1.53. До розрахунку НЕ, увімкнених послідовно б) При паралельному сполученні нелінійних елементів загальну вольт-амперну характеристику нелінійного кола одержують складанням струмів окремих вольт-амперних характеристик елементів при заданій напрузі (рис. 1.54): І = І 1 + І 2, де І 1 – струм в елементі НЕЇ; І 2 – в елементі НЕ2; І – струм в нерозгалуженому колі.
Рис. 1.54. До розрахунку кола з НЕ, увімкнених паралельно в) При змішаному сполученні нелінійних елементів спочатку складають вольт-амперні характеристики паралельно увімкнених елементів (як у п .б), а потім послідовно увімкнених (як у п .а):
Це рівняння в координатах и і i представляє і пряму АВ: якщо I = 0, то U 2 = Ε – точка – А, і якщо U 2 = 0, то I = Ε / r 1– точка В. Робоча точка С знаходиться на перетині вольт-амперної характеристики нелінійного елемента та прямої АВ, що визначає рівняння кола. Цю задачу можна розв'язати ще так. Побудувати ΒΑΧ лінійного елемента r (и =ri – пряму лінію, яка проходить через початок координат), а потім задачу розв'язати як в п .а – при послідовному, або як в п. б – при паралельному сполученні. Аналітичний метод розрахунку нелінійних кіл Вольт-амперні характеристики нелінійних елементів іноді вдається апроксимувати аналітичними виразами. Це дає змогу електричний стан нелінійного кола описати математичними рівняннями, розв'язання яких дає числові значення струмів та напруг в нелінійному колі. Один із графоаналітичних методів розрахунку нелінійних кіл полягає в тому, що вольт-амперну характеристику НЕ розділяють на декілька ділянок, і кожну таку ділянку представляють вже прямою лінією. Для кожної із цих ділянок коло розраховують вже як лінійне, що має опір нелінійного елемента r = rд = du / di – на цій ділянці. Потім розрахунки окремих ділянок аналітично стикують, цей метод інколи називають кусково-лінійною апроксимацією вольт-амперної характеристики НЕ. Обидва методи вимагають громіздкого числового розрахунку. Глибше вивчити питання розрахунку нелінійних кіл можна в курсі теоретичної електротехніки або за спеціальною літературою. ЕЛЕКТРИЧНА ЄМНІСТЬ Електрична ємність тіл Нехай маємо відокремлене нерухоме провідне тіло, заряджене до потенціалу φ, яке оточує діелектрик проникністю ε, що не залежить від напруженості поля, тобто в кожній точці середовища є сталою величиною. Тоді заряд такого тіла пропорційний його потенціалу:
Величина С називається електричною ємністю тіла. Отже, електрична ємність відокремленого тіла дорівнює відношенню заряду тіла до його потенціалу. Оскільки значення потенціалу прийнято нульовим на поверхні землі, то φ у (2.1) дорівнює напрузі між землею і заданим відокремленим тілом (рис. 2.1): U = φ – φ3 = φ –0 = = φ. Отже, співвідношення (2.1) можна записати ще так:
де g1, g2… – геометричні величини, які характеризують форму й розміри тіла.
Із визначення (1.14) потенціал на поверхні зарядженої кулі радіуса R дорівнює:
Тоді ємність відокремленої кулі радіуса R визначиться як:
і остаточно C = 4πεR, що підтверджує співвідношення (2.3). За наведеною формулою можна обчислити ємність земної кулі. Середній радіус Землі R = 6380 км, тоді С = 4 ∙ 3,14 ∙ 8,85 · 10-12 · 6380· 103
|
||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 804; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.170.253 (0.008 с.) |




 г) Якщо лінійний елемент r 1сполучений послідовно з нелінійним НЕ (рис. 1.55), то робочу точку С визначають за другим законом Кірхгофа: Ε = U2 + r1I, або U 2 = E – r 1 I, де U 2 – напруга на нелінійному елементі НЕ.
г) Якщо лінійний елемент r 1сполучений послідовно з нелінійним НЕ (рис. 1.55), то робочу точку С визначають за другим законом Кірхгофа: Ε = U2 + r1I, або U 2 = E – r 1 I, де U 2 – напруга на нелінійному елементі НЕ. чи
чи 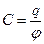


 Розподіл заряду на поверхні відокремленого тіла й картина електричного поля навколо нього залежать від форми тіла. Отже, і потенціал U, і ємність С залежать теж від форми тіла, якщо задана величина заряду q. Якщо тіло оточене однорідним діелектриком електричною проникністю ε, то напруженість електричного поля Ε і, відповідно, потенціал U, при заданому заряді зворотно пропорційні ε діелектрика, що випливає із теореми Гаусса (1.2). На основі цього маємо:
Розподіл заряду на поверхні відокремленого тіла й картина електричного поля навколо нього залежать від форми тіла. Отже, і потенціал U, і ємність С залежать теж від форми тіла, якщо задана величина заряду q. Якщо тіло оточене однорідним діелектриком електричною проникністю ε, то напруженість електричного поля Ε і, відповідно, потенціал U, при заданому заряді зворотно пропорційні ε діелектрика, що випливає із теореми Гаусса (1.2). На основі цього маємо: (2.3)
(2.3) Для прикладу визначимо ємність відокремленої кулі радіуса R. Згідно з теоремою Гаусса напруженість електричного поля відокремленого точкового заряду (1.3)
Для прикладу визначимо ємність відокремленої кулі радіуса R. Згідно з теоремою Гаусса напруженість електричного поля відокремленого точкового заряду (1.3)  . Використаємо цю рівність для одержання потенціалу відокремленого тіла, зарядженого зарядом "+ q " (рис. 2.2). Будемо вважати, що r» R, тоді заряд "+ q " можемо вважати точковим. Тут R – радіус кулі, в центрі якої, вважаємо, знаходиться точковий заряд "+q".
. Використаємо цю рівність для одержання потенціалу відокремленого тіла, зарядженого зарядом "+ q " (рис. 2.2). Будемо вважати, що r» R, тоді заряд "+ q " можемо вважати точковим. Тут R – радіус кулі, в центрі якої, вважаємо, знаходиться точковий заряд "+q".

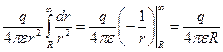 , тут кут
, тут кут 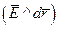 =0°.
=0°.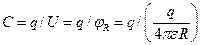
 0,7110-3 Ф.
0,7110-3 Ф.


