
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методи розрахунку електричних кіл постійного струмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Характеристики елементів прийнято називати параметрами кола. В колах постійного струму параметрами елементів є їх опори або провідності. Розглядаючи кола постійного струму, будемо припускати, що параметри всіх елементів кола є величинами сталими, не залежними ні від сили струму в цих елементах, ні від напруг на їх затискачах. Такого роду кола називають лінійними колами, оскільки, застосовуючи до них закони Ома і Кірхгофа, ми одержимо лінійні алгебричні зв'язки між ЕРС, напругами й струмами. Надалі будемо розглядати електричні кола (їх схеми), які складаються з двополюсних елементів. Пригадаємо, що двополюсник – це в загальному випадку послідовне сполучення ЕРС і опору (резистора індуктивності чи ємності), по яких проходить один і той самий електричний струм. Двополюсник теж називають віткою електричного кола. З'єднавши двополюсники у замкнуту систему, утворюємо електричне коло. Простими називають електричні кола, в яких двополюсники (приймачі-опори) сполучені тільки послідовно або тільки паралельно. В іншому випадку кола називають складними чи розгалуженими. Сьогодні існує понад десяток різних методів розрахунку електричних кіл, наприклад, такі, як метод перетворення, метод рівнянь Кірхгофа, метод контурних струмів, метод вузлових напруг, метод накладання, метод еквівалентного генератора тощо. Розглянемо їх окремо для кіл постійного струму. Метод перетворення
Розраховують струми у вітках такої схеми поступовим згортанням схеми, аж поки не одержують найпростішу схему послідовного сполучення ЕРС Е з внутрішнім опором r 0 і еквівалентним опором всієї схеми r E (рис. 1.37). Струм джерела енергії визначається за законом Ома згідно з (1.58): Проілюструємо цей метод на прикладі складної електричної схеми з одним джерелом електричної енергії. Приклад 1.1. Визначити струм у всіх вітках мостової схеми (рис. 1.38).
Задачу розв'яжемо методом перетворення.
Замінимо один із трикутників схеми, наприклад ВСD, еквівалентною зіркою опорами r B, r C, r D (рис. 1.38, б). Для цього використаємо формули (1.71).
Еквівалентний опір ділянки кола АО (рис. 1.38, в) згідно з (1.69) визначається як:
Загальний опір схеми r E (рис. 1.38, г) дорівнює:
Згідно із законом Ома для повного електричного кола (1.58) струм у вітці джерела ЕРС буде:
За схемою (рис. 1.38, в) визначимо спади напруг на опорах:
Струми в опорах r 1 і r 2 визначаються як:
Визначимо напругу на опорах r 3, r 4, r 5. Із схеми (рис. 1.38, б) за другим законом Кірхгофа (вигляду S u, е=0) маємо:
звідси U BC = U B + U C = 38,4 + 24 = 62,4 В; U DC = U D + U C = 28,4 + 24 = 52,8 В; U BD = U B + U D = 38,4 – 28,8 = 9,6 В; де U B = r B× I 1 = 12 × 3,2 = 38,4 В; U D = r D× I 1 = 36 × 0,8 = 28,8 В; Струми в опорах r 3, r 4, r 5 будуть дорівнювати:
Перевірка. За першим законом Кірхгофа для вузла С і В маємо: I 4 + I 5 = I 6 => 3,12 + 0,88 = 4 А; I 4 + I 3 = I 1 => 3,12 + 0,8 = 3,2 А; За другим законом Кірхгофа для замкненого контуру (рис. 1.38, в): U C + U AD + U 6 = Е => 24 + 64 + 32 = 120 В.
Метод рівнянь Кірхгофа В цьому методі розглядаються складні електричні кола, особливо такі, в яких діють дві або більше ЕРС, увімкнені у різні вітки схеми. Розв'язання таких задач методом перетворення достатньо складне, а в деяких випадках, й неможливе. Пропонований нижче метод рівнянь Кірхгофа дає змогу розв'язувати як завгодно складні електричні схеми без їх трансфігурацій.
Оскільки схема має р віток, то невідомих струмів у схемі буде теж p і для їх розрахунку треба скласти p рівнянь. За першим законом Кірхгофа (S I = 0) можемо скласти q –1 лінійно незалежних рівнянь (на одиницю менше ніж вузлів). Застосовуючи другий закон Кірхгофа

Отже, за законами Кірхгофа можна скласти (q – 1)+(q – 1)+ p – (q –1) = р рівнянь. А це означає, що кількість рівнянь буде дорівнювати кількості невідомих струмів (р) у вітках схеми. Розв'язавши сумісно ці рівняння, одержимо числові значення струмів віток схеми. Послідовність проведення розрахунку така: 1) для заданої електричної схеми визначаємо кількість вузлів (q), віток (р) і контурів (n); 2) вибираємо умовно-додатні напрямки струмів у вітках схеми (довільно); 3) за першим законом Кірхгофа складаємо (q – 1) рівнянь, а за другим законом n рівнянь; рекомендується для всіх контурів вибирати однакові додатні напрямки їх обходу, наприклад, всі за годинниковою стрілкою (чи проти); 4) сумісно розв'язуємо складену систему рівнянь і одержуємо числові значення струмів віток. Якщо в результаті розрахунку кола які-небудь струми будуть виражені від'ємними числами, то це означає, що напрям руху додатних зарядів спрямовані протилежно вибраним умовно-додатним напрямам струмів цих віток. Напрямлення стрілок струмів цих віток змінювати не треба. Розрахунок електричних кіл методом рівнянь Кірхгофа є основним. За допомогою цього методу можна розрахувати будь-яке електричне коло. Однак цей метод громіздкий, тому що вимагає розв'язування системи з кількістю рівнянь, що дорівнює кількості віток кола. Всі інші методи, які застосовуються для розрахунку електричних кіл, базуються на законі Ома і законах Кірхгофа. Баланс потужності в електричному колі. В § 1.9 формулою (1.49) був виражений баланс потужності в електричній схемі, яка складалась з послідовного сполучення Е, r 0 та R 11. Якщо електричне схема має р віток, в кожній вітці є резистивний опір r, джерело ЕРС Е з внутрішнім опором r0, то баланс потужності в такій схемі визначається виразом:
де Е К І К – потужність генератора (джерела електроенергії) k -і вітки; r 0k I k2 – потужність, яка витрачається на внутрішньому опорі самого генератора; r k I k2 – потужність, яка виділяється в опорі r к k -ї вітки. Компоненти Е k І k можуть бути як додатними, так і від'ємними. Якщо Е к І к>0 то відповідні джерела ЕРС працюють у режимі генераторів, а якщо Е к І к<0 – то в режимі приймачів електричної енергії. Розрахунок складного електричного кола за методом рівнянь Кірхгофа проілюструємо на прикладі. Приклад 1.2. Розрахувати струми у всіх вітках електричного кола, схема якого наведена на рис. 1.42. Параметри елементів електричного кола мають такі значення: Е = 50 В, r 01 = 2 Ом, r 1 = 18 Ом, Е 2 = 20 В, r 02 = 1 Ом, r 2 = 9 Ом, r 3 = 30 Ом, r 4= 40 Ом, Е 5 = 100 В; r 05=2Ом, r 5 =48 Ом, r б=30 Ом, E 7 = 50 В, r 07 =0, r 7 = 10 Ом. 1. Визначимо кількість вузлів, віток і контурів: q = 4, р = 1, n = 4. 2. Довільно вибираємо і позначаємо на схемі умовно-додатні напрями струмів у вітках.
3. Складаємо q -1 = 4-1 = 3 рівняння за першим законом Кірхгофа (для вузлів 1, 2, 3), та n =4 рівняння за другим законом Кірхгофа для контурів I-IV, прийнявши додатні напрямки обходу контурів за годинниковою стрілкою: 1. – I 1– I 2+ I 5=0 2. I 1+ I 2– I 3– I 4=0 3. I 3+ I 6+ I 7=0 4. (r 1+ r 10) I 1–(r 2+ r 20) I 2= E 1– E 2 5. (r 2+ r 20) I 2+ r 4 I 4+(r 05+ r 5) I 5= E 2– E 5 6. r 3 I 3– r 4 I 4– r 6 I 6=0 7. r 6 I 6–(r 7+ r 07) I 7= – E 7 В систему рівнянь (1...7) підставимо числові значення величин Е, r 0 та r. 1. – I 1– I 2+ I 5=0 2. I 1+ I 2– I 3– I 4=0 3. I 3+ I 6+ I 7=0 4. (18+2) I 1–(9+1) I 2=50-20 5. (9+1) I 2+40 I 4+(48+2) I 5=20-100 6. 30 I 3–30 I 6–40 I 4=0 7. 30 I 6–(0+10) I 7=50 Розв'язавши цю систему рівнянь, одержимо числові значення струмів віток схеми: I 1=0,608 А; I 2 = -1,783 А; I 3 = -1,090 А; I 4 =-0,084 A; I 5 = -1,175А; I 6 = -0,977А; I 7 = 2,067 А. Струми I 1 та I 7 (зі знаком "плюс") в електричному колі мають таке спрямування, яке позначено на схемі, а решта струмів (зі знаком "мінус") мають в електричній схемі протилежне спрямування (напрями стрілок змінювати не треба). За формулою (1.73) складемо баланс потужностей. Потужність джерел електричної енергії:
Потужність, яка витрачається в опорах віток схеми:
Отже, 216,671 – 6,684 = 208,987 Вт, що дорівнює потужності, яку генератори ЕРС виділяють в опорах схеми. Збігання числових даних підтверджує правильність розв'язання задачі.
Метод контурних струмів Метод рівнянь Кірхгофа, хоча й простий за складанням самої системи рівнянь, але громіздкий за обчислювальною роботою – вимагає розв'язання системи із великої кількості (р) рівнянь. Запропонований Дж. К. Максвеллом метод контурних струмів для розрахунку електричних кіл з постійними параметрами зводиться до розв'язання системи тільки з " n " рівнянь. В цьому методі вводяться нові невідомі, контурні струми. Кількість їх дорівнює кількості лінійно незалежних контурів схеми (n). Метод контурних струмів більш економічний за обчислювальною роботою (має меншу кількість рівнянь), ніж метод рівнянь Кірхгофа. Виведення основних розрахункових рівнянь наведемо на основі скелетної схеми, зображеної на рис. 1.42. Контурні струми за значенням вибираємо такими, щоби струм в будь-якій вітці схеми визначався алгебричною сумою контурних струмів, які протікають через цю вітку. Для схеми рис. 1.42. струми віток будуть такими:
Розпочинаючи складання рівнянь для кола з п лінійно незалежними контурами, задаємось довільно додатними напрямками контурних струмів у всіх контурах, і домовимось за додатний напрям обходу контуру вибирати напрям, який збігається з його контурним струмом.
де E 11 – сума всіх ЕРС, які входять в перший контур. Визначаючи цю суму, EРС, напрям яких збігається з напрямом обходу контуру, треба брати зі знаком ''плюс", а ті, що не збігається – зі знаком "мінус". Підставивши (1.74) в (1.75) і звівши подібні члени, одержимо рівняння для першого контуру, виражене через контурні струми:
Введемо позначення: r kk – сума всіх опорів, які входять в к-й контур його називають власним опором k- го контуру; r km = r mk – сума всіх опорів у загальній (спільній) вітці k- гой т- гоконтуру, його називають взаємним опором k- го та m- го контурів. Простежимо послідовність складання рівняння (1.76) безпосередньо за схемою: перший доданок (r 1+ r 10+ r 7) I k1 є сумою спадів напруг на власних опорах першого контуру, які виникають під дією першого контурного струму I К1; другий доданок (- r 10 I k2) ураховує спад напруг на спільному опорі першого та другого контурів, і викликаного струмом другого контуру, а знак «мінус» ураховує, що струми I К2 та I k1 в опорі r 10спрямовані зустрічне; третій доданок ураховує спад напруг на опорі r 7, викликаний струмом I K6(- r 7 I K6)а знак «мінус» ураховує, що струми I K6 та I K1 в опорі r 7 теж напрямлені зустрічне. Отже, рівняння для останніх контурів схеми (рис. 1.42) можуть бути записані аналогічно рівнянню (1.76):
Систему рівнянь (1.76-1.77) можна записати в загальному вигляді для будь-якої схеми, яка має п контурів:
У системі рівнянь (1.78) за додатний напрям обходу к- r o контуру прийнято його контурний струм I Km, тому складові (r 11 I K1, r 22 I K2, …, r nn I Kn)матимуть знак "плюс". Якщо всі контурні струми кола напрямлені однаково (за годинниковою стрілкою чи проти, а так рекомендується спрямовувати), то останні складові r ms I ks ( Послідовність проведення розрахунку така: 1) для заданої електричної схеми визначаємо q, p, п; 2) вибираємо додатні напрями контурних струмів і записуємо для них систему з п рівнянь (1.78); 3) розв'язуємо цю систему рівнянь і знаходимо числові значення контурних струмів: I k1, I k2,…, I kn, 4) позначаємо умовно додатні напрямки струмів у вітках схеми та знаходимо їх як алгебричну суму контурних струмів, що протікають через цю вітку; 5) перевіряємо правильність розв'язання задачі за другим законом Кірхгофа Приклад 1.3. Застосування методу контурних струмів для розрахунку струмів у електричному колі з постійними параметрами покажемо на схемі, зображеній на рис. 1.41. Схема має чотири контури (n = 4), а отже, і чотири контурні струми. Додатні напрями контурних струмів за годинниковою стрілкою. Система рівнянь, складених для контурних струмів, згідно із (1.78), буде такою:
1. (r 1+ r 01+ r 2+ r 02) I k1–(r 2+ r 02) I k2= E 1– E 2 2. (r 2+ r 02+ r 4+ r 5+ r 05) I k2–(r 2+ r 02) I k1– r 4 I k3= E 2– E 5 3. (r 3+ r 6+ r 4) I k3– r 4 I k2– r 6 I k4=0 4. (r 6+ r 7+ r 07) I k4– r 6 I k3= – E 7 Підставимо числові дані величин r 0, r, E: 1. (18 + 2 + 9 + l) I kl – (9 + 1) I k2 = 50 – 20; 2. (9 + 1 + 40 + 48 + 2) I k2 – (9 + 1) I k1 – 40 I k3 = 20 – 100; 3. (39 + 30 + 40) I k3 – 40 I k2 – 30 I k4 = 0; 4. (30 + 50 + 0) I k4 – 30 I K3 = – 50. Розв'язавши цю систему рівнянь відносно значень контурних струмів I k1… I k4, отримаємо: I k1=0,608 A; I k2=-1,176 A; I k3=-1,091 A; I k4=-2,068 A; Позначимо додатні напрямки струмів у вітках схеми й визначимо їх значення через контурні струми: I 1= I k1=0,608 A; I 2= I k2– I k1=-1,176–0,608 Ф=-1,784; I 3= I k3=-1,091 А; I 4= I k2– I k3=-1,176–(-1,091)=-0,085 А; I 5= I k2=-1,176А; I 6= I k4– I k3=-2,068–(–1,091)=-0,977 А; I 7= – I k1= –(–2,068)=2,068 A. Перевірка. За другим законом Кірхгофа ( (r 1+ r 01) I 1–(r 2+ r 021) I 2= E 1– E 2 і в цифрах: (18+2) R 6 I 6-(r 7+ r 07) I 7=- E 7 і в цифрах: -0,977 Метод вузлових напруг За методом вузлових напруг кількість рівнянь можна скоротити до (q – 1). Отже, метод вузлових напруг (його ще називають метод вузлових потенціалів) найраціональніше використовувати для електричних схем з малою кількістю вузлів, а метод контурних струмів – з малою кількістю контурів (чи віток). Покажемо суть цього методу (рис. 1.43, a). Уявно один вузол схеми завжди можна заземлити, від цього розподіл струмів у вітках не зміниться. Потенціал заземленого вузла стане дорівнювати нулеві. Заземливши четвертий вузол, отримаємо: 1-4: 2-4: 3-4: Як видно з останніх виразів, вузлові напруги (UB1, UB2, UB3) дорівнюють відповідним потенціалам вузлів (
Аналогічно, обходячи контури за напрямом струмів віток і по вузлових напругах, одержимо значення інших струмів:
За першим законом Кірхгофа запишемо рівняння струмів для вузла №1: I 1+ I 2– I 3+ I 6=0 В останнє рівняння підставимо значення струмів (1.79), виражених через вузлові напруги:
Після згрупування подібних членів останнє рівняння запишеться так:
Отже, ліва частина рівнянь (1.80) записується так: вузлова напруга вузла UBm множиться на суму провідностей віток, які приєднані до т- говузла, мінус вузлова напруга сусіднього вузла (U Bk)помноженої на суму провідностей віток, що безпосередньо з'єднують m -й та k- йвузли, мінус UB(k+1) і т.д. Права частина кожного із рівнянь (1.80) дорівнює алгебричній сумі добутків ЕРС кожної вітки, приєднаної до розглянутого вузла, на її провідність. Добуток Eg записується з додатним знаком, якщо ЕРС напрямлена до вузла, для якого записується рівняння, та з від'ємним – якщо ЕРС напрямлена від вузла. Введемо такі позначення: G11=g1+ g2+ g3+ g6= G22=g3+ g4+ g5+ g6= G33=g4+ g5+ g7=
Або в загальному вигляді для схеми, яка має g вузлів, рівнянь буде (q – 1):
Кількість невідомих у методі вузлових напруг дорівнює кількості рівнянь, які треба скласти для схеми за першим законом Кірхгофа (q -1). Метод вузлових напруг, як і метод контурних струмів, є одним із основних розрахункових прийомів. В тому випадку, коли (q -1) < n, цей метод є більш економічний, ніж метод контурних струмів, n – кількість незалежних контурів схеми. Послідовність проведення розрахунку. Для схеми визначаємо q, р, n. Один із вузлів схеми подумки заземлюємо (нехай його потенціал дорівнює нулеві). Позначимо вузлові напруги на схемі, їх будемо мати (q – 1). Згідно з (1.81) складаємо систему (q - 1) рівнянь, відносно вузлових напруг U B1, U B2..., U B(q-1). Розв’язавши цю систему рівнянь, одержуємо числові значення вузлових напруг U B1, U B2, U B(q-1).Позначаємо струми у вітках і за законом Ома аналогічно (1.79), обходимо контури за напрямом струму вітки й за вузловими напругами – визначаємо струми віток схеми.
Приклад 1.4. За методом вузлових напруг визначити струми в схемі, зображеній на рис. 1.44. Параметри схеми такі:
Розв'язання. Для схеми маємо р = 5, q = З, п = 3, отже q- 1< п, що доцільно задачу розв'язувати за методом вузлових напруг. Опір першої вітки дорівнює нулеві, тому за базисний вузол (потенціал якого буде дорівнювати нулеві) бажано взяти вузол "1" або "3". Приймаємо 1. U B1– E 1=0 2. Підставимо числові значення 1. U B1-100=0 2. Розв'язавши ці рівняння, одержимо UB1= 100 В, UB2 = 33,33 В. Тоді струми віток:
Струм І 1 знаходимо за першим законом Кірхгофа для вузла "1": I 1+ I 2– I 5=0, звідки, I 1= I 5– I 2=3,33–(–5)=8,33 А Перевіримо за другим законом Кірхгофа для другої вітки: U BI+ U 2– E 2= 0 => 100 + (– 5)10 – 50 = 0. Тотожність зберігається, що підтверджує правильність розв'язування задачі.
|
|||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 2479; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.104.48 (0.012 с.) |


 Метод перетворення застосовується для розрахунку електричних кіл з одним джерелом електричної енергії.
Метод перетворення застосовується для розрахунку електричних кіл з одним джерелом електричної енергії. , а струм k -ї вітки (k -го приймача електроенергії) буде дорівнювати:
, а струм k -ї вітки (k -го приймача електроенергії) буде дорівнювати:  , де U к- напруга між вузлами, до яких приєднана k -та вітка; r k – опір k -ї вітки.
, де U к- напруга між вузлами, до яких приєднана k -та вітка; r k – опір k -ї вітки.
 r 1 = 8 Ом; r 2 = 44 Ом; r 3= 120 Ом, r 4 = 20 Ом, r 5 = 60 Ом, r 6 = 8 Ом; E =120 В.
r 1 = 8 Ом; r 2 = 44 Ом; r 3= 120 Ом, r 4 = 20 Ом, r 5 = 60 Ом, r 6 = 8 Ом; E =120 В.




 ;
; 




 Нехай складне коло складається з р віток, має q вузлів (рис. 1.39) і кількість контурів n = р – (q – 1). Як правило, для електричних схем відомі параметри віток – їх опори, та значення і напрямки діючих в схемі ЕРС. Розрахунок буде зводитися до розрахунку значень струмів у вітках схеми, хоча завдання може ставитися й по-іншому.
Нехай складне коло складається з р віток, має q вузлів (рис. 1.39) і кількість контурів n = р – (q – 1). Як правило, для електричних схем відомі параметри віток – їх опори, та значення і напрямки діючих в схемі ЕРС. Розрахунок буде зводитися до розрахунку значень струмів у вітках схеми, хоча завдання може ставитися й по-іншому. , можна скласти стільки рівнянь, скільки лінійно незалежних замкнутих контурів (n) має схема. Для незалежності рівнянь або, як кажуть, для незалежності контурів, ці контури необхідно вибирати так, щоб кожен наступний контур відрізнявся від попередніх, принаймні однією новою віткою. Ця умова є достатньою, але не завжди необхідною. Наприклад, якщо розглянути схеми (рис. 1.40) і вибирати контури в такій послідовності, як показано на схемах, то всі вітки для контурів: 3-у схемі (а), 4-у схемі (б) та 5 – у схемі (в) вже увійшли в рівняння попередніх контурів, але кількість рівнянь для контурів цих схем ще буде недостатньою. В таких випадках недостатню кількість рівнянь за другим законом Кірхгофа складають для контурів, всі вітки яких уже увійшли в попередні контури. Отже, критерієм визначення кількості лінійно незалежних контурів є співвідношення n = р – (q – 1).
, можна скласти стільки рівнянь, скільки лінійно незалежних замкнутих контурів (n) має схема. Для незалежності рівнянь або, як кажуть, для незалежності контурів, ці контури необхідно вибирати так, щоб кожен наступний контур відрізнявся від попередніх, принаймні однією новою віткою. Ця умова є достатньою, але не завжди необхідною. Наприклад, якщо розглянути схеми (рис. 1.40) і вибирати контури в такій послідовності, як показано на схемах, то всі вітки для контурів: 3-у схемі (а), 4-у схемі (б) та 5 – у схемі (в) вже увійшли в рівняння попередніх контурів, але кількість рівнянь для контурів цих схем ще буде недостатньою. В таких випадках недостатню кількість рівнянь за другим законом Кірхгофа складають для контурів, всі вітки яких уже увійшли в попередні контури. Отже, критерієм визначення кількості лінійно незалежних контурів є співвідношення n = р – (q – 1).

 Втрати потужності в самих джерелах електроенергії:
Втрати потужності в самих джерелах електроенергії:


 де I к1, I K2 ,…, I k6 – контурні струми.
де I к1, I K2 ,…, I k6 – контурні струми. Для першого контуру запишемо рівняння за другим законом Кірхгофа (
Для першого контуру запишемо рівняння за другим законом Кірхгофа ( ):
):
 )в системі рівнянь (1.78) виступатимуть із знаком "мінус", тому що контурний струм I ks в опорі rms завжди буде напрямлений зустрічне контурному струму I km, напрям якого вибрано за додатний напрям обходу m -го контуру.
)в системі рівнянь (1.78) виступатимуть із знаком "мінус", тому що контурний струм I ks в опорі rms завжди буде напрямлений зустрічне контурному струму I km, напрям якого вибрано за додатний напрям обходу m -го контуру.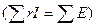 для контурів схеми.
для контурів схеми.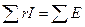 ) проведемо перевірку для будь-яких контурів, наприклад, для першого та четвертого.
) проведемо перевірку для будь-яких контурів, наприклад, для першого та четвертого. 0,608–(9+1)
0,608–(9+1)  . Тоді напруги між вузлами будуть дорівнювати:
. Тоді напруги між вузлами будуть дорівнювати:

 ), тому пропонований спосіб розрахунку ще називають методом вузлових потенціалів.
), тому пропонований спосіб розрахунку ще називають методом вузлових потенціалів. Виразимо струми віток схеми через вузлові напруги. Для цього виділимо одну вітку схеми, наприклад третю (рис. 1.43, б), і виразимо її струм I3 через відповідні напруги. За другим законом Кірхгора (
Виразимо струми віток схеми через вузлові напруги. Для цього виділимо одну вітку схеми, наприклад третю (рис. 1.43, б), і виразимо її струм I3 через відповідні напруги. За другим законом Кірхгора ( )для замкненого контуру маємо:
)для замкненого контуру маємо: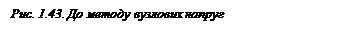
 , чи
, чи  , звідкіля
, звідкіля
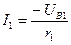

 ………..
………..




 ;
; ;
; – це сума провідностей віток, приєднаних відповідно до 1-го, 2-го та 3-го вузлів.
– це сума провідностей віток, приєднаних відповідно до 1-го, 2-го та 3-го вузлів. ,
,  – це сума провідностей віток, які з’єднують 1 і 2 та 2 і 3 вузли. Тоді рівняння (1.80) з врахуванням наведених позначень запишуться так:
– це сума провідностей віток, які з’єднують 1 і 2 та 2 і 3 вузли. Тоді рівняння (1.80) з врахуванням наведених позначень запишуться так:



 Застереження. Коли у вітці схеми увімкнене ідеальне джерело ЕРС (без внутрішнього опору) і сама вітка теж немає опору, то тоді за базисний вузол (
Застереження. Коли у вітці схеми увімкнене ідеальне джерело ЕРС (без внутрішнього опору) і сама вітка теж немає опору, то тоді за базисний вузол ( = 0) бажано вибирати один із вузлів, до якого приєднана ця вітка. У противному разі одне із рівнянь (1.81) перетворюється у невизначеність й потрібно буде її находити, що наочно буде видно із наведеного нижче прикладу.
= 0) бажано вибирати один із вузлів, до якого приєднана ця вітка. У противному разі одне із рівнянь (1.81) перетворюється у невизначеність й потрібно буде її находити, що наочно буде видно із наведеного нижче прикладу. E1 = 100 В; Е2 = 50 В; Е3 = 50 В; r 2 = 10 Ом; r 3 = 5 Ом; r 4 = r 5 = 20 Ом
E1 = 100 В; Е2 = 50 В; Е3 = 50 В; r 2 = 10 Ом; r 3 = 5 Ом; r 4 = r 5 = 20 Ом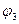 = 0. Позначимо вузлові напруги UB1 та UB2 і складемо систему двох рівнянь [ (q – 1) = 3 – 1= 2]:
= 0. Позначимо вузлові напруги UB1 та UB2 і складемо систему двох рівнянь [ (q – 1) = 3 – 1= 2]: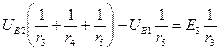

 ;
; 
 ;
; 



