
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Резистивний, індуктивний та ємнісний опори в колі синусоїдного струмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
У загальному випадку електричне коло змінного струму може мати резистивні (r), індуктивні (L) та ємнісні (С) елементи. У колах постійного струму індуктивний і ємнісний елементи проявляють себе в моменти увімкнення чи вимкнення кола та під час зміни параметрів схеми, коли змінюється струм і проявляється ЕРС самоіндукції В усталених режимах кіл постійного струму струм не змінюється і тому напруга на котушці У колах змінного струму безперервно змінюється струм, в результаті чого виникає напруга на котушці та струм в конденсаторі, які змінюються в часі. Розглянемо окремо ці елементи (опори) вколі змінного струму.
Миттєве значення струму в колі згідно з законом Ома буде:
Розділивши ліву і праву сторони останньої рівності на
Із виразів (4.10) та (4.11) випливає, що струм і напруга на резистивному опорі збігаються за фазою; кут зсуву фаз між струмом та напругою На рис. 4.8, б зображені часові залежності напруги, струму та миттєвої потужності s(t), а на рис. 4.8, в наведена векторна діаграма напруги та струму в резистивному опорі. Миттєве значення потужності визначається добутком миттєвого значення напруги на миттєве значення струму:
Як видно із (4.13) та з часової діаграми (рис. 4.8, б), потужність s (t)в резистивному опорі змінюється від нуля до Sm і залишається завжди додатною. Це означає, що в колі з резистивним опором потужність (енергія) увесь час надходить із мережі до споживача r і незворотно перетворюється в інші види (енергії. Визначимо середнє значення потужності за період
підставивши U = rI, одержимо:
Отже, активна потужність у резистивному опорі r перетворюється в тепло.
Під дією синусоїдної напруги струм у котушці теж буде синусоїдним:
Напруга на котушці є такою:
де Розділивши ліву і праву частини останнього виразу на
де Із виразів (4.15) і (4.16) випливає, що напруга на котушці випереджує за фазою струм на 90° або струм відстає від напруги на 90°. Кут зсуву фаз між струмом і напругою котушки є a На рис. 4.9, б зображено часові залежності напруги, струму та миттєвої потужності s(t), а на рис. 4.9, в наведена векторна діаграма напруги, струму та ЕРС самоіндукції EL котушки індуктивності. Миттєве значення потужності s (i)в колі з індуктивністю є:
а середнє значення цієї потужності за період (активна потужність) дорівнює нулеві:
Для з'ясування енергетичних процесів у колі з індуктивністю використаємо часові залежності миттєвих значень u, і, s (t)(рис. 4.9, б). В інтервалі часу від t = 0 (точка 1) до t = 1/4 T (точка 2), коли струм в колі зростає від 0 до I m електрична енергія з мережі надходить в індуктивність (s (t) > 0) і нагромаджується в ній у вигляді енергії магнітного поля. Найбільше значення цієї енергії є при максимальному струмі (3.37): Отже, в колі з індуктивністю наявний неперервний періодичний процес обміну енергією між електричною мережею (джерелом електроенергії) і магнітним полем індуктивності. Цю енергію називають реактивною енергією і, відповідно, потужність – реактивною потужністю. Отже, миттєве значення; потужності s (t), що підходить до ідеальної котушки (rк = 0), – це миттєве значення реактивної потужності q(t), а максимальне її значення (qm) називають реактивною потужністю Q.
Як правило, реальна котушка, крім індуктивності L, має ще резистивний опір r к. Цей опір зумовлений присутністю самого опору провідника котушки; Конденсатор С. Ємнісний опір Нехай до ідеального (без втрат) конденсатора (рис. 4.11, а) прикладена синусоїдна напруга:
Тоді струм в конденсаторі знайдемо із співвідношення
чи
де
Поділимо ліву і праву сторону останнього виразу на
де хс – ємнісний опір; Із виразів (4.19) і (4.21) видно, що струм конденсатора випереджує за фазою напругу на 90° або напруга відстає від струму на 90°. Кут зсуву фаз між напругою і струмом в конденсаторі: На рис. 4.11, б зображені часові залежності напруги, струму та миттєвої потужності, а на рис. 4.11, в наведена векторна діаграма напруги й струму ідеального конденсатора. Миттєве значення потужності s (t)в колі з конденсатором:
а її середнє значення за період (активна потужність) дорівнює нулеві:
Для з'ясування енергетичних процесів у колі з конденсатором використаємо часові залежності миттєвих значень (рис. 4.11, б). У першу чверть періоду між точками 1 і 2 напруга на конденсаторі зростає, конденсатор заряджається, електрична енергія з мережі надходить в конденсатор (s (t) > 0) і нагромаджується у формі енергії електричного поля (2.14): Отже, у колі з конденсатором, так само, як і в колі з індуктивністю, відбувається неперервний періодичний обмін енергії між мережею та конденсатором. Потужність, що характеризує швидкість зміни цієї енергії, теж називається реактивною потужністю. Отже, реактивна енергія (потужність) коливається між джерелом електричної енергії і споживачем (не виходить з електричної мережі) і йде на утворення магнетних полів у котушках і електричних полів у конденсаторах. На рис. 4.11, в зображена векторна діаграма напруги й струму ідеального конденсатора. Параметри недосконалого конденсатора. При змінній напрузі в конденсаторах з твердими або рідкими діелектриками, на відміну від повітряних конденсаторів, частина підведеної до них енергії тратиться на поляризацію діелектрика за рахунок струму зміщення
Недосконалий конденсатор можна замінити еквівалентною послідовною чи паралельною схемами з відповідними величинами Параметри (
а параметри
Необхідно зауважити, що
Відміна між значеннями тим більша, чим більший, тангенс кута втрат
Тангенс кута втрат не залежить від схеми за якою проводилось вимірювання і розрахунок:
Значення На практиці основними параметрами конденсатора є його ємність, напруга й кут втрат (С, U, 4.4. Послідовне з'єднання резистивного, індуктивного та ємнісного опорів у колі синусоїдного струму. Закон Ома в класичній формі. Трикутник опорів. Коефіцієнт потужності cos φ До кола (рис. 4.13, а) прикладена синусоїдна напруга:
Струм у колі теж буде синусоїдним і =І m sin(ω t + ψ i). Для спрощення викладення підберемо таку початкову фазу напруги (ψ u), Щоб початкова фаза струму дорівнювала нулеві: ψ i = 0; початкова фаза напруги тоді буде ψ u = φ, (φ = ψ u – ψi = ψ u – 0 = ψ u). Тоді буде мати:
Рис. 4.13. Послідовне з’єднання r, L, С (а), векторна діаграма (б) та трикутник опорів (в) Запишемо рівняння за другим законом Кірхгофа для миттєвих значень (рис. 4.13 ,а): u = ur + ul +uc Виразивши напруги через струм і опори ділянок кола, одержимо:
або
На основі рівняння (4.26) побудуємо векторну діаграму для діючих значень напруг (рис. 4.13, б). Вектор напруги
а його величина
Виразивши в (4.27) напруги через струм і опори, одержимо:
Звідси
де
Співвідношення (4.28) – це закон Ома, записаний в класичній формі: тут U та І – діючі значення напруги та струму; z – повний опір кола, Ом; x – реактивний опір кола, Ом. Поділивши сторони трикутника напруг (рис. 4.13, б) на діюче значення струму І, одержимо трикутник опорів (рис. 4.13, в). Із трикутника опорів визначимо коефіцієнт потужності схеми cos φ
Детальніше про цю величину мова піде нижче.
4.5. Потужність в колі послідовного з'єднання резистивного r і реактивного x опорів До схеми (рис. 4.14, а) прикладемо синусоїдну напругу и = Umsin(ωt + φ) і в колі матимемо струм і = I msin ω t. Напруга зсунута відносно струму на кут φ, який визначається із трикутника опорів (рис. 4.13, в): φ = arctg(x / r) = arctg((xL – x C) / r). Якщо xL > xC, тоді φ > 0 і напруга випереджує струм за фазою; якщо xL < xC тоді φ < 0 і напруга відстає від струму. Якщо xL = xC,φ = 0, напруга збігається за фазою зі струмом. На рис. 4.14, б наведені часові залежності u (t) та i (t)для φ>0. Миттєве значення потужності: s (t) = и і = Um sin(ω t+ φ) · Іт sin ω t = 2UI sin ω t (sin ω t cos φ+cos ωtsin φ) = =
Рис. 4.14. Потужності p(t), q(t), s(t) в колі з опором r-х чи
Перша складова виразу (4.32) – це миттєве значення активної потужності p(t), а друга складова – реактивної q (t):
На рис. 4.14 ,в,г,д показані часові залежності миттєвих величин потужностей, відповідно, повної s (t), активної p (t)та реактивної q (t). Амплітуда реактивної потужності є величиною, яку в колах синусоїдного струму називають реактивною потужністю, отже:
Визначимо середнє значення потужності за період – активну потужність:
Інтеграл другої складової виразу (4.34) дорівнює нулеві. Піднесемо до квадрата вирази (4.33) та (4.34) і додамо:
звідки Ρ 2 + Q 2 = (UI) 2 = S 2. Величину добутку U ∙ І називають повною або позірною потужністю S, а трикутник (рис. 4.14, е) – трикутником потужностей. Отже, формули для визначення активної, реактивної та повної потужностей є такими:
Наведені потужності можуть бути теж розраховані за діючим значенням струму й відповідного опору за такими формулами:
Одиниці вимірювання: [ S ] = 1 ΒΑ, 1 кВА; [ Ρ ]= 1 Вт, 1кВт; [ Q ] = 1 ВАр, 1 кВАр. Повна (позірна) S і активна Ρ потужності завжди додатні. Якщо φ > 0 (резистивно індуктивні кола) – реактивна потужність Q додатна, а якщо φ < 0 (резистивно ємнісні кола) Q – від’ємна. Повна потужність S характеризує найбільше значення середньої потужності (активної), яку можна одержати в колі за заданих діючих значень напруги та струму (тобто якщо φ = 0, cos φ = 1). Із трикутника потужностей коефіцієнт потужності може бути визначений як:
Приклад 4.2. Електричне коло послідовно сполучених резистивного опору r = 10 Ом, індуктивності L = 50 мГн і ємності С = 1000 мкФ, приєднане до електричної мережі синусоїдної напруги з діючим значенням 220 В і частотою 50 Гц (рис. 4.13, а). Вичислити повний опір кола z, cos φ, діюче значення струму, напруги на елементах кола, потужності активну, реактивну й позірну та побудувати векторну діаграму.
Розв'язання. Резистивний опір схеми r = 10 Ом. Індуктивний опір Ємнісний опір Повний опір схеми Коефіцієнт потужності:
Діюче значення струму І = U/z = 220/ 16= 13,8 A Діючі значення напруг: на резистивному опорі Ur= rІ= 13,8 · 10 = 138 В, на котушці UL = хLI = 13,8 · 15,7 = 216 В на ємності UC = хCI = 13,8 ∙ 3,18 = 44 В. Повне діюче значення напруги
Потужності: активна Ρ = UIcos φ = 220 · 13,8 · 0,625 = 1900 Βт = 1,9 κΒт; реактивна Q = UIsin φ = 220 · 13,8 ∙ 0,81 = 2380 ВАр = 2,38 кВАр; повна S = UI = 220 · 13,8 = 3040 ВА = 3,04 кВА. Векторна діаграма буде аналогічною діаграмі зображеній на рис. 4.13, б.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1662; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.88.16 (0.013 с.) |

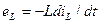 та ЕРС ємності
та ЕРС ємності  ; напруга на котушці
; напруга на котушці  та струм і напруга на конденсаторі
та струм і напруга на конденсаторі 
 .
. і струм в конденсаторі
і струм в конденсаторі  не виникають, а напруга на конденсаторі
не виникають, а напруга на конденсаторі  буде, відповідно до схеми, сталою величиною.
буде, відповідно до схеми, сталою величиною.
 Резистивний опір r. Елемент r, в якому відбувається перетворення електромагнітної енергії в інші види енергії (теплову, променеву, механічну тощо) як необоротний процес, називають активним (резистивним) опором. До кола (рис. 4.8, а) прикладена синусоїдна напруга (для простоти викладення приймемо її початкову фазу
Резистивний опір r. Елемент r, в якому відбувається перетворення електромагнітної енергії в інші види енергії (теплову, променеву, механічну тощо) як необоротний процес, називають активним (резистивним) опором. До кола (рис. 4.8, а) прикладена синусоїдна напруга (для простоти викладення приймемо її початкову фазу 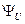 , такою, щодорівнює нулеві):
, такою, щодорівнює нулеві):
 де
де 
 , одержимо закон Ома для кола з резистивним опором для діючих значень напруги і струму:
, одержимо закон Ома для кола з резистивним опором для діючих значень напруги і струму:
 , а коефіцієнт потужності
, а коефіцієнт потужності  .
.
 Цю потужність називають активною потужністю Р.
Цю потужність називають активною потужністю Р.
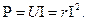

 Котушка індуктивності L. Індуктивний опір XL Обвитки (котушки) електричних машин, трансформаторів, котушки різних електричних пристроїв тощо мають велику індуктивність. Параметрами котушок є резистивний опір r та індуктивність L. Розглянемо спочатку котушку, резистивний опір якої дуже малий і ним можна знехтувати – ідеальну котушку (рис. 4.9, а).
Котушка індуктивності L. Індуктивний опір XL Обвитки (котушки) електричних машин, трансформаторів, котушки різних електричних пристроїв тощо мають велику індуктивність. Параметрами котушок є резистивний опір r та індуктивність L. Розглянемо спочатку котушку, резистивний опір якої дуже малий і ним можна знехтувати – ідеальну котушку (рис. 4.9, а).



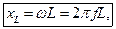
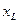 – індуктивний опір котушки,
– індуктивний опір котушки,  =1 Ом.
=1 Ом.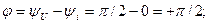
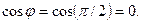


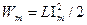 . В інтервалі часу між точками 2 і 3 струм у колі зменшується і енергія магнітного поля котушки повертається в мережу (s (t) < 0). В момент часу, що відповідає точці 3, струм і енергія магнітного поля дорівнюють нулеві.
. В інтервалі часу між точками 2 і 3 струм у колі зменшується і енергія магнітного поля котушки повертається в мережу (s (t) < 0). В момент часу, що відповідає точці 3, струм і енергія магнітного поля дорівнюють нулеві. та опору, що імітує втрати електричної енергії в сталі (
та опору, що імітує втрати електричної енергії в сталі ( Рст) магнітопроводу котушки (
Рст) магнітопроводу котушки ( ,де Е – ЕРС самоіндукції котушки). Повний резистивний опір котушки
,де Е – ЕРС самоіндукції котушки). Повний резистивний опір котушки  , де Рк – активна потужність, що йде на втрати в котушці, Ік – струм котушки. В цьому випадку кут зсуву фаз
, де Рк – активна потужність, що йде на втрати в котушці, Ік – струм котушки. В цьому випадку кут зсуву фаз  < 90°; схема і векторна діаграма мають вигляд, показаний на рис. 4.10.
< 90°; схема і векторна діаграма мають вигляд, показаний на рис. 4.10. . У будь-якій електричній установці ємності утворюються між проводами і землею (в лініях електропересилання) та іншими елементами струмоведучих конструкцій. В силових установках конденсатори використовують для підвищення коефіцієнта потужності; в радіотехніці конденсатори застосовують в коливних контурах, фільтрах тощо.
. У будь-якій електричній установці ємності утворюються між проводами і землею (в лініях електропересилання) та іншими елементами струмоведучих конструкцій. В силових установках конденсатори використовують для підвищення коефіцієнта потужності; в радіотехніці конденсатори застосовують в коливних контурах, фільтрах тощо.




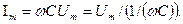


 1 Ом.
1 Ом.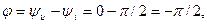 а
а 

 . В наступну чверть періоду між точками 2 і 3 напруга на конденсаторі зменшується і струм змінює напрям; – проходить розряд конденсатора, енергія електричного поля повертається в мережу (s (t) < 0).
. В наступну чверть періоду між точками 2 і 3 напруга на конденсаторі зменшується і струм змінює напрям; – проходить розряд конденсатора, енергія електричного поля повертається в мережу (s (t) < 0). й на втрати, визвані струмом провідності
й на втрати, визвані струмом провідності  в опорі R недосконалого діелектрика. Всі ці втрати виділяються у вигляді тепла. Такого роду конденсатори, які характеризуються втратами, прийнято називати недосконалими конденсаторами. У таких конденсаторах кут зсуву фаз
в опорі R недосконалого діелектрика. Всі ці втрати виділяються у вигляді тепла. Такого роду конденсатори, які характеризуються втратами, прийнято називати недосконалими конденсаторами. У таких конденсаторах кут зсуву фаз  між напругою та струмом за абсолютним значенням менший за
між напругою та струмом за абсолютним значенням менший за  на кут
на кут  , і цей кут називають кутом втрат, який дорівнює:
, і цей кут називають кутом втрат, який дорівнює:

 і
і 
 . На рис. 4.12 наведені ці схеми й відповідні їм векторні діаграми. Значення параметрів цих схем розраховують на основі дослідних даних U, I, та Р, знятих для даного конденсатора. Конденсатори в заступних схемах
. На рис. 4.12 наведені ці схеми й відповідні їм векторні діаграми. Значення параметрів цих схем розраховують на основі дослідних даних U, I, та Р, знятих для даного конденсатора. Конденсатори в заступних схемах  і
і  виступають вже без втрат як ідеальні.
виступають вже без втрат як ідеальні.



 паралельної схеми визначаються так:
паралельної схеми визначаються так:


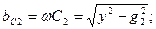

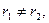
 але
але 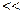
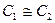 , а співвідношення між ними такі:
, а співвідношення між ними такі:

 В області високих частот
В області високих частот 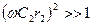 і тоді
і тоді

 залежать від типу діелектрика й можуть змінюватись з частотою, з плином часу, також залежать від температури та напруженості електричного поля.
залежать від типу діелектрика й можуть змінюватись з частотою, з плином часу, також залежать від температури та напруженості електричного поля.
 , a
, a 



 на резистивному опорі збігається за напрямом із вектором струму, вектор
на резистивному опорі збігається за напрямом із вектором струму, вектор 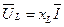 на індуктивності випереджує вектор струму на 90°, вектор напруги на ємності відстає від вектора струму на 90°. Отже, між векторами напруги на індуктивності та ємності утворюється кут, що дорівнює 180°. Вектор напруги, прикладеної до кола, дорівнює геометричній сумі векторів напруг на окремих її ділянках:
на індуктивності випереджує вектор струму на 90°, вектор напруги на ємності відстає від вектора струму на 90°. Отже, між векторами напруги на індуктивності та ємності утворюється кут, що дорівнює 180°. Вектор напруги, прикладеної до кола, дорівнює геометричній сумі векторів напруг на окремих її ділянках: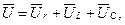












 .
.





 Ом.
Ом. Ом
Ом Ом.
Ом. φ = 51°20',
φ = 51°20', .
.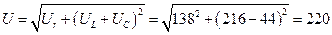 В.
В.


