
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Паралельне з'єднання приймачів у колі змінного струмуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Спочатку розглянемо графоаналітичний метод розрахунку кола з паралельним з'єднанням приймачів. Розглянемо схему з трьох віток. Струм у кожній вітці визначається згідно із законом Ома:
Кут зсуву фаз між струмом кожної вітки і напругою мережі визначається 3 трикутника опорів відповідної вітки через cos φ чи tg φ:
Загальний струм, як випливає із першого закону Кірхгофа, дорівнює геометричній сумі струмів усіх віток:
Значення загального струму визначають графічно із векторної діаграми (рис. 4.15, в), побудову якої починаємо з напруги як із спільної величини для всіх віток схеми. Стрілки кутів φ на векторних діаграмах скеровані від стругу до напруги. Активна потужність кола дорівнює арифметичній сумі потужностей окремих віток:
Реактивна потужність кола дорівнює алгебричній сумі реактивних по тужностей всіх віток, причому реактивну потужність вітки з індуктивністю беруть із знаком "плюс" (кут φ > 0), а вітки з ємністю – зі знаком "мінус" (кут φ<0):
Повна потужність кола Графоаналітичний метод невигідний для розрахунку складніших кіл – громіздкий, вимагає великої точності графічної роботи і не забезпечує високого ступеня точності. Тепер розглянемо аналітичний метод розрахунку розгалужених кіл змінного струму – т.з. класичний метод. В цьому методі використовують провідності, за допомогою яких можна аналітично розрахувати струми всіх віток і напруги на всіх ділянках кола. Струм у кожній вітці кола розкладають на дві складові (рис. 4.15, г), одна з яких – це проекція на вектор напруги
а реактивна складова струму – реактивну потужність:
Із векторної діаграми (рис. 4.15, г) випливає, що:
де
відповідно, активна та реактивна провідності першої вітки. Тут Для другої вітки маємо:
де
Отже
І для k -ї вітки:
Так можна визначити провідності усіх віток схеми и відповідно складові їх струмів Іа та Ір. Загальна активна й реактивна провідності, активна й реактивна складові загального струму схеми дорівнюють сумі відповідних складових:
В цій сумі реактивні провідності віток з індуктивним характером навантаження будуть додатними (зі знаком "плюс"), а віток з ємнісним характером від'ємними (зі знаком "мінус"). Повна еквівалентна провідність і сумарний струм схеми дорівнюють:
Еквівалентний резистивний r Е, реактивний х Еі повний Z Eопори кола (рис. 4.15,б) визначаються за допомогою таких співвідношень:
Тут необхідно відзначити, що якщо bе > 0, то хЕ буде індуктивним опором, а якщо bе < 0, то хЕ – ємнісним, і якщо bе = 0 – тоді хЕ = 0.
Мішане сполучення приймачів Класичний метод розрахунку кіл змінного струму при мішаному сполученні приймачів полягає в тому, що паралельне з'єднання замінюємо еквівалентним послідовним сполученням, а відтак розглядаємо повну схему вже як послідовне з'єднання. Спочатку визначаємо провідності віток, з'єднаних паралельно (рис. 4.16, а):
Потім знаходимо еквівалентні провідності паралельно з'єднаних віток: Далі знаходимо опори r Еі x Eсхеми (рис. 4.16, б):
Рис. 4.16. Мішане сполучення приймачів у колі змінного струму Надалі схему розглядаємо як послідовну і за законом Ома визначаємо струм:
Напруга між точками В і С:
Струми паралельних віток дорівнюватимуть:
Коефіцієнт потужності: Потужності:
Внаслідок того, що індуктивні й ємнісні опори, а також індуктивні й ємнісні провідності можуть взаємно компенсуватись, можливі випадки, коли в колі, яке має реактивні елементи, еквівалентний реактивний опір, і відповідно еквівалентна реактивна провідність дорівнюватимуть нулеві, й тоді струм в такому колі збігається за фазою з напругою, прикладеною до клем цього кола, тобто коло загалом веде себе як активний опір. Явище, при якому струм у колі (рис. 4.18), за наявності у ньому реактивних опорів (індуктивностей та ємностей), збігається за фазою з напругою, прикладеною до цього кола, називають резонансом. При резонансі електричного кола із мережі надходить тільки активна енергія (потужність Р), а реактивна енергія (потужність q) циркулює (коливається) всередині схеми між котушкою індуктивності та конденсатором. 4.8.1. Резонанс у колі з послідовним сполученням елементів r, L, С (резонанс напруг) Повний опір такого кола (рис. 4.19, а) виражається як:
Згідно з визначенням при резонансі виконується умова:
Частоту ω0,
На рис. 4.20 наведені графіки залежностей Ur, Ul, UС, I, r, xС, хL, φ від частоти ƒ для схеми (рис. 4.19) при незмінній напрузі мережі. Якщо Якщо
Якщо В інтервалі частот від ƒ= 0 до ƒрез навантаження має ємнісний характер, струм випереджає за фазою напругу мережі (φ < 0). В інтервалі частот від ƒрез до ƒ = ∞ навантаження має індуктивний характер, струм відстає за фазою від напруги (φ > 0). Найбільше значення напруги на ємності одержується, якщо частота дещо менша за резонансну, а на індуктивності – дещо більша за резонансну. Явище резонансу широко використовують в радіоелектронних пристроях та в заводських промислових установках.
4.8.2. Резонанс у колі з паралельним сполученням елементів r, L, С (резонанс струмів) Спочатку розглянемо паралельне сполучення ідеальних елементів r, L, C (рис. 4.21,а). Із умови резонансу маємо:
З останнього виразу резонансна частота При резонансі струмів загальна провідність схеми у дорівнює активній провідності g, отже, досягає найменшого значення:
На рис. 4.22 наведені графіки залежностей Ir, IL, ІC, І, φ від частоти ƒ для схеми (рис. 4.21, а). Струм в індуктивності зворотно пропорційний частоті IL = U/(2πfL), а струм в конденсаторі прямо пропорційний частоті Іс= U∙2πfC. Струм в колі з активним опором не залежить від частоти Ir=U/r. Значення загального струму, як видно із векторної діаграми, дорівнює Якщо Якщо Якщо Резонанс струмів у колі з реальними елементами (рис. 4.23, a). Із визначення маємо: b = 0, b = bL – bС = 0 чи bL = bc, або з урахуванням (4.40), одержимо:
|
||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1148; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.197.111 (0.01 с.) |

 Як видно із схеми (рис. 4.15, а), для такого кола характерно те, що напруги на кожній вітці схеми однакові й дорівнюють напрузі мережі, а загальний струм дорівнює сумі струмів віток.
Як видно із схеми (рис. 4.15, а), для такого кола характерно те, що напруги на кожній вітці схеми однакові й дорівнюють напрузі мережі, а загальний струм дорівнює сумі струмів віток.





 .
.
 , а кут зсуву фаз між загальним струмом і напругою визначається із векторної діаграми або із співвідношення cos φ = P/S.
, а кут зсуву фаз між загальним струмом і напругою визначається із векторної діаграми або із співвідношення cos φ = P/S. – активна складова
– активна складова  , а друга на лінію, перпендикулярну до напруги – реактивна складова струму
, а друга на лінію, перпендикулярну до напруги – реактивна складова струму  ,
,




 ,
,













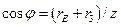 .
. .
. Побудову векторної діаграми для схеми мішаного сполучення бажано починати з напруги на паралельній ділянці, для схеми (рис. 4.16, а) з напруги (рис 4.17). Відтак рисуємо вектори струмів І 1 та І 2 відповідно під кутами φ1 і φ2 до напруги
Побудову векторної діаграми для схеми мішаного сполучення бажано починати з напруги на паралельній ділянці, для схеми (рис. 4.16, а) з напруги (рис 4.17). Відтак рисуємо вектори струмів І 1 та І 2 відповідно під кутами φ1 і φ2 до напруги 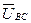 . Знаходимо сумарний струм
. Знаходимо сумарний струм  . Далі рисуємо вектори напруг
. Далі рисуємо вектори напруг  Сума цих напруг дає напругу
Сума цих напруг дає напругу  , прикладену до кола. Послідовність векторів напруг на діаграмі має бути такою самою, що й на схемі.
, прикладену до кола. Послідовність векторів напруг на діаграмі має бути такою самою, що й на схемі.
 4.8. Резонанс в електричних колах
4.8. Резонанс в електричних колах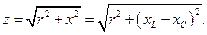
 або
або  чи
чи 

 Як випливає з (4.44), резонансу в колі можна досягти, змінюючи частоту, індуктивність чи ємність. Значення кутової частоти, індуктивності й ємності, за яких настає резонанс, визначаються з (4.44):
Як випливає з (4.44), резонансу в колі можна досягти, змінюючи частоту, індуктивність чи ємність. Значення кутової частоти, індуктивності й ємності, за яких настає резонанс, визначаються з (4.44):
 називають резонансною, вона є власною частотою контуру. З такою частотою в замкненому контурі r – L – С при вимкненні и і закороченні клем а – d схеми (рис. 4.19) енергія вільно коливається між індуктивністю та ємністю.
називають резонансною, вона є власною частотою контуру. З такою частотою в замкненому контурі r – L – С при вимкненні и і закороченні клем а – d схеми (рис. 4.19) енергія вільно коливається між індуктивністю та ємністю.
 Тому, що при резонансі повний опір z досягає найменшого значення z = r, то струм при цьому буде мати має найбільше значення. Оскільки вектори
Тому, що при резонансі повний опір z досягає найменшого значення z = r, то струм при цьому буде мати має найбільше значення. Оскільки вектори  і
і  спрямовані протилежно один до одного й при резонансі однакові за величиною, то вектор прикладеної до кола напруги
спрямовані протилежно один до одного й при резонансі однакові за величиною, то вектор прикладеної до кола напруги  . Може виявитися (при великих xL і хС), що значення напруг UL і UС будуть значно більшими, ніж значення прикладеної напруги U. Отже, при резонансі або в режимах, наближених до резонансу, напруги на котушці та конденсаторі можуть значно перевищувати прикладену до схеми напругу з мережі, що може призвести до аварійних режимів роботи (пошкодження ізоляції, нещасні випадки тощо). Тому при проектуванні й налагодженні електричних схем останні перевіряються на можливість виникнення в них резонансу напруг. Підвищення напруг UL та UС і взаємна їх компенсація при резонансі зумовило назву цього явища – резонанс напруг.
. Може виявитися (при великих xL і хС), що значення напруг UL і UС будуть значно більшими, ніж значення прикладеної напруги U. Отже, при резонансі або в режимах, наближених до резонансу, напруги на котушці та конденсаторі можуть значно перевищувати прикладену до схеми напругу з мережі, що може призвести до аварійних режимів роботи (пошкодження ізоляції, нещасні випадки тощо). Тому при проектуванні й налагодженні електричних схем останні перевіряються на можливість виникнення в них резонансу напруг. Підвищення напруг UL та UС і взаємна їх компенсація при резонансі зумовило назву цього явища – резонанс напруг.
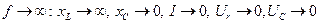 .
.
 опір
опір 
 , струм
, струм 


 .
. або
або  , чи
, чи  визначається так само, як і при резонансі напруг. Досягти умови резонансу можна зміною значень ω, L чи С.
визначається так само, як і при резонансі напруг. Досягти умови резонансу можна зміною значень ω, L чи С. . Загальний струм І = yU = gU теж буде мати найменше значення, а струми
. Загальний струм І = yU = gU теж буде мати найменше значення, а струми  , залежно від значень bL та bC, можуть досягти як завгодно великих значень, що набагато перевищують значення струму в нерозгалуженій частині кола. Збільшення діючих значень струмів у схемі при резонансі в паралельно сполучених вітках зумовило назву – резонанс струмів.
, залежно від значень bL та bC, можуть досягти як завгодно великих значень, що набагато перевищують значення струму в нерозгалуженій частині кола. Збільшення діючих значень струмів у схемі при резонансі в паралельно сполучених вітках зумовило назву – резонанс струмів.


 .
.
 .
. .
.
 За цієї умови (4.47) в схемі (рис. 4.23, а) настає резонанс струмів. На рис. 4.23, б зображена векторна діаграма, що відповідає цьому режиму роботи. Реактивні складові струмів обох віток однакові (
За цієї умови (4.47) в схемі (рис. 4.23, а) настає резонанс струмів. На рис. 4.23, б зображена векторна діаграма, що відповідає цьому режиму роботи. Реактивні складові струмів обох віток однакові ( ), а загальний струм збігається за фазою з напругою.
), а загальний струм збігається за фазою з напругою. Явище резонансу струмів або близьке до цього режиму широко використовується в силових електроенергетичних установках для підвищення коефіцієнта потужності cos φ промислових підприємств.
Явище резонансу струмів або близьке до цього режиму широко використовується в силових електроенергетичних установках для підвищення коефіцієнта потужності cos φ промислових підприємств.


