Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Символічний метод розрахунку електричних кіл синусоїдного струмуСодержание книги
Поиск на нашем сайте
Застосування векторних діаграм (п.п. 4.6-4.7) для розрахунку кіл змінного струму дає змогу досягти наочності та спростити сам розрахунок. Однак векторні діаграми не завжди дають достатню точність і не завжди дають змогу одержати загальний розв'язок задачі. Значним кроком вперед порівняно з векторними діаграмами є введення в теорію змінних струмів Штейнмецом символічного методу, основаного на відображенні векторів комплексними числами. Цей метод дає змогу звести геометричні операції над векторами до алгебричних операцій над комплексними числами.
Деякі положення комплексного числення
Виразивши а і b через модуль (довжину вектора) і кут
де a + jb – алгебрична,
Формула Ейлера показує зв'язок між показниковим та тригонометричним виразами комплексного числа:
і дає змогу переходити від однієї форми запису комплексного числа до іншої. Розглянемо основні геометричні операції над векторами й алгебричні дії над комплексними числами, які їх відображають. 1) Спряжені комплексні числа
Вектор комплексу добутку двох векторів має довжину, що дорівнює добутку модулів, а аргумент а дорівнює алгебричній сумі аргументів множників (рис. 4.24, в). Або в алгебричній формі:
Якщо комплексне число
Ураховуючи оператор повороту
Ділення комплексних чисел
Якщо комплексні числа подані в алгебричній формі, то тоді треба позбутись комплексного числа в знаменнику. Для цього необхідно чисельник і знаменник помножити на спряжене значення знаменника:
Піднесення комплексного числа до степеня
Символічне (комплексне) відображення синусоїдних величин В параграфі (4.2) було розглянуто векторне відображення синусоїдної величини (4.9) з зображенням її вектором на площині х-о-у (рис. 4.26, а). Замінивши декартову систему координат х-о-у комплексною площиною (+1)-0-(+j) (рис. 4.26, б), можемо за аналогією до формули векторного відображення (4.9):
де знак
Зворотний перехід:
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.36.89 (0.008 с.) |


 Як відомо з курсу математики, комплексне число А = а + jb має дві складові: дійсну а та уявну b, які є координатами точки на комплексній площині (рис. 4.24, а). Комплексна площина є прямокутною системою координат, по осі абсцис, яку називають віссю дійсних чисел (+1) – (-1), відкладають дійсну частину комплексного числа а, а по осі ординат – яку називають віссю уявних чисел (+ j) – (– j), відкладають уявну частину комплексного числа b,
Як відомо з курсу математики, комплексне число А = а + jb має дві складові: дійсну а та уявну b, які є координатами точки на комплексній площині (рис. 4.24, а). Комплексна площина є прямокутною системою координат, по осі абсцис, яку називають віссю дійсних чисел (+1) – (-1), відкладають дійсну частину комплексного числа а, а по осі ординат – яку називають віссю уявних чисел (+ j) – (– j), відкладають уявну частину комплексного числа b,  . Комплексне число будемо позначати великою літерою з крапкою зверху. Комплексне число може бути зображене вектором, довжина якого є модулем комплексного числа, а положення визначається кутом (аргументом) а відносно додатного напряму дійсної осі комплексної площини.
. Комплексне число будемо позначати великою літерою з крапкою зверху. Комплексне число може бути зображене вектором, довжина якого є модулем комплексного числа, а положення визначається кутом (аргументом) а відносно додатного напряму дійсної осі комплексної площини.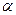 , можна записати комплексне число в тригонометричній формі, а застосувавши формулу Ейлера, комплексне число можна записати в показниковій формі:
, можна записати комплексне число в тригонометричній формі, а застосувавши формулу Ейлера, комплексне число можна записати в показниковій формі:
 – тригонометрична,
– тригонометрична, – показникова форма запису комплексного числа;
– показникова форма запису комплексного числа;

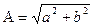 – модуль комплексного числа;
– модуль комплексного числа; – аргумент комплексного числа;
– аргумент комплексного числа; 
 і
і  мають однакові модулі й однакові, але протилежні за знаком аргументи. Спряжені комплексні числа є дзеркальним відображенням один одного відносно осі дійсних чисел (рис. 4.25, а).
мають однакові модулі й однакові, але протилежні за знаком аргументи. Спряжені комплексні числа є дзеркальним відображенням один одного відносно осі дійсних чисел (рис. 4.25, а). 2) Додавання чи віднімання двох (або більше) комплексних чисел можна провести аналітично:
2) Додавання чи віднімання двох (або більше) комплексних чисел можна провести аналітично: або графічно за правилом складання векторів (рис. 4.24, б).
або графічно за правилом складання векторів (рис. 4.24, б). 3) Добуток двох комплексних чисел, які відображають два вектори
3) Добуток двох комплексних чисел, які відображають два вектори 
 єкомплексне число, якому відповідає вектор
єкомплексне число, якому відповідає вектор  :
: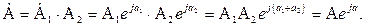

 , то нове комплексне число
, то нове комплексне число 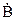 буде мати цей самий модуль А, але повернутий на кут
буде мати цей самий модуль А, але повернутий на кут 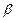 проти стрілки годинника, якщо
проти стрілки годинника, якщо 
 , згідно з рис. 4.25, б або за формулою Ейлера, можна підрахувати
, згідно з рис. 4.25, б або за формулою Ейлера, можна підрахувати  :
: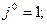



 і т.д.
і т.д. де
де 
 .
.


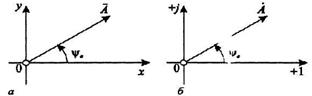

 записати формулу символічного (комплексного) відображення синусоїдної величини, яка буде мати такий вигляд:
записати формулу символічного (комплексного) відображення синусоїдної величини, яка буде мати такий вигляд:
 чи
чи  означає "відповідає", "відображає", а
означає "відповідає", "відображає", а 
 Приклад 4.3. Розглянемо декілька прикладів переходу від миттєвого значення синусоїдної величини до комплексного її відображення, і навпаки.
Приклад 4.3. Розглянемо декілька прикладів переходу від миттєвого значення синусоїдної величини до комплексного її відображення, і навпаки.