
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні фізичні величини магнітного поляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
3.1.1. Магнітна індукція (В) Магнітні поля, подібно до електричних, є засобом описання взаємодії заряджених частин. Електричне поле визначається силовою дією на нерухомі заряди. Магнітне поле визначається силою, що діє на рухомі заряди, ця сила пропорційна швидкості руху заряду і залежить від його напряму. Експериментально встановлена формула визначення цієї сили магнітного поля:
де
Величина B із (3.1) визначається як
Якщо α = 0; q =+1; V = 1, тоді Одиницею вимірювання магнітної індукції всистемі СІ є тесла:
Магнітний потік (Ф) Величиною, яка служить для інтегральної оцінки магнітного поля, є магнітний потік (Ф) – потік вектора магнітної індукції крізь деяку поверхню. Визначимо магнітний потік крізь поверхню S, обнесену контуром l (рис. 3.2). Наочно магнітний потік зображають як сукупність магнітних ліній крізь поверхню S. Звичайно під час обчислення магнітного потоку крізь довільну поверхню в неоднорідному магнітному полі поверхню поділяють на нескінченно малі поверхні dS. В межах кожної з елементарних площинок dS магнітну індукцію вже можна вважати однаковою. Тоді елементарний потік dΦ крізь поверхню dS дорівнює:
а крізь всю поверхню S:
Одиницею вимірювання магнітного потоку є 1 вебер (1 Вб = 1 В∙с):
Принцип неперервності магнітного потоку (магнітних ліній) математично формулюється так:
тобто магнітний потік крізь будь-яку замкнену поверхню дорівнює нулеві, 3.1.3. Намагніченість речовин (J). Напруженість магнітного поля (H). Магнітна проникність (μ)
Магнітне поле колового струму характеризується магнітним моментом, напрям якого визначається за правилом правого гвинта.
Намагніченість речовини можна пояснити, враховуючи поняття магнітного моменту
де Виділимо всередині намагніченої речовини елементарний об'єм ∆V і для цього об'єму геометрично складемо всі
Отже, намагніченість речовини дорівнює геометричній сумі магнітних моментів елементарних струмів, віднесеної до одиниці об'єму речовини. Намагніченість вимірюється: [ J ] = 1 А/м. Розглянуті вище величини магнітного поля – магнітна індукція, магнітний потік і намагніченість речовини ( За відсутності намагніченості середовища (J = 0 – для вакууму) співвідношення між В та Η встановлюється залежністю:
де μ0 – магнітна стала або магнітна проникність вакууму (μ0= 4π·10-7 Гн/м = 125-10-8 Гн/м), теж характеризує магнітні властивості повітря, оскільки для повітря μпов=4,000012·π·10-7 Γн/м Для будь-якої речовини, внесеної у зовнішнє магнітне поле напруженістю (
де k =
Величина (1 + k) у виразі (3.9) є відносною магнітною проникністю:
Тоді
де Якщо власні магнітні моменти атомів деяких речовин дорівнюють нулеві, то при внесенні такої речовини в зовнішнє магнітне поле, утворене, наприклад, в повітряному середовищі, наведені індуковані моменти, напрямлені проти поля (тобто Залежність J = f (H)для діамагнетиків і парамагнетиків лінійна (прямі лінії 1 і 2 на рис. 3.5) і досить незначна, тому що коефіцієнт магнітної сприйнятності достатньо малий (k = 10-4 – 10-6). Крім цього, характерною особливістю цих речовин є зменшення або постійність k і μ при зростанні температури й відсутність, як правило, магнітного гістерезису.
У квантовій механіці доведено, що природа феромагнетизму визначається в основному спіновими магнітними моментами електронів, тому що орбітальні магнітні моменти електронів є послабленими за рахунок поля сусідніх атомів. Спінові моменти додаються один з одним, викликають самовільну (спонтанну) намагніченість речовини навіть за відсутності зовнішнього поля. Ця намагніченість є найхарактернішою ознакою феромагнетизму. У електротехнічних розрахунках електричних машин, трансформаторів, апаратів, приладів тощо відносна магнітна проникність діамагнітних та парамагнітних матеріалів приймається такою, що дорівнює одиниці (μ = 1). Для феромагнітних матеріалів відносна магнітна проникність може досягти тисяч і десятків тисяч одиниць (103... 104) і залежить від величини магнітної індукції. Закон повного струму Цей закон дає змогу за даними значеннями струмів, що створюють магнітне поле, й координат точки визначити напруженість магнітного поля в цій точці, незалежно від середовища, в якому проходять струми чи розташована ця точка. Формулюється він так: лінійний інтеграл вектора напруженості магнітного поля вздовж замкненого контуру дорівнює електричному струмові, що охоплюється цим контуром, тобто струмові, який проходить крізь поверхню, що обмежується цим контуром:
Додатний напрям контуру пов'язаний з напрямом електричного струму правилом правого гвинта. В правій частині (3.13) під величиною і слід розуміти струм провідності, струм перенесення, а також струми зміщення, які проходять крізь поверхню, обмежену контуром інтегрування (l). Сума цих струмів (провідності, переносу й зміщення) може бути названа повним струмом, тому рівність (3.13) називають законом повного струму. Для ілюстрації запишемо закон повного струму для контуру, що охоплює площину S (рис. 3.6):
Запишемо закон повного струму ще для контуру l (рис. 3.6):
Магніторушійна сила та магнітна напруга. Під магніторушійною силою (МРС), або намагнічувальною силою розуміють праву частину рівності(3.13) – величину ∑ i і позначають її літерою F. Магніторушійна сила котушки з кількістю витків w, по якій протікає струм і, дорівнює F = wi та скерована відносно струму за правилом правого гвинта. Під магнітною напругою ділянки контуру l (UM ab)будемо розуміти величину:
Якщо поле рівномірне й вектори Одиниці вимірювання магніторушійної сили й магнітної напруги однакові й тотожні з одиницею вимірювання сили струму, тобто [ U m] = [F] = 1 А. Інколи одиницю вимірювання МРС називають ампервитком і позначають її символом Ав.
Феромагнітні матеріали
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1132; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.237.52 (0.008 с.) |

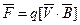
 або в скалярних величинах
або в скалярних величинах ,
,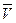 – вектор швидкості рухомого заряду;
– вектор швидкості рухомого заряду;  – вектор магнітної індукції; α – кут між вектором
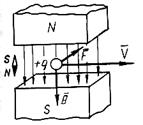
– вектор магнітної індукції; α – кут між вектором  Пояснимо сказане. Нехай додатний заряд (+q)рухається в магнітному полі із швидкістю (
Пояснимо сказане. Нехай додатний заряд (+q)рухається в магнітному полі із швидкістю ( ), напрям якої можна визначити за правилом лівої руки, а значення із (3.1).
), напрям якої можна визначити за правилом лівої руки, а значення із (3.1). , або
, або 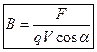
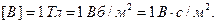




 (3.3)
(3.3) Якщо вектор магнітної індукції перпендикулярний до площини S і в усіх її точках і має однакове значення, співвідношення (3.3) набере такого вигляду:
Якщо вектор магнітної індукції перпендикулярний до площини S і в усіх її точках і має однакове значення, співвідношення (3.3) набере такого вигляду: , або
, або  .
.
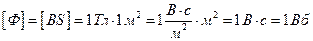 .
.
 Всередині будь-якої речовини існують елементарні струми й при відсутності зовнішніх електромагнітних полів. Ми уявляємо собі ці струми як рух електронів по орбітах всередині атомів речовини й як обертання електронів навколо своїх осей.
Всередині будь-якої речовини існують елементарні струми й при відсутності зовнішніх електромагнітних полів. Ми уявляємо собі ці струми як рух електронів по орбітах всередині атомів речовини й як обертання електронів навколо своїх осей. Електрони володіють орбітальним і спіновим магнітними моментами, якіможуть бути спрямовані або в один, або в різні боки (рис. 3.3).
Електрони володіють орбітальним і спіновим магнітними моментами, якіможуть бути спрямовані або в один, або в різні боки (рис. 3.3).
 Сумарний магнітний момент одиниці об'єму речовини (з врахуванням власних і наведених моментів) називають намагніченістю J. Поняття намагніченості не має змісту для окремого атома, а стосується лише групи атомів і характеризує стан речовини, який вона набуває в результаті намагнічування. В міжнародній системі одиниць (СІ) намагніченість – це внутрішнє магнітне поле речовини, зумовлене магнітними моментами його атомів.
Сумарний магнітний момент одиниці об'єму речовини (з врахуванням власних і наведених моментів) називають намагніченістю J. Поняття намагніченості не має змісту для окремого атома, а стосується лише групи атомів і характеризує стан речовини, який вона набуває в результаті намагнічування. В міжнародній системі одиниць (СІ) намагніченість – це внутрішнє магнітне поле речовини, зумовлене магнітними моментами його атомів. елементарного струму i 0 (рис. 3.4). Магнітним моментом елементарного струму називають добуток величини i 0 на площину S 0, що охоплюється цим струмом. Магнітний момент – векторна величина, напрям його приймають вздовж перпендикуляра
елементарного струму i 0 (рис. 3.4). Магнітним моментом елементарного струму називають добуток величини i 0 на площину S 0, що охоплюється цим струмом. Магнітний момент – векторна величина, напрям його приймають вздовж перпендикуляра  до площини S 0і зорієнтованого зі струмом за правилом правого гвинта. Отже,
до площини S 0і зорієнтованого зі струмом за правилом правого гвинта. Отже,
 – вектор, що кількісно дорівнює S0 і скерований по
– вектор, що кількісно дорівнює S0 і скерований по  – сумарний магнітний момент об'єму ∆V:
– сумарний магнітний момент об'єму ∆V:  . Поділивши величину
. Поділивши величину  в даній точці поля, треба взяти границю відношення
в даній точці поля, треба взяти границю відношення 
 ). Ця величина не залежить від середовища, в якому розглядається магнітне поле, а залежить тільки від величини струму, що створив це поле, та координат точки, в якій визначається
). Ця величина не залежить від середовища, в якому розглядається магнітне поле, а залежить тільки від величини струму, що створив це поле, та координат точки, в якій визначається 
 μ0.
μ0.


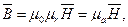
 – абсолютна магнітна проникність даного середовища. Для вакууму (теж для повітря) μ a = μ0, а значить, k = 0.
– абсолютна магнітна проникність даного середовища. Для вакууму (теж для повітря) μ a = μ0, а значить, k = 0.
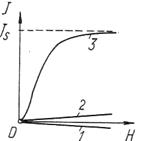 Другу групу речовин, для яких відносна магнітна проникність набагато більша від одиниці (μ» 1, μ а» μ0), називають феромагнетиками (сильно магнітними). До них належать: залізо, нікель, кобальт, гадоліній, диспрозій та сплави цих елементів. Вони мають подібні магнітні властивості. Відносна магнітна проникність може досягати десятків і сотень тисяч одиниць та значною мірою залежить від напруженості поля і температури. Намагніченість J навіть при дуже малих магнітних полях буває набагато більшою від напруженості Η і швидко досягає насичення Js, а залежність J = f (H)перестає бути лінійною (крива 3 на рис. 3.5). Зі збільшенням температури намагнічуючого взірця значення Js зменшується, тому що збільшується тепловий рух і послаблює орієнтацію власних магнітних моментів. При нагріванні вище від деякої критичної для певної речовини температури (її називають точкою Кюрі) речовина втрачає феромагнітні властивості (перетворюється в парамагнетик). Одночасно змінюються її фізичні характеристики: теплоємність, j електропровідність тощо.
Другу групу речовин, для яких відносна магнітна проникність набагато більша від одиниці (μ» 1, μ а» μ0), називають феромагнетиками (сильно магнітними). До них належать: залізо, нікель, кобальт, гадоліній, диспрозій та сплави цих елементів. Вони мають подібні магнітні властивості. Відносна магнітна проникність може досягати десятків і сотень тисяч одиниць та значною мірою залежить від напруженості поля і температури. Намагніченість J навіть при дуже малих магнітних полях буває набагато більшою від напруженості Η і швидко досягає насичення Js, а залежність J = f (H)перестає бути лінійною (крива 3 на рис. 3.5). Зі збільшенням температури намагнічуючого взірця значення Js зменшується, тому що збільшується тепловий рух і послаблює орієнтацію власних магнітних моментів. При нагріванні вище від деякої критичної для певної речовини температури (її називають точкою Кюрі) речовина втрачає феромагнітні властивості (перетворюється в парамагнетик). Одночасно змінюються її фізичні характеристики: теплоємність, j електропровідність тощо.

 Напрям обходу контуру показаний пунктирною лінією. Струми і 0та і kв праву частину наведеної рівності не увійшли тому, що вони не охоплюються контуром l.
Напрям обходу контуру показаний пунктирною лінією. Струми і 0та і kв праву частину наведеної рівності не увійшли тому, що вони не охоплюються контуром l.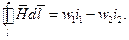
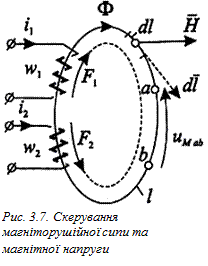 Тут струм і1 охоплює контур l w1 разів, а струм і2 – w2 разів. При обході контуру за годинниковою стрілкою струм і1 та напрям обходу скеровані за правилом правого гвинта, а струм і2 – за лівим гвинтом.
Тут струм і1 охоплює контур l w1 разів, а струм і2 – w2 разів. При обході контуру за годинниковою стрілкою струм і1 та напрям обходу скеровані за правилом правого гвинта, а струм і2 – за лівим гвинтом.
 і
і  збігаються, тоді Um= Нl. Як i в електричних колах, напрям магнітної напруги будемо позначати однією стрілкою, скерованою до точки (а) вищого магнітного потенціалу, ураховуючи, що у контурі l магнітний потік скерований від точки а до b.
збігаються, тоді Um= Нl. Як i в електричних колах, напрям магнітної напруги будемо позначати однією стрілкою, скерованою до точки (а) вищого магнітного потенціалу, ураховуючи, що у контурі l магнітний потік скерований від точки а до b.


