
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення індукції магнітного поля за допомогою терезів АмпераСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ЗМІСТ
Вступ............................................................................................................................... 4
Лабораторна робота № 45 Визначення індукції магнітного поля
Лабораторна робота № 46 Визначення горизонтальної складової напруженості
Лабораторна робота №47. Визначення питомого заряду електрона....................................................... 20
Лабораторна робота №49 Визначення точки Кюрі феромагнетиків..................................................... 29
Лабораторна робота № 50 Зняття петлі гістерезису феромагнетика
Лабораторна робота № 53 Вивчення роботи релаксаційного генератора............................................ 47
Лабораторна робота № 54 Визначення індуктивності соленоїда та ємності конденсатора
Лабораторна робота № 55 Вивчення резонансу в електричному коливальному контурі............. 68
Лабораторна робота № 60 Визначення довжини електромагнітної хвилі
Перелік використаних джерел.............................................................................. 87
ВСТУП Даний практикум узагальнює багаторічний досвід методики проведення лабораторних робіт з розділу „Електрика і магнетизм” з курсу „Фізика” в Івано-Франківському національному технічному університеті нафти і газу. Розділ „Електрика і магнетизм” без перебільшення можна назвати одним із найважливіших розділів курсу фізики для підготовки майбутніх інженерів всіх спеціальностей. Фізика – експериментальна наука, тому даний лабораторний практикум націлює студентів на те, щоб вони самі стали для себе першовідкривачами тих чи інших фізичних законів. Тому в практикумі значне місце відводиться принципу, ідеї фізичного експерименту. Студент повинен добре розуміти, навіщо досліджується дане фізичне явище, як його дослідити, як оформити результати проведених дослідів, та як оцінити похибки експерименту. Даний лабораторний практикум може бути корисним і тим, що він в багатьох випадках націлює студентів ІФНТУНГ на практичне застосування відповідних явищ та законів електрики і магнетизму.
Лабораторна робота № 45 Лабораторна робота №49 ВИЗНАЧЕННЯ ТОЧКИ КЮРІ ФЕРОМАГНЕТИКІВ МЕТА РОБОТИ:ознайомитись з основними властивостями феромагнетиків та освоїти методику експериментального визначення точки Кюрі. ПРИЛАДИ:досліджуваний феромагнетик, нагрівач, джерело змінного струму, термопара, мікровольтметр.
ТЕОРЕТИЧНІ ВІДОМОСТІ Питання магнітних властивостей речовин мають велике практичне значення. Так, в останній час широкого застосування набули штучні напівпровідники магнітні матеріали – ферити. Феритні матеріали застосовують в магнітних стрічках та дисках для магнітного запису інформації. Феритні осердя використовують у високочастотній техніці. Разом з тим, феромагнітні матеріали можуть втратити свої особливі магнітні властивості при температурі, яка називається точкою Кюрі (в честь французького фізика П. Кюрі, який вивчав це явище). Тому визначення точки Кюрі набуває значного практичного значення. Щоб зрозуміти питання, пов'язані з точкою Кюрі та з методикою її визначення доцільно розглянути короткий виклад теорії феромагнетизму.
ПРИРОДА ФЕРОМАГНЕТИЗМУ
Особливі властивості феромагнетиків зумовлені наявністю в них областей спонтанного (самовільного) намагнічення, які отримали назву доменів (від французького - володіння). Домени мають розміри порядку 10-2 – 10-3 мм, в яких величезна кількість спінових магнітних моментів електронів строго орієнтованими в одному напрямі і причиною цього є квантові ефекти. В спонтанній орієнтації спінових моментів електронів основну роль відіграють особливі взаємодії, які в квантовій механіці називається обмінними. Обмінна взаємодія приводить до того, що в феромагнетиках енергетично вигідним є стан, при якому спіни електронів в незаповнених оболонках сусідніх атомів є паралельними в зв'язку з чим і виникає спонтанне намагнічення. Напрям спонтанного намагнічення визначається внутрішньою будовою феромагнетика. Наприклад, чисте залізо має внутрішню будову з об’ємноцентрових кубічних кристалічних решіток (рис. 49.2). Встановлено, що в такому залізі вісями найбільш легкого намагнічення є вісі куба. Це значить, що спінові магнітні моменти електронів можуть орієнтуватись в одному з шести напрямів: ±X; ±Y; ±Z, ці напрямки мають “перевагу” над іншими можливими напрямами в кристалі заліза.
Відомо, що будь-яка система намагається зайняти стан з мінімальною енергією. Тому, якщо даний феромагнетик буде являти собою сукупність двох доменів з протилежними напрямами намагнічення (рис. 49.3б), то зовнішнє магнітне поле буде меншим, відповідно такий стан феромагнетика буде більш енергетично вигідним, ніж попередній. На (рис. 49.3в) вказаний такий випадок, коли взагалі зовнішнє магнітне поле відсутнє. Тут феромагнетик “розбився” на такі окремі домени, де їх магнітні поля замикаються і даний стан феромагнетика стає найбільш енергетично вигідним. Існування доменів в феромагнетиках експериментально доведено різними дослідами. Наприклад, один з методів полягає в утворенні порошкових структур. Так, якщо на відполіровану поверхню феромагнетика нанести шар рідини, в якій знаходиться надзвичайно дрібні крупинки феромагнітного порошку Fe2O3, то ці крупинки, притягуючись доменами, “вирисовують” їх границі. Так порошкові фігури можна спостерігати в мікроскоп навіть при невеликому збільшенні (в сто разів).
4. ТОЧКА КЮРІ ДЛЯ ФЕРОМАГНЕТИКІВ. Для кожного феромагнетика існує певна температура при якій відбувається руйнування його доменів, феромагнетик перетворюється в парамагнетик. Ця температура, як вже вище вказувалось, називається точкою Кюрі. При охолодженні феромагнетика нижче точки Кюрі в феромагнетику виникають магнітні домени. Перехід від феромагнітних властивостей до парамагнітних є прикладом фазового переходу другого роду[6]. Прикладом фазового переходу другого роду може бути перехід металу в надпровідний стан. До фазового переходу другого роду відноситься надтекучість гелію, коли повністю зникає внутрішнє тертя. Нагадаємо, що фазові переходи першого роду (плавлення, випаровування) супроводжуються стрибкоподібною зміною внутрішньої енергії тіла і пов’язані з поглинанням теплоти (теплота плавлення, теплота випаровування). Для того, щоб зруйнувати домен, не потрібно додаткової енергії, достатньо нагрівання феромагнетика, його внутрішня енергія буде збільшуватись і при температурі Кюрі без додаткових затрат енергії відбувається руйнування доменів.
Таблиця 49.1
3. За отриманими даними побудувати залежність сили струму у вторинній обмотці трансформатора від показів мікровольтмера термопари (верхня частина графіка, рис. 49.6). В нижню частину графіка перенести градуйовочну пряму термопари, яка вказана на лабораторному стенді. 4. Для визначення точки Кюрі з точки перегину експериментальної кривої проводять вертикальну лінію до перетину з градуйовочною прямою термопари. Ордината точки перетину дає значення точки Кюрі – температуру t к. 5. Точка Кюрі визначається похибкою графічного методу. Положення точки перегину не є точним, а знаходиться в межах ±DX по вісі абсцис. Тоді продовживши координати можливого відхилення до перетину з градуйовочною прямою, визначають похибку температури t, як це вказано на (рис. 49.6). Значення можливого відхилення ±DX від точки перегину визначає та обґрунтовує сам експериментатор. КОНТРОЛЬНІ ПИТАННЯ 1. В чому полягала гіпотеза Ампера про природу магнетизму? 2. Дайте означення магнітного моменту контуру зі струмом. За яким правилом визначається напрям вектора магнітного моменту? 3. Дайте означення намагніченності (вектора намагнічення) речовини. 4. Дайте означення магнітної сприйнятливості та магнітної проникності речовини. Який між ними існує зв’язок? 5. Приведіть класифікацію речовин на діамагнетики, парамагнетики і феромагнетики (в залежності від їх магнітної сприйнятливості та магнітної проникності). 6. Яка природа феромагнетизму? Чому феромагнетик “розбивається” на окремі домени? Як експериментально довести існування доменів? 7. Дайте означення точки Кюрі для феромагнетиків. Яка різниця між фазовими переходами першого і другого роду? 8. В чому полягає методика експериментального визначення точки Кюрі для феромагнетиків? 9. Навести схему лабораторної установки для визначення точки Кюрі для феромагнетиків. 10. Яка послідовність виконання роботи? Лабораторна робота № 50 ЗНЯТТЯ ПЕТЛІ ГІСТЕРЕЗИСУ ФЕРОМАГНЕТИКА
МЕТА РОБОТИ: ознайомитися з основними властивостями феромагнетиків та освоїти методику експериментального визначення цих характеристик методом зняття петлі гізтерезису. ПРИЛАДИ: досліджуваний феромагнетик з обмотками, джерело змінного струму, ЛАТР, електронний осцилограф.
1. МАГНІТНІ МОМЕНТИ ЕЛЕКТРОНІВ. НАМАГНІЧЕНІСТЬ РЕЧОВИНИ (ВЕКТОР НАМАГНІЧЕННЯ) Всі речовини є магнетиками, тобто намагнічуються. Інша справа, яке це намагнічення, як його характеризувати. Відповідь на такі питання можна отримати, вивчаючи внутрішню будову речовини, розглядаючи ті структурні елементи, які визначають магнітні властивості даної речовини. Так, електрон, який обертається навколо ядра атома еквівалентний коловому струму
Крім орбітального магнітного моменту електрон володіє ще власним магнітним моментом, який отримав назву спінового магнітного моменту. Магнітним моментом володіють і ядра атомів, але їх вклад в магнітні властивості речовини дуже малий і тому магнітні властивості речовини визначаються орбітальними та спіновими магнітними моментами, які входять в склад атомів (молекул) речовини. Якщо ці магнітні моменти орієнтовані хаотично, то речовина не намагнічена і векторна сума магнітних моментів електронів дорівнює нулю. В зовнішньому магнітному полі відбувається орієнтація магнітних моментів електронів і їх векторна сума вже не дорівнює нулю (речовина намагнічується). Відношення (50.2) сумарного магнітного моменту атомів речовини до об’єму речовини V кількісно характеризує її намагнічення і називається намагніченістю або вектором намагнічення.
2. МАГНІТНА СПРИЙНЯТЛИВІСТЬ І МАГНІТНА ПРОНИКНІСТЬ РЕЧОВИНИ. ДІАМАГНЕТИКИ, ПАРАМАГНЕТИКИ ТА ФЕРОМАГНЕТИКИ У несильних магнітних полях намагніченість речовини пропорційна напруженості Н зовнішнього магнітного поля (50.3), де c -("хі") - магнітна сприйнятливість речовини, безрозмірна величина, яка характеризує магнітні властивості даної речовини (як ця речовина "сприймає" магнітне поле). Якщо ж порівняти індукцію В магнітного поля[7] в речовині з індукцією В 0 магнітного поля у вакуумі (намагнічуючого поля), то отримаємо іншу характеристику магнітних властивостей речовини - магнітну проникність m (50.4.). Зв'язок між магнітною проникністю m та магнітною сприйнятливістю c встановлюється співвідношенням (50.5).
У залежності від значень c або m речовини за своїми магнітними властивостями можна поділити на три основні групи. а) Діамагнетики, для яких магнітна сприйнятливість від'ємна і дуже мала за абсолютним значенням. Наприклад, для води c=-0,000009. Згідно (50.5) для діамагнетиків m<1. б) Парамагнетики, в яких магнітна сприйнятливість мала, але додатня. Так, для алюмінію c =1,000023. Магнітна проникність парамагнетиків m >1. в) Феромагнетики, які характеризуються великим додатнім значенням c і m знаходиться в межах (103-105). До феромагнетиків відносяться залізо, нікель, кобальт, гадоліній а також окремі сплави. В останній час широкого застосування набули напівпровідникові феромагнітні матеріали - ферити.
3. ПРИРОДА ФЕРОМАГНЕТИЗМУ. НАМАГНІЧЕНІСТЬ ФЕРОМАГНЕТИКІВ. КРИВА НАМАГНІЧЕННЯ Особливі магнітні властивості феромагнетиків пояснюються на основі їх доменної структури (домен - від французького слова "володіння").
Дія магнітного поля на домени на різних стадіях намагнічення є різна.
На даній кривій ділянка 1 відповідає збільшенню намагнічення за рахунок росту доменів та їх орієнтації вздовж поля, а ділянка 2 характеризує насичення[8].
4. МАГНІТНИЙ ГІСТЕРЕЗИС. ПЕТЛЯ ГІСТЕРЕЗИСУ Для феромагнетиків крива намагнічення і розмагнічення не співпадають. Таке явище називається магнітним гістерезисом[9] (від гр. слова - "відставати").
На отриманій залежності В від Н, яка називається петлею гістерезису (рис. 50.4) можна виділити такі основні ділянки: 0-1 - намагнічення феромагнетика; 1-2 - зовнішнє магнітне поле зменшується до нуля, але в феромагнетику спостерігається залишкова намагніченість, залишається поле індукцією В 3; 2-3 - намагніченість раніше намагніченого феромагнетика зникає під дією поля напруженістю Н к, яка має напрям протилежний полю, що викликав дане намагнічення. Така напруженість називається коерцитивною силою (від гр. слова - "стримувати"). Далі феромагнетик знову намагнічується до насичення (3-4), потім зовнішнє магнітне поле зменшується (4-5) і знову маємо залишкову намагніченість В 3, тільки в протилежному напрямі. Ділянка 5-6 відповідає розмагніченню, а 6-1 намагніченню до насичення до початкового значення.
Тому, визначивши в різних точках ділянки 0-1 (рис.50.4) індукцію В та напруженість поля Н, за формулою (50.7) можна підрахувати ряд значень магнітної проникності:
B=m0mН (50.6)
На основі цих значень будують графік залежності магнітної проникності m досліджуваного феромагнетика від напруженості Н намагнічуючого поля (рис. 50.5). Такий графік має точку перегину, яка визначає максимальне значення магнітної проникності. Величини В 3, Н к та m max є основними характеристиками феромагнетиками, які досліджують в даній роботі.
5. МЕТОДИКА ЕКСПЕРИМЕНТАЛЬНОГО МЕТОДУ ЗНЯТТЯ ПЕТЛІ ГІСТЕРЕЗИСУ ЗА ДОПОМОГОЮ ОСЦИЛОГРАФА
На рис. 50.6 наведена принципова схема лабораторної установки для зняття петлі гістерезису за допомогою електронного осцилографа. Досліджуваний феромагнетик являє собою тороїд (кільце) з двома обмотками: І - первинна; ІІ - вторинна.
Згідно закону Ома при силі струму І напруга U x на кінцях резистора R рівна (50.9) і тоді, як випливає з (50.8), ця напруга буде пропорційна напруженості Н намагнічуючого поля (50.10). Це змінне магнітне поле (струм змінний) індукує у вторинній обмотці тороїда електрорушійну силу ЕРС, яка згідно закону електромагнітної індукції пропорційна швидкості зміни магнітного потоку (50.11). Магнітний потік через витки вторинної обмотки дорівнює (50.12), де N 2 - число витків обмотки; S - площа поперечного перерізу обмотки (тут це площа поперечного перерізу тороїда, на який намотана обмотка); В - індукція магнітного поля.
З (50.11) і (50.12) отримаємо рівняння (50.13), де значення індукції В магнітного поля входить під знак диференціала. Для того, щоб отримати електричний сигнал, який пропорційний індукції, використовують електричну схему з резистора R 2 та конденсатора С (рис.50.6). Така електрична схема називається інтегруючим ланцюжком, де аналогом математичного інтегрування розв'язку рівняння (50.13) є накопичення (сумування) заряду на обкладинках конденсатора. На вхід такого ланцюжка подається диференціальна величина Для того, щоб отримати петлю гістерезису, використовують електричний осцилограф. На одну пару пластин (відхилення по горизонталі - вхід «Х») подають напругу U x, яка пропорційна напруженості Н намагнічуючого поля. На другу пару пластин (відхилення по вертикалі - вхід «Y») подають напругу U y, яка пропорційна індукції В магнітного поля в досліджуваному феромагнетику. Електронний промінь, здійснюючи такі зміщення у взаємно перпендикулярних напрямах, опише на екрані залежність В від Н. За один період змінного струму електронний промінь опише повну петлю гістерезису, а за кожний наступний повторить її. Тобто на екрані осцилографа буде видна нерухома петля гістерезису даного феромагнетика. Координати точок отриманої петлі визначають за міліметровими поділками шкали на екрані осцилографа. При розрахунках магнітних властивостей феромагнетика необхідно від поділок шкали в міліметрах перейти до відповідних магнітних величин (В та Н). Для цього зручно скористуватись чутливістю осцилографа. Для горизонтально відхиляючих - (50.16), де Х - зміщення променя по горизонталі; Y - по вертикалі при відповідних напругах U x і U y. Вимірявши в міліметрах на екрані осцилографа координати X і Y точок петлі гістерезису, з (50.15) і (50.16) та (50.10) і (50.14) отримаємо відповідні значення напруженості Н (50.17) намагнічуючого поля та індукції В (50.18) поля в феромагнетику.
6. ПОСЛІДОВНІСТЬ ВИКОНАННЯ РОБОТИ
Перед початком виконання роботи ознайомтесь з усіма приладами. Особливу увагу зверніть на ручки керування осцилографом: яскравість, фокус, ручки зміщення променя по горизонталі і вертикалі, ручки підсилення по вертикалі і горизонталі. 1. Згідно рис 50.6 зібрати електричну схему, при цьому джерела струму повинні бути вимкнутими (вимкнутий осцилограф і ЛАТР). 2. В табл. 50.1 занести значення величин, які вказані на стенді:
Таблиця 50.1.
3. Ввімкнути осцилограф. Встановити електронний промінь в центр координатної сітки (користуватись ручками: зміщення променя по горизонталі і вертикалі). 4. Ввімкнути ЛАТР і, збільшуючи вихідну напругу, отримати на екрані зображення максимальної петлі гістерезису (з ділянками насичення). Ручками підсилення по вертикалі і горизонталі домогтись того, щоб петля займала більшу частину екрана. 5. Перенести зображення отриманої петлі гістерезису на міліметровий папір (рис. 50.7) і на рисунку записати значення чутливостей осцилографа: Ky і Kx. Відлік значень Ky та Kx провести по відповідним шкалам біля ручок: “підсилення по вертикалі”; “підсилення по горизонталі”.
7. РОЗРАХУНОК ЗАЛИШКОВОГО НАМАГНІЧЕННЯ ТА КОЕРЦИТИВНОЇ СИЛИ ДОСЛІДЖУВАНОГО ФЕРОМАГНЕТИКА
2. Виміряти віддаль b=2у між точками петлі, які визначають залишкову намагніченість В 3. У формулу (50.18) підставити 3. Похибки D H k і D B 3 вираховують за формулами похибок (50.19) і (50.20), які виводять з робочих формул. (50.17) та (50.18) (похибками числа витків можна нехтувати).
Похибки D К х і D К у рівні половині ціни найменшої поділки відповідних шкал чутливості осцилографа. Похибка D х і D у оцінює сам експериментатор.
8. ДОДАТКОВЕ ЗАВДАННЯ: ВИЗНАЧЕННЯ МАГНІТНОЇ ПРОНИКНОСТІ ДОСЛІДЖУВАНОГО ФЕРОМАГНЕТИКА Після того, як на екрані осцилографа отримана максимальна петля гістерезису, послідовно зменшуючи напругу на первинній обмотці тороїда, отримують ряд часткових петель, поки петлі не стягнуться в точку. Для кожної петлі гістерезису на міліметровому папері відмічають положення (координати) вершин петлі. За формулами (50.17) і (50.18) розраховують значення напруженості та індукції магнітного поля у відповідних вершинах часткових петель гістерезису, а за формулою (50.7) визначають магнітну проникність m досліджуваного феромагнетика. Побудувавши графік залежності m від Н (див. рис. 50.5), знаходять максимальне значення проникності.
9. ЗАСТОСУВАННЯ ФЕРОМАГНІТНИХ МАТЕРІАЛІВ У залежності від значень коерцитивної сили розрізняють магнітно-тверді (магнітно-жорсткі) та магнітно-м'які матеріали. Магнітно-тверді матеріали характеризуються великим значенням коерцитивної сили (103 А/м – 105 А/м). Для магнітно-м'яких матеріалів коерцитивна сила величина порядку 0.1 – 10 А/м. Тому в тих пристроях, де необхідно перемагнічування феромагнетика використовують магнітно–м'які матеріали. Це стосується осердь трансформаторів, роторів та статорів електродвигунів змінного струму, осердь дроселів змінного струму і т.д. КОНТРОЛЬНІ ПИТАННЯ 1. Дати означення магнітного моменту контуру із струмом. 2. Які магнітні моменти зумовлюють магнітні властивості речовини. 3. Дайте означення намагніченості (вектора намагнічення речовини). 4. Які величини називаються магнітною сприйнятливістю і магнітною проникністю речовини? Який зв’язок між цими величинами? 5. Які речовини називаються діамагнетиками, парамагнетиками і феромагнетиками? Яка для цих речовин магнітна сприйнятливість і магнітна проникливість? 6. Яка природа феромагнетизму? Наведіть та поясність криву намагнічення феромагнетика. 7. В чому полягає магнітний гістерезис? Наведіть та поясніть петлю гістерезису 8. Який принцип експериментального методу зняття петлі гістерезису за допомогою осцилографа? 9. Яка послідовність виконання роботи? Як розрахувати залишкову намагніченість та коерцитивну силу досліджуваного феромагнетика? 10. Наведіть приклади застосування феромагнітних матеріалів. Лабораторна робота № 53 ВИВЧЕННЯ РОБОТИ РЕЛАКСАЦІЙНОГО ГЕНЕРАТОРА
МЕТА РОБОТИ: засвоїти теоретичний матеріал з теми "Релаксаційні коливання” та освоїти методику експериментального визначення опорів резисторів та ємностей конденсаторів за допомогою релаксаційного генератора на неоновій лампі. ПРИЛАДИ: неонова лампа, джерело постійного струму, реостат, вольтметр, набір резисторів та конденсаторів, секундомір.
1. ПОНЯТТЯ ПРО РЕЛАКСАЦІЙНІ КОЛИВАННЯ.
2. СТРУМ В ГАЗАХ. ВИДИ ГАЗОВИХ РОЗРЯДІВ. Гази при звичайних умовах є діелектриками, в них відсутні вільні електричні заряди. Газ стає провідником струму, якщо деяка частина його молекул іонізується. Тобто від нейтральних молекул чи атомів відбираються електрони і тоді молекули (атоми) стають додатними іонами. Проходження струму через газ називається газовим розрядом Розрізняють несамостійний і самостійний газовий розряди. Несамостійний газовий розряд відбувається лише при постійній дії іонізатора. Іонізатором газу може бути термічна дія (нагрів газу), опромінювання ультрафіолетовим світлом, або радіоактивними частинками і т.п. Після припинення дії іонізатора несамостійний газовий розряд в газі припиняється. Строго кажучи, провідність газів не завжди рівна нулю, так як в газах завжди присутня невелика кількість іонів і електронів завдяки дії природний радіоактивного випромінювання Землі, а також космічних променів. Саме така невелика кількість електронів і іонів зумовлює подальший розвиток самостійного газового розряду. Розряд в газах, який продовжується після припинення дії іонізатора називається самостійним і він починається при певній напрузі - напрузі пробою (для неонової лампи - це напруга запалювання). Так, якщо в газі між двома електродами (катодом і анодом) створити електричне поле, то лише при певній напрузі електрони набувають енергії необхідної для іонізації молекул газу. Утворюються вторинні електрони та іони, які знову іонізують молекули газу і т.д. Такий процес має лавиноподібний характер який називається ударною іонізацією. Але ударна іонізація ще недостатня для підтримання самостійного розряду, необхідно, щоб електронні лавини "відтворювались". Це відтворення відбувається за рахунок додатних іонів, які прискорені електричним полем, вдаряючись об катод, вибивають з нього електрони. Крім того, мають місце ще інші процеси, а саме: 1) позитивні іони переводять в збуджений стан молекули газу, що супроводжується випусканням фотонів (газ світиться); 2) утворені фотони вибивають електрони з катода (фотоефект); 3) під дією фотонів можлива фотонна іонізація газу. Якщо тиск в газах незначний (декілька мм.рт.ст.), то самостійний газовий розряд, приймає форму тліючого розряду. Саме такий розряд і спостерігається в неоновій лампі. При більш високих тисках, наприклад, при атмосферному, розряд приймає форму іскрового. Іскри являють собою канали, які заповнені плазмою (іонізованим газом). Ці канали називаються стримерами (від англійського – стрічка). Прикладом іскрового розряду є таке природне явище, як блискавка. Крім того, в газах можливі ще інші види розрядів - дуговий та коронний. Дуговий розряд підтримується за рахунок високої температури катоду, що приводить до інтенсивної термоелектронної емісії, а також за рахунок термічної іонізації молекул газу. Дуговий розряд широко застосовується для зварювання і різки металів. Коронний розряд - високовольтний розряд в різко неоднорідному електричному полі. Наприклад, коли напруженість поля біля гострого вістря досягає 30 кВ/см, то біля цього вістря виникає свічення газу, яке має вигляд, корони, звідси назва - коронний розряд.
3. РЕЛАКСАЦІЙНИЙ ГЕНЕРАТОР НА НЕОНОВІЙ ЛАМПІ.
При досягненні напруги U г, яку називаються напругою гасіння, струм через лампу стрибком спадає до нуля і лампа гасне. Для спрощеного математичного опису релаксаційного генератора на неоновій лампі користуються ідеалізованою вольт-амперною характеристикою лампи (рис. 53.4), де ділянки 1‑2 та 2‑3 співпадають. У відповідності з цією характеристикою внутрішній опір лампи R i є розривною функцією від напруги U. Дійсно, при збільшенні напруги від нуля до напруги запалювання U з опір лампи дорівнює нескінченості R i = ¥ (струм відсутній). В області значень U > U з опір лампи має певне кінцеве значення, яке згідно закону Ома дорівнює
При вмиканні кола спочатку відбувається зарядка конденсатора (неонова
|
||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 836; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.92.50 (0.019 с.) |

 Ряд магнітних властивостей феромагнетиків було встановлено ще в минулому столітті, але розуміння цих властивостей дає лише сучасна квантова фізика.
Ряд магнітних властивостей феромагнетиків було встановлено ще в минулому столітті, але розуміння цих властивостей дає лише сучасна квантова фізика. Спрощено механізм виникнення самих доменів можна пояснити таким чином. Нехай весь феромагнетик являє собою один великий домен, в якому внаслідок обмінної взаємодії всі спінові магнітні моменти орієнтувались в одному напрямі вздовж “найлегшого” намагнічення, наприклад вздовж вісі Y (рис. 49.3а). Такий великий домен по суті, являє собою постійний магніт і в зовнішньому просторі існує магнітне поле, яке володіє певною енергією.
Спрощено механізм виникнення самих доменів можна пояснити таким чином. Нехай весь феромагнетик являє собою один великий домен, в якому внаслідок обмінної взаємодії всі спінові магнітні моменти орієнтувались в одному напрямі вздовж “найлегшого” намагнічення, наприклад вздовж вісі Y (рис. 49.3а). Такий великий домен по суті, являє собою постійний магніт і в зовнішньому просторі існує магнітне поле, яке володіє певною енергією. Коли струм у вторинній обмотці почне зменшуватись, покази знімають через кожну поділку шкали мікровольтметра.
Коли струм у вторинній обмотці почне зменшуватись, покази знімають через кожну поділку шкали мікровольтметра. , де е - заряд електрона, Т - період його обертання. Даний коловий струм створює магнітне поле і магнітний момент Pm електрона, який рухається навколо ядра атома називається орбітальним магнітним моментом і він дорівнює добутку сили струму І на площу орбіти S (50.1). Магнітний момент - вектор, напрям якого визначається за правилом свердлика (рис. 50.1).
, де е - заряд електрона, Т - період його обертання. Даний коловий струм створює магнітне поле і магнітний момент Pm електрона, який рухається навколо ядра атома називається орбітальним магнітним моментом і він дорівнює добутку сили струму І на площу орбіти S (50.1). Магнітний момент - вектор, напрям якого визначається за правилом свердлика (рис. 50.1).
 (50.1).
(50.1). . (50.2)
. (50.2)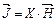 (50.3)
(50.3) (50.4)
(50.4) (50.5)
(50.5) Домени - мікроскопічні області (10-3 - 10-4 мм) спонтанного (самовільного) намагнічення. Механізм виникнення спонтанного намагнічення пояснює квантова фізика, де розглядаються особливі сили обмінної взаємодії, в результаті яких спінові магнітні моменти електронів незаповнених електронних оболонок атомів орієнтуються в одному напрямі. На рис. 50.2 схематично зображена доменна структура феромагнетика, де стрілками вказані напрями магнітних моментів окремих доменів. Напрями цих моментів для різних доменів різні, так, що у відсутності зовнішнього магнітного поля, сумарний магнітний момент всього тіла рівний нулю.
Домени - мікроскопічні області (10-3 - 10-4 мм) спонтанного (самовільного) намагнічення. Механізм виникнення спонтанного намагнічення пояснює квантова фізика, де розглядаються особливі сили обмінної взаємодії, в результаті яких спінові магнітні моменти електронів незаповнених електронних оболонок атомів орієнтуються в одному напрямі. На рис. 50.2 схематично зображена доменна структура феромагнетика, де стрілками вказані напрями магнітних моментів окремих доменів. Напрями цих моментів для різних доменів різні, так, що у відсутності зовнішнього магнітного поля, сумарний магнітний момент всього тіла рівний нулю. Спочатку відбувається зміщення границь доменів, "ростуть" ті домени, магнітні моменти яких складають малі кути з напрямом зовнішнього поля. Далі має місце інший ефект - магнітні моменти доменів повертаються в напрямі зовнішнього поля. Нарешті, коли всі магнітні моменти доменів будуть орієнтовані в напрямі зовнішнього поля, наступає явище магнітного насичення. Подальше збільшення напруженості магнітного поля вже не приводить до збільшення намагніченості. На рис.50.3 наведена крива намагнічення феромагнетика, магнітний момент якого спочатку був рівним нулю. Така крива називається основною або нульовою кривою намагнічення.
Спочатку відбувається зміщення границь доменів, "ростуть" ті домени, магнітні моменти яких складають малі кути з напрямом зовнішнього поля. Далі має місце інший ефект - магнітні моменти доменів повертаються в напрямі зовнішнього поля. Нарешті, коли всі магнітні моменти доменів будуть орієнтовані в напрямі зовнішнього поля, наступає явище магнітного насичення. Подальше збільшення напруженості магнітного поля вже не приводить до збільшення намагніченості. На рис.50.3 наведена крива намагнічення феромагнетика, магнітний момент якого спочатку був рівним нулю. Така крива називається основною або нульовою кривою намагнічення. При вивченні магнітного гістерезису зручно визначити залежність індукції В магнітного поля в феромагнетику від напруженості Н намагнічуючого поля, яке можна змінювати як за величиною, так і за напрямом.
При вивченні магнітного гістерезису зручно визначити залежність індукції В магнітного поля в феромагнетику від напруженості Н намагнічуючого поля, яке можна змінювати як за величиною, так і за напрямом.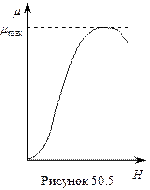 Петлю гістерезису з ділянками насичення називають максимальною. Якщо ж насичення відсутнє, то отримуємо петлю, яку називають частковим циклом (пунктирна петля на рис. 50.4). Індукція магнітного поля В зв’язана з напруженістю Н співвідношенням (50.6), де m0 - магнітна стала (m 0=4×10-7 Гн/м).
Петлю гістерезису з ділянками насичення називають максимальною. Якщо ж насичення відсутнє, то отримуємо петлю, яку називають частковим циклом (пунктирна петля на рис. 50.4). Індукція магнітного поля В зв’язана з напруженістю Н співвідношенням (50.6), де m0 - магнітна стала (m 0=4×10-7 Гн/м). (50.7)
(50.7)

 (50.8)
(50.8) (50.9)
(50.9) (50.10)
(50.10) (50.11)
(50.11) (50.12)
(50.12) (50.13)
(50.13) (50.14)
(50.14) , а на виході отримуємо напругу (50.14), яка пропорційна В.
, а на виході отримуємо напругу (50.14), яка пропорційна В. (50.15)
(50.15) (50.16)
(50.16) (50.17)
(50.17) (50.18)
(50.18) На лабораторному стенді розташовані всі прилади, необхідні для виконання роботи: ЛАТР, тороїд з обмотками, осцилограф, резистори, конденсатор.
На лабораторному стенді розташовані всі прилади, необхідні для виконання роботи: ЛАТР, тороїд з обмотками, осцилограф, резистори, конденсатор. 1. Виміряти віддаль а=2х між двома точками петлі гістерезису (рис.50.7), які відповідають коерцитивній силі Н k. Підставивши
1. Виміряти віддаль а=2х між двома точками петлі гістерезису (рис.50.7), які відповідають коерцитивній силі Н k. Підставивши  в формулу (50.17), розрахувати значення H k.
в формулу (50.17), розрахувати значення H k. і розрахувати значення В3.
і розрахувати значення В3. (50.19)
(50.19) (50.20)
(50.20) Релаксаційні коливання - це коливання, які виникають в нелінійних системах і характерні тим, що складаються з процесів повільного та швидкого змін стану системи. В лінійних системах виконується лінійна залежність однієї величини від іншої. Наприклад, в механіці сила пружності пропорційна деформації F=−kx (закон Гука), а в електриці для металічного провідника сила струму пропорційна напрузі
Релаксаційні коливання - це коливання, які виникають в нелінійних системах і характерні тим, що складаються з процесів повільного та швидкого змін стану системи. В лінійних системах виконується лінійна залежність однієї величини від іншої. Наприклад, в механіці сила пружності пропорційна деформації F=−kx (закон Гука), а в електриці для металічного провідника сила струму пропорційна напрузі  (закон Ома). Якщо ж лінійні залежності порушуються, то маємо нелінійні системи.
(закон Ома). Якщо ж лінійні залежності порушуються, то маємо нелінійні системи.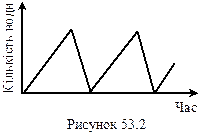 Саме слово "релаксація" з грецького означає послаблення. Прикладом релаксаційних коливань в механіці може бути коливання посудини (рис.53.1), яка наповнюється водою. По мірі наповнення водою посудини її центр мас піднімається і стає вищим вісі обертання ОО. Посудина перевертається, вода виливається і посудина повертається в попереднє положення. Залежність кількості води від часу має характерну пилоподібну форму (рис.53.2), де перший повільний процес 1-2 це накопичення води, а другий 2-3 швидкий процес її зменшення, тобто релаксація (послаблення стану системи). В електриці роль нелінійного елемента, що зумовлює релаксаційні коливання, може грати неонова лампа, в якій і має місце нелінійна залежність сили струму в газі (неоні) від напруги (рис. 53.2). Тому, щоб зрозуміти принцип роботи релаксаційного генератора на неоновій лампі доцільно коротко зупинитись на окремих питаннях механізму провідності газів.
Саме слово "релаксація" з грецького означає послаблення. Прикладом релаксаційних коливань в механіці може бути коливання посудини (рис.53.1), яка наповнюється водою. По мірі наповнення водою посудини її центр мас піднімається і стає вищим вісі обертання ОО. Посудина перевертається, вода виливається і посудина повертається в попереднє положення. Залежність кількості води від часу має характерну пилоподібну форму (рис.53.2), де перший повільний процес 1-2 це накопичення води, а другий 2-3 швидкий процес її зменшення, тобто релаксація (послаблення стану системи). В електриці роль нелінійного елемента, що зумовлює релаксаційні коливання, може грати неонова лампа, в якій і має місце нелінійна залежність сили струму в газі (неоні) від напруги (рис. 53.2). Тому, щоб зрозуміти принцип роботи релаксаційного генератора на неоновій лампі доцільно коротко зупинитись на окремих питаннях механізму провідності газів.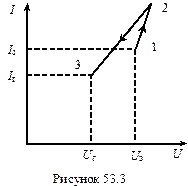 Неонова лампа - газорозрядний прилад, конструктивно виконаний у вигляді скляного балона заповненого неоном при невеликому тиску (10-15 мм.рт.ст.). В балон впаяні два електрода, розташованих на відстані 1-3 мм. Характерною властивістю неонової лампи є те, що вона починає проводити струм при певному значенню напруги між електродами і ця напруга називається напругою запалювання U з. При цій напрузі має місце самостійний розряд в неоні у вигляду тліючого розряду. Напруга запалювання залежить від відстані між електродами, їх форми, а також від тиску і природи газу. Після запалювання лампа може світитись при більш низькій напрузі і гасне при напрузі U г (напруга гасіння). Вольт-амперна характеристика неонової лампи приведена на рис. 53.3. При малих напругах між електродами струм через лампу відсутній, при досягненні напруги запалювання в лампі виникає самостійний розряд і струм стрибком досягає значення I з (струм запалювання). При подальшому збільшенні напруги (ділянка 1‑2) струм в лампі зростає (явища насичення не розглядаємо).
Неонова лампа - газорозрядний прилад, конструктивно виконаний у вигляді скляного балона заповненого неоном при невеликому тиску (10-15 мм.рт.ст.). В балон впаяні два електрода, розташованих на відстані 1-3 мм. Характерною властивістю неонової лампи є те, що вона починає проводити струм при певному значенню напруги між електродами і ця напруга називається напругою запалювання U з. При цій напрузі має місце самостійний розряд в неоні у вигляду тліючого розряду. Напруга запалювання залежить від відстані між електродами, їх форми, а також від тиску і природи газу. Після запалювання лампа може світитись при більш низькій напрузі і гасне при напрузі U г (напруга гасіння). Вольт-амперна характеристика неонової лампи приведена на рис. 53.3. При малих напругах між електродами струм через лампу відсутній, при досягненні напруги запалювання в лампі виникає самостійний розряд і струм стрибком досягає значення I з (струм запалювання). При подальшому збільшенні напруги (ділянка 1‑2) струм в лампі зростає (явища насичення не розглядаємо).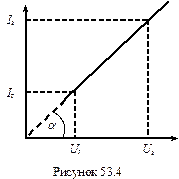 Якщо зменшувати напругу, то зменшення струму характеризується ділянкою 2-3 (яка близька до ділянки 1-2)
Якщо зменшувати напругу, то зменшення струму характеризується ділянкою 2-3 (яка близька до ділянки 1-2)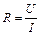 . Значення цього опору чисельно дорівнює ctg a (рис. 53.4).
. Значення цього опору чисельно дорівнює ctg a (рис. 53.4). Принципова схема релаксаційного генератора на неоновій лампі наведена на рис. 53.5. Паралельно до неонової лампи приєднаний конденсатор ємністю С, який заряджається через резистор опором R від джерела постійного струму. Напруга між обкладинками конденсатора вимірюється вольтметром і регулюється потенціометром П.
Принципова схема релаксаційного генератора на неоновій лампі наведена на рис. 53.5. Паралельно до неонової лампи приєднаний конденсатор ємністю С, який заряджається через резистор опором R від джерела постійного струму. Напруга між обкладинками конденсатора вимірюється вольтметром і регулюється потенціометром П.


