
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корпускулярно-хвильова природа електромагнітного випромінюванняСодержание книги
Поиск на нашем сайте Частина V. КВАНТОВА ФІЗИКА КОРПУСКУЛЯРНО-ХВИЛЬОВА ПРИРОДА ЕЛЕКТРОМАГНІТНОГО ВИПРОМІНЮВАННЯ Проблеми випромінювання абсолютно чорного тіла Основні визначення Електромагнітне випромінювання, що виникає за рахунок внутрішньої енергії випромінюючого тіла і залежить лише від температури та оптичних властивостей тіла, називається тепловим випромінюванням. Теплове випромінювання є рівноважним. Помістимо в замкнену адіабатичну оболонку кілька тіл з різними температурами. У відповідності з другим началом термодинаміки в такій системі почнуть протікати процеси, які приведуть до вирівнювання температур тіл. Ці процеси полягають у висиланні та поглинанні електромагнітного випромінювання тілами, що містяться усередині порожнини, і не припиняються після досягнення термодинамічної рівноваги. Це може бути лише в тому випадку, якщо між тілом і випромінюванням установлюється рівновага: скільки енергії випромінює тіло, стільки ж її воно й поглинає. Уведемо деякі кількісні характеристики теплового випромінювання. Випромінювальною здатністю тіла називається кількість енергії, що висилається за одиницю часу з одиниці площі в одиничному інтервалі частот:
Спектральною густиною випромінювання називається кількість енергії електромагнітного випромінювання, що припадає на одиничний інтервал частот і зосереджена в одиничному об'ємі:
Оскільки теплове випромінювання є рівноважним, то між випромінювальною здатністю тіла й спектральною густиною випромінювання повинна існувати пропорційна залежність r(n,T)~u(n,T). Для абсолютно чорного тіла ця залежність має вигляд
де с – швидкість світла у вакуумі. Інтегральною випромінювальною здатністю (енергетичною світністю) називається кількість енергії, що випускається за одиницю часу з одиниці площі у всьому інтервалі частот від 0 до ∞. Між інтегральною випромінювальною здатністю Rе(Т) і випромінювальною здатністю r(n,T) існує зв'язок.
Поглинальною здатністю тіла називається відношення поглиненої енергії до всієї падаючої на тіло енергії в інтервалі частот від n до n+dn:
Абсолютно чорним тілом (АЧТ) називається таке тіло, поглинальна здатність якого для всіх частот і температур дорівнює одиниці: a(n,T)=1. Моделлю АЧТ може служити невеликий отвір, вирізаний в порожній сфері з непрозорої речовини (рис. 29.1). Промінь світла, потрапляючи через такий отвір усередину порожнини, потерпає багаторазові відбиття і практично повністю поглинається.
Сірим називається таке тіло, поглинальна здатність якого менша одиниці, але стала для всіх частот і температур (рис. 29.2). У кольорового тіла (КТ) поглинальна здатність є функцією частоти й температури. Закон Кірхгофа Кірхгоф установив закон, згідно з яким відношення випромінювальної здатності тіла до його поглинальної здатності не залежить від природи тіла і є універсальною функцією від частоти й температури:
Для АЧТ поглинальна здатність дорівнює одиниці, тому для такого тіла випромінювальна здатність збігається з універсальною функцією
Нехай адіабатична оболонка[1], внутрішні стінки якої є АЧТ, заповнена рівноважним тепловим випромінюванням. Виділимо на поверхні оболонки ділянку площею dS і підрахуємо для нього баланс енергії. Із цієї ділянки випромінюється енергія r*(n,T)dS, де r*(n,T) — випромінювальна здатність АЧТ. Для збереження термодинамічної рівноваги стільки ж енергії повинне поглинатися. Оскільки для АЧТ a(n,T) = 1, то з боку інших ділянок на виділений повинна падати енергія, рівна r*(n,T)dS. Замінимо тепер виділену ділянку стінки оболонки деяким довільним тілом, у якого випромінювальна здатність дорівнює ri(n,T), а поглинальна аi(n,T)<1. Складемо тепер баланс енергії для цього випадку. Як і в першому випадку, на цю ділянку буде падати енергія r*(n,T)dS, частина якої аi(n,T)·r*(n,T)dS, буде поглинатися; випромінюватися ж буде енергія, що дорівнює ri(n,T) dS, Оскільки процес рівноважний, то
звідки
Формула (29.7) справедлива для будь-якого тіла – тим самим закон Кірхгофа доведений. Закони випромінювання АЧТ
Основна проблема вивчення АЧТ – визначення виду функції r*(n,T). Експерименти дозволили знайти цю залежність і сформулювати деякі частинні закони випромінювання АЧТ. Експериментальні залежності r*(n,T) для двох значень температури показані на рис. 29.3. Видно, що випромінювальна здатність АЧТ падає при малих і великих частотах і досягає максимуму при деякім значенні nm. З підвищенням температури випромінювальна здатність зростає, а її максимальне значення зміщується в область великих частот. Сформулюємо частинні закони випромінювання АЧТ. 1. Закон Стефана - Больцмана. Інтегральна випромінювальна здатність АЧТ пропорційна до четвертого степеня його абсолютної температури, тобто
де s –стала Стефана - Больцмана. 2. Закон зміщення (Віна). Частота, на яку припадає максимум поглинальної здатності АЧТ, пропорційна до його абсолютної температури:
де b — стала Віна. Закон Віна встановлює положення максимуму кривої r*(n,T): з підвищенням температури максимум зміщується в область більш високих частот. 3. Висота максимуму кривої r*(n,T). Вона встановлюється наступним законом (іноді його називають другим законом Віна): максимальна випромінювальна здатність АЧТ пропорційна до куба його абсолютної температури:
де С — стала. Ці закони, однак, не дають можливості відтворити явний вигляд функції r*(n,T). Для знаходження вигляду цієї функції Д. Релей і Д. Джінс скористалися класичним законом розподілу енергії за ступенями свободи (§ 9.3) і дістали наступний вираз для випромінювальної здатності АЧТ:
де c — швидкість світла; k — стала Больцмана. Формула Релея - Джінса (29.11) добре узгоджується з дослідом в області малих частот, однак в області великих частот ця формула різко розходиться з експериментом (пунктирна лінія на рис. 29.3). Така невідповідність теорії й експерименту дістала назву ультрафіолетової катастрофи. Таким чином, у рамках класичної фізики не вдалося пояснити закономірності теплового випромінювання АЧТ. Причина цього полягає в принциповій незастосовності законів класичної фізики до елементарних процесів, що обумовлюють теплове випромінювання. 4. Формула Планка. В 1900 р. М. Планк висловив гіпотезу, що процес випромінювання та поглинання світла відбувається не безперервно, а певними порціями (квантами), енергія яких визначається формулою
де h = 6,62· 10-34 Дж·с — універсальна константа, яку називають сталою Планка. За допомогою таких квантових уявлень про природу випромінювання Планк знайшов функцію розподілу енергії випромінювання АЧТ за частотою v (Додаток 7):
яка дуже точно відтворює експериментальну криву r*(n,T). За допомогою формули Планка (29.13) можна пояснити всі закономірності випромінювання АЧТ, установлені раніше. Зокрема, в області низьких частот, коли hn/kТ<<1, можна приблизно представити експоненту в (29.13) у вигляді
Підставивши (29.14) в (29.13), одержимо формулу Релея - Джінса. Закон Стефана - Больцмана можна дістати з формули Планка, зінтегрувавши вираз (29.13) за частотою в межах від 0 до ∞:
Для обчислення інтеграла зробимо заміну hn/k=x; звідси n=kTx/h, dn=kTdx/h. Тоді
Ми одержали закон Стефана - Больцмана, причому стала
Закон зміщення Віна можна дістати з формули Планка, прирівнявши першу похідну за частотою до нуля:
Взявши похідну, дістанемо
де
Здобуте рівняння розв’язується методом послідовних наближень і має єдиний корінь x = 2,821. З формули (29.15) випливає
тобто дістали закон Віна зі сталою b;
І нарешті, другий закон Віна дістанемо, якщо підставимо (29.16) у формулу Планка:
5. Пірометрія. Розділ технічних застосувань, що використовують закономірності теплового випромінювання для вимірювання температури нагрітих тіл, називається пірометрією. Пірометри – це прилади для вимірювання температури нагрітих тіл за інтенсивністю їх теплового випромінювання. Основна умова застосовності методів пірометрії полягає в тому, що тіло, температуру якого вимірюють за допомогою пірометра, повинне перебувати в тепловій рівновазі і мати поглинальну здатність, близьку до одиниці. Розрізняють яскравісні, кольорові та радіаційні пірометри. У найпростішому візуальному яскравісному пірометрі зі зникаючою ниткою об'єктив фокусує зображення досліджуваного тіла на площину, у якій розташована нитка (стрічечка) спеціальної лампи розжарювання. Через окуляр і червоний фільтр нитку розглядають на тлі зображення тіла і, змінюючи струм розжарення нитки, домагаються, щоб яскравості нитки й тіла були однакові (нитка стає нерозрізненою на тлі тіла). Шкалу приладу, що реєструє струм розжарення, градуюють звичайно в градусах Цельсія або Кельвіна, і в момент вирівнювання яскравостей нитки й тіла прилад показує так звану яскравісну температуру тіла T я. Для вимірювання температури тіл, які в оптичному діапазоні є сірими, застосовують кольорові пірометри. Цими пірометрами вимірюють яскравість тіла у двох областях спектра — синьої й червоної (наприклад, lc = 0,48 мкм і lч= 0,60 мкм). Шкала приладу градуйована в °С и показує кольорову температуру Tк. Найбільш чутливі радіаційні пірометри, що реєструють сумарне випромінювання тіла. Діяїх заснована на законах Стефана –Больцмана і Кірхгофа. Об'єктив радіаційного пірометра фокусує спостережуване випромінювання на приймач, сигнал від якого реєструється приладом, каліброваним по випромінюванню АЧТ і таким, що показує радіаційну температуру T р. Як приймач використають або термостовпчик (батарею послідовно з'єднаних термопар), або болометр, дія якого заснована на зменшенні опору напівпровідників при їх нагріванні. Вимірювані за допомогою пірометрів температури (яскравісна Tя, кольорова Tк, або радіаційна Tр) перераховуються на підставі законів теплового випромінювання в істинну. Наприклад, істинна T і радіаційна T р температури зв'язані співвідношенням
де a — поглинальна здатність тіла. Методами пірометрії вимірюють температуру в печах і інших нагрівальних установках, температуру розплавлених металів, нагрітих газів, полум’я, плазми. Їх широко використовують в автоматизованих системах контролю й керування температурними режимами різноманітних технологічних процесів. Зовнішній фотоефект Явище взаємодії електромагнітного випромінювання з речовиною, при якому енергія передається безпосередньо електронам речовини, і вони виходять у навколишній простір, називається зовнішнім фотоефектом. Експериментально були встановлені такі закономірності фотоефекту: 1) максимальна енергія фотоелектронів не залежить від інтенсивності світла; 2) максимальна енергія фотоелектронів пропорційна частоті падаючого світла; З) число фотоелектронів пропорційно інтенсивності світла; 4) існує деяке граничне значення частоти n0, яке називається червоною границею фотоефекту – при частоті світла n<n0 фотоефект припиняється; 5) фотоефект практично безінерційний. Ці закономірності не могли бути пояснені з точки зору хвильової природи світла. Згідно з цією теорією енергія фотоелектронів повинна бути пропорційна інтенсивності падаючого світла, а червоної границі взагалі не повинно існувати. Правильна теорія фотоефекту дана. Ейнштейном (1905 р.), що виходив з корпускулярних уявлень про природу світла. Згідно з А. Ейнштейном явище фотоефекту являє собою непружне зіткнення кванта світла (фотона) з одним із електронів речовини, в результаті якого електрон, що одержав надлишкову енергію, може вийти за межі речовини. Закон збереження енергії в цьому процесі описується рівнянням Ейнштейна.
де hn — енергія фотона; А — робота виходу електрона з речовини. З рівняння (29.17) видно, що mv2/2 ~ n, тим самим пояснюється друга закономірність фотоефекту. Існування червоної границі фотоефекту пояснюється тим, що в міру зменшення частоти падаючого світла зменшується також кінетична енергія електронів і при деякій частоті n=n0 mv2/2=0 фотоефект припиняється. Порогову частоту n0 можна знайти з умови hn0=A, звідки
Інтенсивність світла визначається співвідношенням I=Nhn де N— число квантів світла й тому з ростом інтенсивності світла зростає число актів взаємодії фотонів з електронами (і зростає число електронів, що вилетіли, але не їх енергія). Цим пояснюється перша й третя закономірноcті фотоефекту. Рівняння (29.17) описує так званий однофотонний фотоефект, коли електроном поглинається лише один фотон (ймовірність одночасного поглинання електроном двох і більш фотонів настільки мала, що нею можна знехтувати). У зв'язку зі створенням потужних джерел монохроматичного випромінювання (лазерів), був виявлений багатофотонний фотоефект. У цьому випадку електрон може одночасно поглинути не один, а кілька фотонів. Рівняння Ейнштейна для багатофотонного фотоефекту приймає вигляд
При цьому гранична частота зсувається в область малих частот.
Явище зовнішнього фотоефекту знаходить широке застосування в техніці для перетворення світлових сигналів в електричні з наступною їх обробкою. Розглянемо основні типи фотоелектричних приладів, які використовують зовнішній фотоефект. 1. Вакуумні фотоелементи — це фотокатод (найчастіше з лужного металу) і анод, поміщені в прозору колбу, у якій створюється високий вакуум. Переваги цих фотоелементів наступні: строга пропорційність між силою фотоструму та світловим потоком; мала інерційність (t~10-9…10-10 с); відсутність утомних явищ; високий внутрішній опір. Основний недолік — невисока чутливість ~1...10 мкА/лм. Область застосування – точні вимірювання світлових потоків у лабораторних умовах. 2. Газонаповнені фотоелементи відрізняються від вакуумних тим, щоїх балон заповнюється інертним газом при невисокому тиску (P»0,1...1 Па). При проходженні через газ фотоелектронів останні іонізують його атоми що приводить до зростання струму й трохи більш високої чутливості ~10…100 мкА/лм. Газонаповнені фотоелементи також мають строгу пропорційність між світловим потоком і силою струму, а їх інерційність (t~10-9…10-10 с) достатня для більшості практичних застосувань. Внаслідок протікання необоротних процесів адсорбції газу-наповнювача стабільність їх роботи трохи нижча, ніж у вакуумних фотоелементів.
Рис. 29.4 3. Фотоелектронні помножувачі (рис. 29.4). У цих приладах для посилення фотоструму використається явище вторинної електронноїемісії, що складається у вибиванні з металу вторинних електронів при його бомбардуванні прискореними електронами. При попаданні світла на фотокатод К з нього вибиваються електрони, які прискорюються електричним полем при русі до електрода Е1, зарядженому позитивно, і вибивають із нього вторинні електрони. Далі цей процес повторюється на наступних електродах Е2,,Е3,···, ЕN і в результаті в ланцюзі анода виникає значний струм. Чутливість фотопомножувачів досить велика й становить 0,1...1 А/лм. Їхні недоліки: складність конструкції й необхідність використання високих напруг (U ~ 1…1,5 кВ). Область застосування – реєстрація дуже слабких світлових потоків. Ефект Комптона Найбільш наочне уявлення про фотон як частинки проявляється в ефекті Комптона, який полягає в тому, що при взаємодії фотона з вільним (або слабко зв'язаним з атомом) електроном фотон віддає частину своєї енергії електрону. При цьому утворюється розсіяний фотон, імпульс якого становить кут q з напрямком початкового руху. Свої досліди А. Комптон проводив в 1923 р., вивчаючи проходження монохроматичних рентгенівських променів через речовину. Як показали досліди, розсіювання рентгенівських променів відбувається зі зміною їх довжини хвилі, що не залежить від природи речовини, що розсіює, і визначається лише кутом розсіювання. Цими особливостями комптонівське розсіювання принципово відрізняється від класичного (релеєвського) розсіювання, яке, як відомо (§28.4), відбувається без зміни довжини хвилі. Всі особливості ефекту Комптона можна пояснити в рамках квантової теорії, що розглядає процес взаємодії фотона з вільними електронами як пружне зіткнення. На рис. 29.5 показана імпульсна діаграма взаємодії фотона й електрона. Припустимо, що до зіткнення з фотоном електрон перебував у спокої, так що його імпульс p=mv =0, а енергія дорівнює енергії спокою W0=m0c2. Застосуємо до розглядуваного процесу закони збереження імпульсу та енергії:
Тут
а його імпульс p=mv. У рівняннях (29.21) застосовані релятивістські вирази для енергії й імпульсу електрона, оскільки рентгенівські фотони, які використовувалися в дослідах Комптона, надавали електронам релятивістських швидкостей. Опускаючи громіздкі математичні викладки, напишемо відразу кінцевий результат, що випливає з (29.21):
Тут Dl=l¢-l — зміна довжини хвилі фотона при його розсіюванні на електроні на кут q. Величина L=h/m0c називається комптонівською довжиною хвилі електрона. З (29.22) видно, що максимальна зміна довжини хвилі фотона спостерігається при його розсіюванні назад (q=180о). У цьому випадку фотон віддає електрону максимально можливу частину своєї енергії. Результати вимірювань Комптона перебувають у повній відповідності з формулою (29.22). Спектр атома водню за Бором Знайдемо спочатку радіус n-ої стаціонарної орбіти електрона. При русі електрона по колу радіуса r на нього діє доцентрова сила mv2/r, роль якої відіграє сила кулонівської взаємодії ядра та електрона
де e — заряд електрона. Виключаючи з рівнянь (29.24) і (29.26) швидкість v, дістанемо радіус n-ої електронної орбіти
Знайдемо тепер повну енергію атома водню:
де Wk, Wp — відповідно кінетична та потенціальна енергія електрона. Скориставшись співвідношенням (29.26), запишемо
Потенціальну енергію електрона знайдемо як добуток заряду електрона на потенціал електростатичного поля, створюваного ядром:
Тут знак «-» ураховує, що потенціальна енергія взаємодії електрона і ядра є енергією притягання. Підставляючи (29.29) і (29.30) в (29.26), одержуємо повну енергію атома водню
І нарешті, підставимо в (29.31) значення радіуса орбіти з (29.27):
де n=1, 2, …... Видно, що енергія атома може приймати лише дискретні значення. Скориставшись другим постулатом Бора, знайдемо частоту фотона, який випускається при переході атома водню зі стаціонарного стану n з більшою енергією в стан m з меншою енергією:
де R — стала Рідберга;
Формула (29.33) збігається з узагальненою формулою Бальмера (29.23), установленої експериментально на підставі аналізу спектра випромінювання водню. У цьому спектрі різними авторами були виділені серії, у яких положення спектральних ліній у шкалі частот підлягає певним закономірностям. Як випливаєз теорії Бору, кожна із серій виходить із формули (29.33) при певному фіксованому значенні числа т і значеннях n, рівних m+1, m+2, …: серія Лаймана
серія Бальмера
серія Пашена
серія Брекета
серія Пфунда
Рис. 29.8 Схема переходів, що приводять до виникнення серій у спектрі випромінювання атома водню, показана на рис, 29.8. Зауважимо, що лінії серії Лаймана розташовані в ультрафіолетовій, серії Бальмера – у видимій, а лінії інших серій – в інфрачервоній частині спектра, Пояснення лінійчатого спектра випромінювання й поглинання атома водню й інших воднеподібних атомівНе+, Li++тощо була блискучим успіхом теорії Бору. Однак згодом було виявлені принципові труднощі, які неможливо було подолати в рамках цієї теорії: теорія Бора внутрішньо суперечлива – вона не була ні послідовно класичною, ні послідовно квантовою теорією; вона залишала відкритим питання про інтенсивність спектральних ліній; спроби застосувати цю теорію до багатоелектронних атомів не увінчалися успіхом. Проте, в історичному плані теорія Бору зіграла свою позитивну роль як проміжний етап на шляху до послідовної квантової теорії атомних явищ. Елементи квантової механіки Рівняння Шредінгера Для того щоб знайти хвильову функцію y, що характеризує стан мікрочастинки або системи мікрочастинок, необхідно розв’язати хвильове рівняння, що було отримано Э. Шредінгером в 1926 р. Рівняння Шредінгера – основа квантової (хвильової) механіки, так само як рівняння Ньютона – основні рівняння класичної механіки. Як і рівняння Ньютона, рівняння Шредінгера не може бути виведене з інших більш елементарних принципів і вводиться у квантову механіку як постулат. Справедливість рівняння Шредінгера визначається тим, що всі висновки, отримані з його рішень і доступні дослідній перевірці, підтверджувалися. Проте, дамо деяке методичне обґрунтування цього рівняння. Продиференціюємо двічі за координатою x хвильову функцію (30.8):
або
Підставимо замість довжини хвиліl її значення за формулою де Бройля:
Ураховуючи, що
де Wк — кінетична енергія частинки, дістанемо
Замінимо в цьому рівнянні кінетичну енергію частинки на різницю між повною і потенціальною енергією: Wк =W-Wр. Тоді
Останнє рівняння і являє собою одномірне стаціонарне рівняння Шредінгера. Якщо ввести сталу ħ=h/2p, то рівняння (30.13) можна переписати у вигляді
У загальному (тривимірному) випадку рівняння Шредінгера має вигляд
У тих випадках, коли потенціальна енергія системи змінюється з часом, необхідно скористатися більш складним часовим рівнянням Шредінгера:
Тунельний ефект
Розглянемо одномірний випадок розподілу потенціальної енергії за координатою x, схематично зображений на рис. 30.5 (випадок потенціальної сходинки). В області I потенціальна енергія частинки дорівнює нулю і вона може вільно переміщатися з деякою сталою швидкістю та енергією. В області II потенціальна енергія частинки дорівнює Wp. У класичній механіці показано, що якщо кінетична енергія частинки більша висоти потенціального бар’єра (Wк>Wp), то частинка може переміститися з області I в область II і рухатися далі в тому же напрямку (але вже зі зменшеною швидкістю та енергією). Якщо ж Wк<Wp, то частинка не може проникнути в область II, а відіб'ється від бар'єра, змінивши напрямок свого руху на протилежний. Розглянемо тепер квантовомеханічне трактування взаємодії мікрочастинки з потенціальним бар’єром, обмежуючись випадком Wк<Wp. Запишемо рівняння Шредінгера для областей I і II: область I:
область II:
Позначивши
запишемо й розв’яжемо відповідні характеристичні рівняння: для області I:
для області II:
Загальні розв’язки рівнянь Шредінгера мають вигляд: для області I:
для області II:
У рівнянні (30.28) перший доданок описує падаючу хвилю, пов'язану із частинкою, а другий – відбиту хвилю. Розглянемо тепер рівняння (З0.29). Перший доданок у ньому не задовольняє умові скінченності, що накладається на хвильову функцію, тому що при x →∞ і y2 →∞. Щоб ця умова не порушувалася, необхідно покласти А2= 0. Тоді хвильова функція (30.29) приймає вид
а ймовірність знайти мікрочастинку на деякій глибині потенціального бар’єра
У класичній фізиці ймовірність проникнення частинки усередину потенціального бар’єра Wк<Wp дорівнює нулю, оскільки в цьому випадку її кінетична енергія стає від’ємною. Однак у квантово-механічному трактуванні такий процес стає можливим.
Розглянемо тепер одномірний випадок розподілу потенціальної енергії, показаний на рис. 30.6. Ділянка II, у межах якої величина потенціальної анергії більша, ніж в областях I і III, що оточують її, називаєтьсяпотенціальним бар'єром. Нехай ліворуч до потенціального бар'єра підлітає мікрочастинка з енергією Wк<Wp. Відповідно до викладеного ця мікрочастинка може проникнути в глиб потенціального бар'єра й виявитися на його правій границі з імовірністю
де d — ширина бар'єра. Виявившись на правому краї бар'єра, частинка стає вільною і може рухатися далі в попередньому напрямку з тією же швидкістю й енергією, які вона мала, підлітаючи до бар'єра. Явище проходження мікрочастинки через потенціальний бар'єр у випадку, якщо її енергія менша за висоту бар'єра, називають тунельним ефектом. Згідно (30.31) прозорість бар'єра D,тобто ймовірність проходження мікрочастинки через потенціальний бар'єр, визначається виразом
Вираз (30.32) справеджується для потенціального бар'єра найпростішої прямокутної форми, а для бар'єра довільної форми (рис. 30.7) прозорість визначається формулою
З формул (30.32) і (30.33) видно, що ймовірність проходження мікрочастинки через потенціальний бар'єр збільшується в міру зменшення ширини бар'єра та зростання енергії частинки. Розглянемо приклади деяких фізичних явищ, які описуються закономірностями тунельного ефекту. 1. Якщо два провідники розділені шаром діелектрика, то струм через такий контакт протікати не може, однак при малій товщині діелектричного прошарку (d≤10-8 м ) електрони можуть переходити крізь шар діелектрика, створюючи тунельний контакт. Найцікавіший той випадок, коли обидва метали перебувають у надпровідному стані (див. §34.2). 2. На границі між напівпровідниками з електронним і дірковим типами провідності утворюється контактна різниця потенціалів, що створює потенціальний бар'єр для переходу електронів. За певних умов формування контакту стають можливими тунельні переходи електронів через нього (тунельний діод – див. §33.7). 3. На основі тунельного ефекту створений електронний мікроскоп принципово нового типу. У цьому мікроскопі надтонке металеве вістря наближається до досліджуваної поверхні на малу відстань і фіксується тунельний електричний струм, що протікає через розрядний проміжок. При переміщенні вістря дрібні нерівності на досліджуваній поверхні змінюють ширину потенціального бар'єра й, отже, значення сили струму в колі. Прилад настільки чутливий, що дозволяє фіксувати окремі атоми. ФІЗИКА АТОМІВ І МОЛЕКУЛ Рентгенівські спектри Рентгенівські промені — це електромагнітні хвилі з малою довжиною хвилі — l £ 0,1 нм. Рентгенівське випромінювання виникає при бомбардуванні електронами електрода, виконаного з матеріалу, що складається з атомів з z > 20. Розрізняють суцільний і характеристичний (лінійчастий) рентгенівські спектри.
Суцільний рентгенівський спектр (рис. 31.3) виникає при порівняно низькій прискорювальній напрузі в рентгенівських трубках (U ≈ (3...5)×104 В). Форма суцільного рентгенівського спектра нагадує спектр випромінювання АЧТ (див. §29.1), але роль температури грає прискорююча напруга. Принципове розходження цих двох типів спектрів полягає в тому, що спектр суцільного рентгенівського випромінювання обмежений з боку коротких хвиль значенням l0, при якому інтенсивність випромінювання перетворюється на нуль. Зі зростанням напруги значення короткохвильової границі l0 зміщується в область коротких хвиль. Походження суцільного спектра, існування в ньому короткохвильової границі і її залежність від напруги можна пояснити так. При зіткненні з анодом електрон потерпає різке гальмування, тобто рухається з великим від’ємним прискоренням. Відповідно до законів класичної електродинаміки заряд, що рухається прискорено, випромінює електромагнітні хвилі. Строгі розрахунки за теорією Максвелла дозволили знайти аналітичний вираз для залежності I(l), показаної на рис. 31.3. Щоб пояснити існування короткохвильової границі суцільного спектра запишемо закон збереження енергії для взаємодії електрона з анодом. Пройшовши прискорюючу різницю потенціалів U, електрон набуває кінетичну енергію mv2/2=eU, що частково витрачається на випромінювання світлового кванта з енергією hν, а частково перетворюється в теплову енергію, що приводить до розігрівання анода
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 482; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.014 с.) |

 .
.
 .
.


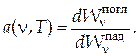
 Рис. 29.1.
Рис. 29.1.
 Рис. 29.2.
Рис. 29.2.
 .
.


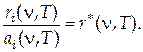
 Рис. 29.3
Рис. 29.3
 .
.
 ,
,





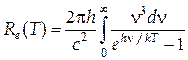





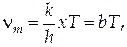
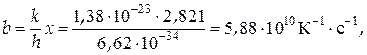
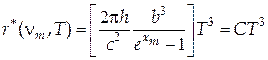



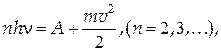


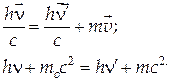
 Рис. 29.5
Рис. 29.5
 і
і  — імпульси фотона до і після взаємодії з електроном. Після зіткнення з фотоном енергія електрона стає рівноюmc2, де маса рухомого електрона
— імпульси фотона до і після взаємодії з електроном. Після зіткнення з фотоном енергія електрона стає рівноюmc2, де маса рухомого електрона































 Рис. 30.5
Рис. 30.5






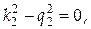



 .
.

 Рис. 30.6
Рис. 30.6



 Рис. 30.7
Рис. 30.7
 Рис. 31.3
Рис. 31.3



