
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Квантово-механічна модель атома воднюСодержание книги
Поиск на нашем сайте
Потенціальна енергія атома водню визначається виразом (29.30), тому рівняння Шредінгера щодо атома водню має вигляд
Хвильова функція y у цьому випадку — це функція трьох просторових координат x, y, z. Розв’язування рівняння (31.1) — досить складне математичне завдання, тому намітимо лише схему розв’язування. Насамперед здійснюють перехід від декартової системи координат (x, y, z) до сферичної (r, q, j) — див. рис. 1.4. У сферичних координатах рівняння Шредінгера (31.1) розбивається на три рівняння, кожне з яких містить лише одну змінну r, q або j. Це в значній мірі спрощує розв’язування задачі, оскільки кожне з отриманих рівнянь – це звичайне диференціальне рівняння. Розв’язавши рівняння відносно r, знаходять значення енергії атома водню. Виявляється, що енергія атома квантується, тобто набуває дискретного ряду значень
Тутn=1, 2, … називається головним квантовим числом. Вираз (31.2) збігається з результатом, отриманим в теорії Бора (29.32), однак при його виведенні не вводилися ніякі додаткові припущення (постулати), як у теорії Бора. Розв’язавши рівняння відносно q, можна знайти момент імпульсу електрона. Виявляється, що допустимі значення моменту імпульсу приймають дискретний ряд значень, що визначається орбітальним квантовим числом l:
Орбітальне квантове число l набуває цілочислових значень в інтервалі від 0 до n–1. Вираз (31.3) формально збігається із правилом квантування орбіт Н. Бора (29.24), однак є дві принципових відмінності. По-перше, у теорії Н. Бора l може приймати будь-які, як завгодно великі значення. У квантово-механічній моделі атома максимальне значення орбітального квантового числа l обмежено головним квантовим числом: при даному n орбітальне квантове число має верхню границю n–1. По-друге, у квантово-механічній моделі є стан, що характеризується значенням орбітального квантового числа l=0. У теорії Бора таке значення l неприпустимо, оскільки при цьому швидкість електрона дорівнює нулю, що суперечить ядерній моделі атома Бора-Резерфорда. Це протиріччя підкреслює неприпустимість описання руху електрона як руху по строго визначеній орбіті. І нарешті, розв’язуючи рівняння Шредінгера щодо координати j, можна знайти проекцію моменту імпульсу на виділений напрямок, наприклад, напрямок зовнішнього магнітного поля
де m — магнітне квантове число, що приймає цілочислові значення в інтервалі, обмеженому орбітальним квантовим числом l: m=–l, -(l-1),…,-1, 0, +1,…, l-1, l. Дискретний характер проекції моменту імпульсу Lz на виділений напрямок одержав назву просторового квантування: у зовнішньому магнітному полі момент імпульсу електрона може приймати лише такі напрямки, проекція яких на напрямок цього поля виражається цілим числом (в одиницях ħ). На рис. 31.1 показані можливі орієнтації вектора
Таким чином, стан електрона в атомі описується трьома квантовими числами n, l, т, значення яких визначають величину енергії, моменту імпульсу та проекції моменту імпульсу на виділений напрямок. Енергія атома водню залежить тільки від головного квантового числа. Деякому значенню цього числа відповідають n можливих значень числа l і 2l+1 значень магнітного квантового числа. Головному квантовому числу п=1 відповідають l=0 і т=0. Одержуємо один стан із хвильовою функцією y100. Головному квантовому числу n=2 відповідають числа l=0,1 і т=–1, 0, +1. У результаті при n=2 виходять чотири стани y200, y21,-1, y210, y211. У загальному випадку довільного n дістаємо n2 різних станів. Всі ці стани характеризуються одним і тим же значенням енергії. Стани з однаковим значенням енергії, але різними квантовими числами l і т називаються виродженими. При накладанні зовнішнього магнітного поля виродження знімається: рівні енергії розщеплюються на ряд близько розташованих підрівней, що спектрально проявляється в розщепленні відповідних спектральних ліній (ефект Зеємана). Аналогічний ефект спричинюється також зовнішнім електричним полем (ефект Штарка).
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 371; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.133.127.131 (0.009 с.) |



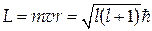 ,
,
 :
: ,
,
 при деяких значеннях орбітального квантового числа l.
при деяких значеннях орбітального квантового числа l. Рис. 31.1
Рис. 31.1



