
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи зонної теорії кристалівСодержание книги
Поиск на нашем сайте
У додатку 8 показано, що при зближенні атомів і утворенні двохатомної молекули енергетичні рівні атомів розщеплюються на два підрівні енергії. Аналогічно можна показати, що при зближенні N атомів і їх об'єднанні в єдине ціле (кристал) внаслідок взаємодії атомів їх енергетичні рівні розщеплюються на N (або більше) близько віддалених підрівнів (рис. 33.1). Таку сукупність підрівнів, що виникла в результаті розщеплення вихідного енергетичного рівня атомів, будемо далі називати дозволеною зоною енергії (або просто дозволеною зоною). Відстані між підрівнями енергії в межах дозволеної зони становлять ~10‑ 23 еВ, що значно менше енергії теплового руху частинок (kT~10-2 еВ). Розподіл електронів за енергетичними підрівнями у межах дозволеної зони визначається принципом мінімуму енергії (відповідно до якого спочатку заповнюються підрівні з меншими значеннями енергії) і принципом Паулі. Розглянемо, наприклад, рівень енергії атома з головним квантовим числом n=1. Цей рівень невироджений, оскільки йому відповідає лише одне значення орбітального квантового числа. При утворенні кристала цей рівень утворює зону, що складається з N підрівнів. У такій зоні відповідно до принципу Паулі може розміститися не більш як 2N електронів. Розглянемо тепер рівень енергії атома з n=2, l=1. Такий рівень енергії трикратно вироджений, оскільки орбітальному квантовому числу l=1 відповідають значення магнітного квантового числа: m=–1, 0, +1. У кристалі виродження знімається: утворюється 3N підрівнів енергії. Отже, максимальне число електронів, які можуть розміститися в зоні, породженої рівнями енергії атома з n=2, l=1, дорівнює 2×3N = 6N. Аналогічно аналізують і інші зони. Зони в кристалі можуть бути не заповненими електронами, заповненими повністю або частково. Результат заповнення залежить від того, яким рівнем енергії атома породжена зона. Розглянемо різні випадки. Нехай на рівні енергії атома із квантовими числами n=1, l=0 перебувають два електрони із протилежними спінами. Якщо в кристалі є N атомів, то у відповідній зоні буде N підрівнів, на кожному з яких розміститься по два електрона (усього 2N електронів). Таким чином, у цьому випадку вийде повністю заповнена зона. Якщо на рівні атома з n=2, l=0 (як, наприклад, в атома літію) перебуває один електрон, то в кристалі з N атомів буде N електронів. Усього ж підрівнів у зоні — 2N. Тому така зона буде заповнена наполовину.
Незаповнена (порожня) зона утвориться в тому випадку, якщо на відповідному рівні енергії атома немає жодного електрона. Електричні властивості твердих тіл визначаються взаємним розташуванням заповнених, частково заповнених і порожніх зон. Залежно від конкретної ситуації тверде тіло має різні електричні властивості. На основі зонної теорії всі тверді тіла за їх електричними властивостями можна розбити на три основні групи: метали, діелектрики та напівпровідники. Тверде тіло можна віднести до однієї із цих груп залежно від розташування валентної зони й зони провідності. Валентною зоною (ВЗ) називається найвища з повністю заповнених електронами зон (рис. 33.2). Наступна зона після валентної називається зоною провідності (ЗП). Зона провідності може бути або частково заповненою електронами, або незаповненою (рис. 33.2, а,б). Рис. 33.2
Електричні властивості твердих тіл визначаються взаємним положенням валентної зони та зони провідності, а також тим, порожня зона провідності чи заповнена частково. У зв'язку із цим немає необхідності розглядати всі зони кристала, досить розглянути зазначені. Якщо зона провідності частково заповнена електронами, то ми маємо справу з металами (рис. 33.3). Розглянемо випадок, коли зона провідності порожня. Електрони перебувають у валентній зоні, що відділена від зони провідності валентною зоною. Залежно від ширини заборонної зони розрізняють діелектрики й напівпровідники. Чіткої границі в такій класифікації немає. Прийнято вважати, що тверде тіло є діелектриком, якщо ширина заборонної зони DW > 4 еВ; якщо ж DW < 4 еВ, те таке тіло відноситься до напівпровідників.
Рис. 33.3 Діелектрики У діелектриків валентна зона повністю заповнена електронами і відділена від зони провідності заборонною зоною, ширина якої DW > kT. У зоні провідності електронів немає, оскільки енергії теплового руху недостатньо для переведення їх з валентної зони в зону провідності. При накладенні зовнішнього електричного поля електрони, що перебувають у валентній зоні, не можуть прийти в спрямований рух, оскільки при цьому їх енергія повинна зрости й, отже, повинні здійснюватися переходи на більш високі підрівні. Однак всі підрівні енергії у валентній зоні зайняті електронами, тому в силу принципу Паулі такі переходи заборонені.
Єдина можливість для виникнення струму провідності в діелектрику – це перехід електрона в зону провідності. Однак, якщо ширина заборонної зони DW >> kТ, то концентрація електронів у зоні провідності така мала, що нею можна знехтувати. Тому діелектрики практично не проводять електричний струм. Розглянемо тепер теплоємність кристала діелектрика. В §10.3 відзначалося, що при не занадто низьких температурах атомна теплоємність кристала дорівнює 3R (закон Дюлонга і Пті). Експерименти показують, що в області низьких температур закон Дюлонга і Пті порушується: при T→0 атомна теплоємність C→0. Причина такого відступу від закону Дюлонга і Пті полягає в тому, що класичний вираз для енергії коливального руху атома ( Кожний атом кристала може виконувати коливання із частотами n, 2n, 3n,..., які можна знайти з виразу (30.25). Завдяки пружним зв'язкам між атомами коливання якого-небудь атома не локалізовані, а поширюються в кристалі у вигляді пружних хвиль тієї ж частоти. Поширення таких пружних хвиль у кристалі можна описувати як рух деяких уявлюваних частинок (квазічастинок), які називаються фононами. Фонон як квазічастинка багато в чому проявляє подібні властивості з реальною частинкою фотоном. Фонони, як і фотони, мають дискретний набір енергій hn, 2hn, 3hn,..., однак, на відміну від фотона фонон може існувати, лише рухаючись усередині кристала. Фонону, як і фотону, приписується цілочисловий спін, що дорівнює одиниці, тому ці частинки належать до бозонів і підлягають статистиці Бозе-Ейнштейна. Використовуючи цю статистику, можна показати, що середня енергія фонона, що доводиться на один ступінь свободи,
Враховуючи, що фонон має три ступені свободи, дістанемо, що внутрішня енергія одного кілограм-атома кристала дорівнює добутку числа Авогадро NA на
Розглянемо поводження внутрішньої енергії U і атомної теплоємності CV в області високих і низьких температур. Область високих температур: hn<<kТ. Тоді
тому вираз для внутрішньої енергії (33.1) приймає вигляд
Звідси атомна теплоємність
тобто у цій області температур справедливий закон Дюлонга й Пті. Область низьких температур: hn>>kТ. Тоді
звідси атомна теплоємність
Оскільки показникова функція e-hn/k при зміні аргументу змінюється істотно швидше, ніж степенева (T-2), неважко показати, що при T → 0, CV → 0. Графік залежності CV від T показано на рис. 33.4. В області низьких температур отримана нами залежність CV(T) — формула (33.2) — лише якісно погодиться з експериментом. Більш струга теорія, що враховує взаємодію фононів, була розроблена Дебаєм.
Метали
На рис. 33.5, а схематично показане заповнення електронами зони провідності для лужного металу (літію) при T = 0. Видно, що в цьому випадку електрони заповнюють всі нижні підрівні енергії аж до деякого рівня WF, який називають рівнем Фермі. При T > 0 частина електронів може переходити на більш високі рівні (рис. 33.5, б).
У частково заповненій зоні провідності металу електрони можуть переходити на більш високі рівні енергії не тільки за рахунок теплового руху, але й під впливом зовнішнього електричного поля, що приводить електрони в упорядкований рух. Ці переходи можливі, оскільки підрівні енергії в зоні розташовані дуже близько один до одного й не заповнені електронами. У зв'язку із цим метали є добрими провідниками. Розглянемо тепер питання про теплоємність металів. Відповідно до класичної теорії атомна теплоємність металів повинна бути вища, ніж у діелектриків, оскільки вільні електрони, що перебувають у металі (електронний газ) повинні мати додаткову теплоємність. Однак експериментально показано, що атомна теплоємність металу дорівнює атомної теплоємності діелектриків. Для з'ясування причин такої розбіжності викладемо класичну й квантову теорії теплоємності електронного газу. Відповідно до класичних уявлень середня кінетична енергія руху електронів має дорівнювати
де NA — число Авогадро. Теплоємність електронного газу
у той час як експеримент показує, що Cел=0
Причина такої розбіжності полягає в тому, що в тепловий рух утягуються не всі електрони, а тільки та їхня частина, енергія яких відрізняється від енергії Фермі на величину ± kТ. Ці електрони заповнюють енергетичний інтервал шириною 2kТ: від WF - kТ до WF +kТ (рис. 33.6). Електрони, що заповнюють нижні підрівні енергії, не можуть збільшити свою енергію, оскільки більш високі підрівні енергії зайняті, а перехід туди ще одного електрона заборонений принципом Паулі. Такі електрони в тепловому русі не беруть участі. Нехай N — число електронів, що перебувають в енергетичному інтервалі шириною 2kТ поблизу рівні Фермі, а NA — загальне число вільних електронів в 1 кг-атомі металу (при T=0 ці електрони заповнюють енергетичний інтервал від 0 до WF). Розв’язуючи пропорцію N — 2k; NA — WF,
знаходимо число електронів, що приймають участь у тепловому русі:
Внутрішню енергію цієї частини електронного газу знайдемо, помноживши N на середню енергію теплового руху електрона:
Тоді теплоємність електронного газу
Як показують розрахунки, енергія Фермі для металів WF ~ 10 еВ. Цій енергії відповідає так звана температура Фермі TF = WF/k~105 К.
Перетворимо (33.3) до вигляду
Тоді з урахуванням того, що T/TF << 1 для будь-яких температур нижче температури плавлення металу, доходимо висновку, що в повній згоді з експериментом C ел = 0. На закінчення розглянемо сучасне квантово-механічне трактування залежності опору металу від температури. Як і в класичній теорії електропровідності, при квантово-механічному розгляді руху електронів у металі виявляється справедливим вираз (15.29) для питомого опору r. У рамках класичної теорії теплопровідності передбачалося, що У квантовій теорії металів енергія електронів Напівпровідники У напівпровідників ширина заборонної зони менша, ніж у діелектриків і становить від 0,1 до 3...4 еВ. У зв'язку з цим енергії теплового руху при кімнатній температурі достатньо для переведення частини електронів з валентної зони на нижні підрівні зони провідності. Під впливом зовнішнього електричного поля енергія електронів у зоні провідності може збільшуватися, оскільки вони можуть переходити на більш високі вакантні підрівні енергії. У результаті виникає електронна провідність (провідність n-типу). При переході частини електронів з валентної зони в зону провідності у валентній зоні утворюються незайняті підрівні («вакансії») і в разі накладання зовнішнього електричного поля електрони, що перебувають у валентній зоні, можуть набувати упорядкованого руху, займаючи вакансії. Такий механізм провідності зручно описувати як рух позитивних зарядів («дірок»). Провідність, обумовлена напрямленим рухом дірок, називається провідністю p-типу. Таким чином, у чистому напівпровіднику провідність має змішаний електронно-дірковий характер. Знайдемо залежність електропровідності провідника від температури. Концентрація електронів у зоні провідності пропорційна ймовірності знаходження їх у цій зоні, тобто функції розподілу Фермі-Дірака (32.2):
Як показують розрахунки, рівень Фермі в чистому напівпровіднику при T=0 К розташований посередині заборонної зони. Зауважимо, що з підвищенням температури рівень Фермі зміщується до зони провідності, однак цей ефект ураховувати не будемо. Якщо відраховувати енергію від стелі валентної зони, то W – WF = DW/2, де DW — ширина заборонної зони. Зонна схема напівпровідника, а також функція розподілу Фермі-Дірака при різних температурах показані на рис. 33.7.
Рис. 33.7 Оскільки електропровідність γ пропорційна концентрації електронів n, то
В області низьких температур (T → 0)
В області кімнатних температур значення експоненти
тобто з ростом температури електропровідність напівпровідників зростає. Механізм такого росту пов'язаний зі збільшенням концентрації вільних електронів (електронів, що перебувають у зоні провідності) при зростанні температури. Зростання електропровідності напівпровідників з температурою досить значне (2-5 % на 1 К), що дозволяє використовувати напівпровідникові опори (термістори) для вимірювань, контролю й регулювання температури. Переваги напівпровідникових датчиків температури такі: їх малі розміри й відповідно мала теплова інерція, високий опір, що дозволяє знехтувати опором підвідних проводів. Такі датчики відрізняються високою чутливістю, що дозволяє використовувати відносно грубі прилади. Недоліки термісторів (властиві, загалом кажучи, всім напівпровідниковим приладам): розкид параметрів у межах партії, у зв'язку із чим виникає необхідність індивідуального приладжування схеми, і зміна параметрів з часом – старіння.
Розглянемо тепер вольт-амперну характеристику термістора (рис. 33.8). На початковому етапі вольт-амперна характеристика лінійна й описується законом Ома. Джоулева теплота, що виділяється при проходженні струму, устигає виділятися в навколишнє середовище, і температура термістора залишається сталою, незначно відрізняючись від температури навколишнього середовища. У міру зростання сили струму виділення джоулевої теплоти протікає більш інтенсивно й при деякім значенні струму I* відбувається різке зростання температури термістора. При цьому опір його падає, що приводить до додаткового зростання струму. Критичне значення струму I* визначається умовами тепловіддачі термістора (ступенем його термоізоляції й температурою навколишнього середовища). З підвищенням температури навколишнього середовища (або з поліпшенням термоізоляції) значення I* зменшується. Явище різкого зростання сили струму в термісторі при перевищенні значення I* називається релейним ефектом і застосовується в системах температурної сигналізації (наприклад, пожежної).
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 362; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.21.145 (0.012 с.) |

 Рис. 33.1
Рис. 33.1


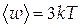 , див. §10.3) при низьких температурах порушується й повинен бути замінений на більш загальний квантово-механічне вираз. Щоб одержати цей вираз, розглянемо більш докладно особливості коливань атомів кристала.
, див. §10.3) при низьких температурах порушується й повинен бути замінений на більш загальний квантово-механічне вираз. Щоб одержати цей вираз, розглянемо більш докладно особливості коливань атомів кристала.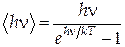 .
.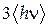 :
: .
.
 ,
, .
. ,
, ,
, ,
, .
.
 Рис. 33.4
Рис. 33.4
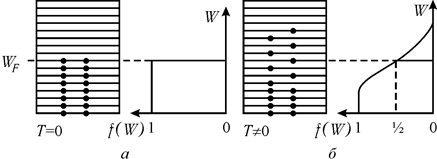 Рис. 33.5
Рис. 33.5
 , тому внутрішня енергія електронів, що містяться в 1 кг-атомі металу,
, тому внутрішня енергія електронів, що містяться в 1 кг-атомі металу, ,
, ,
,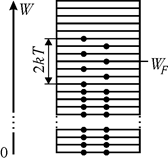 Рис. 33.6
Рис. 33.6
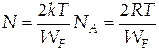 .
. .
. .
.
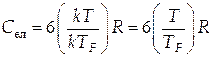 ,
,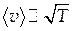 й, отже, питомий опір
й, отже, питомий опір  , що суперечить експерименту, де спостерігається лінійна залежність опору металів від температури.
, що суперечить експерименту, де спостерігається лінійна залежність опору металів від температури.
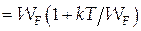 Оскільки
Оскільки  , то енергія електронів і, отже, швидкість їх теплового руху практично не залежить від температури. Залежність же питомого опору металів від температури пояснюється зменшенням середньої довжини вільного пробігу електронів від температури (
, то енергія електронів і, отже, швидкість їх теплового руху практично не залежить від температури. Залежність же питомого опору металів від температури пояснюється зменшенням середньої довжини вільного пробігу електронів від температури (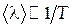 ), що пов'язане з більш ефективним розсіюванням електронів на теплових коливаннях іонів кристалічної гратки при більш високих температурах.
), що пов'язане з більш ефективним розсіюванням електронів на теплових коливаннях іонів кристалічної гратки при більш високих температурах. .
.
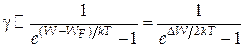 .
.
 , тому
, тому  , тобто при низьких температурах провідник поводиться як діелектрик.
, тобто при низьких температурах провідник поводиться як діелектрик. скінченне і значно більше за одиницю. Тому, нехтуючи одиницею в знаменнику (33.4), дістанемо
скінченне і значно більше за одиницю. Тому, нехтуючи одиницею в знаменнику (33.4), дістанемо ,
, Рис. 33.8
Рис. 33.8



