
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Визначення питомого заряду електрона методом магнетронаСодержание книги
Поиск на нашем сайте
ПРИЛАДИ: універсальне джерело струму; соленоїд; магнетрон; амперметр.
В цій роботі питомий заряд електрона (відношення заряду електрону до його маси) визначається за допомогою методу, який називається «метод магнетрона». Ця назва пов’язана з тим, що конфігурація електричного й магнітного полів, яка використовується у роботі нагадують конфігурацію полів у магнетронах - генераторах електромагнітних коливань в області надвисоких частот. Рух електрона в цьому випадку відбувається в кільцевому просторі, що знаходяться між катодом та анодом двохелектродної електронної лампи (рис. 9.1). Нитка розжарення лампи (катод) розташовується вздовж осі циліндричного аноду так, що електричне поле має радіальний напрямок. Лампа знаходиться у середині соленоїду, який створює магнітне поле, паралельне осі лампи. Розглянемо траєкторію електронів, які рухаються у лампі під дією електричного й магнітного полів. Для обчислення будемо користуватися циліндричною системою координат, тобто будемо характеризувати положення точки спостереження відстанню від осі циліндра r, полярним кутом
Так як магнітне поле в нашому випадку спрямовано по осі z, для проекції сили Лоренца
Інші компоненти сили знайдемо за допомогою формули Лоренца.
Розглянемо тепер сили, які діють на електрон зі сторони магнітного поля.
Із простих кінематичних міркувань видно, що
Рис. 9.1. Схема будови двохелектродної лампи.
Таким чином, ні магнітні, ні електричні сили, які діють на електрон, не мають складової по осі z. Рух по осі z є рівномірним. Рух у площині (r, j) зручно описувати за допомогою рівняння моментів
де L -момент імпульсу відносно осі z, який дорівнює mr2
Підставляючи (9.4) і (9.6) у (9.5), знайдемо
Інтегруючи рівняння (9.7) та пам'ятаючи, що заряд електрону негативний, одержимо:
де А - стала інтегрування, яку слід визначити із початкових умов. В момент вильоту електрону з катоду координата r дорівнює радіусу нитки катода rк, що має достатньо мале значення. Оскільки r входить в
Розглянемо тепер подальший рух електрону вздовж радіусу. Робота сил електричного поля, яка здійснюється при переміщені електронів від катоду до точки з довільним потенціалом U, дорівнює W=eU. Магнітне поле при цьому ніякої роботи не здійснює. Знайдена робота повинна дорівнювати кінетичній енергії електрону (початковою швидкістю електрону ми знов знехтуємо) вважаючи, що в момент вильоту він мав швидкість u = 0. В цьому випадку:
За допомогою (9.4) та (9.9)
Рівняння (9.10) повністю визначає радіальний рух електрону. Розглянемо траєкторію електронів, які вилітають з катоду. Нехай потенціал аноду дорівнює Ua. У відсутності магнітного поля (рис. 9.2.) траєкторія електрону прямолінійна та спрямована вздовж радіусу. При слабкому полі траєкторія трохи викривляється оскільки в кожній точці траєкторії на електрон діє пара взаємо перпендикулярних сил: При деякому критичному значенні індукції магнітного поля Вкр траєкторія викривляється настільки, що електрон тільки торкається аноду, але залишається на ньому. Нарешті при В>Вкр всі електрони зовсім не попадають на анод та повертаються до катоду. В цей момент струм І а зникає, тобто І а =0. Величину Вкр легко знайти за допомогою (9.10).
а) б)
Рис. 9.2. Траєкторія електронів, які вилітають з катоду, при різних значеннях індукції магнітного поля.
Необхідно відмітити, що в цьому випадку радіальна швидкість електрону
Перетворюючи (9.11),знайдемо
Формула (9.12) дозволяє обчислити e/m, якщо при заданому Ua знайдено таке значення магнітного поля (або навпаки, при заданому В таке значення Ua), при якому електрони перестають попадати на анод, тобто Іа = 0. В попередніх викладах передбачалося, що всі електрони, які покидають катод, мають початкову швидкість, що дорівнює нулю. В цьому випадку при B<Bkp всі електрони попадали б на анод, а при B>Bkp всі вони поверталися б на катод, не досягши аноду. Анодний струм Ia зі збільшенням магнітного поля змінювався при цьому б так, як це зображено на рис. 9.3. штрихованою лінією.
Насправді електрони, які випромінюються нагрітим катодом, мають різні початкові швидкості. Критичні умови досягаються при цьому для різних електронів при різних значеннях В. Крива Ia=Ia(B ) набуває внаслідок цього вид суцільної лінії на рис. 9.3, тобто струм Іа зменшується плавно.
Рис. 9.3 Залежність анодного току від індукції магнітного поля. Необхідно зазначити, що в реальних конструкціях неможливо забезпечити повну коаксіальність аноду та катоду. Крім того, в реальних умовах вектор індукції магнітного поля завжди трохи нахилений по відношенню до катоду. Всі ці причини приводять до додаткового згладжування кривої (рис.9.3). Разом з тим в якісно зібраній установці перелом функції Ia=Ia(B) залишається, і є, достатньо різким, тобто може бути використаний для вимірювання та знаходження значення Вкр.
Експериментальна установка
Рис. 9.4. Схема експериментальної установки.
Схема експериментальної установки на базі двохелектродної лампи Л з циліндричним анодом, спеціально виготовленої з немагнітних матеріалів приведена на рис. 9.4. Анод лампи складається з трьох металевих циліндрів однакового діаметру. Два крайніх циліндра, електрично ізольовані від середнього невеликими зазорами. Це використовується для компенсації крайових ефектів на торцях середнього циліндру, струм з якого вимірюється. Замість катоду використовується тонкий (діаметром 50 мкм) добре натягнутий вольфрамовий дріт, розташований по осях всіх трьох циліндрів анодної системи. Катод лампи розігрівається струмом від стабілізованого джерела струму. З цього джерела на анод лампи подається стала напруга (12-120В), яка регулюється за допомогою потенціометра та вимірюється вольтметром. При вимірюваннях лампу вставляють у соленоїд. Струм, який проходить через соленоїд, вимірюється амперметром А. Індукція магнітного поля у соленоїді розраховується по струму, який протікає через обмотку соленоїду. Залежність індукції магнітного поля від струму соленоїда визначається таким чином. По визначенню, індуктивність дорівнює:
L = Ф / I, (9.13)
де - Ф = NBS - повний потік магнітної індукції; N - кількість витків; S - площа витка; I - струм через соленоїд. З другого боку, індуктивність соленоїду можна знайти за виразом
L = mm0N2S / l, (9.14)
де l - довжина соленоїду. З (9.13) та (9.14) можна отримати
B = mm0NI / l (9.15)
Данні для обчислення: N = 2500, l = 168 мм, ra = 3 мм, m 0 = 4p10-7 Гн/м, m = 1
Завдання 1. Увімкнути джерело струму лампи. Встановити на аноді лампи потенціал U a=40В. Зняти залежність анодного струму Ia від індукції магнітного поля В у соленоїді. 2. Зняти таку ж залежність Ia=Ia(B) для 5-6 фіксованих значень Ua у діапазоні 40-120 В. 3. Використати отримані результати для накреслення сімейства кривих Ia(B). По графіку для кожного значення Ua визначити критичне значення індукції магнітного поля Bkp. 4. Накреслити на графіку залежність Bkp2 від Ua. По кутовому коефіцієнту отриманої прямої визначити питомий заряд електрону e/m.
Дані вимірювання занести в таблицю:
Контрольні питання.
1. Які сили діють на електрон у експериментальній установці по визначенню питомого заряду електрону за допомогою методу «магнетрона»? 2. Як описується рух електрону в двохелектродній лампі в площині, перпендикулярній катоду при вимірюванні відношення e/m? 3. Яким чином описується радіальний рух електрону в двохелектродній лампі у «методі магнетрона»? 4. Який вигляд траєкторії електронів при B < Bkp, B = Bkp, B > Bkp в магнетроні? 5. Як визначається відношення e/m в «методі магнетрона»? 6. По якій траєкторії рухається заряд в магнітному полі при довільному напрямку початкової швидкості?
Література.
1. Сивухин Д.В. Общий курс физики. - М.: Наука, 1983, п. 98. 2. Парсел Е. Электричество и магнетизм. - М.: Наука, 1983, гл. 4, п. 4 - 6; гл. 6, п. 9. 3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. - М.: Наука, 1983.
Лабораторна робота № 10
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 912; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.007 с.) |

 та зміщенням вздовж осі z (рис. 9.1). Розглянемо спочатку сили, які діють на електрон зі сторони електричного поля. Напруженість електричного поля у циліндричному конденсаторі має тільки радіальну компоненту E r. Тому сила, яка діє на електрон
та зміщенням вздовж осі z (рис. 9.1). Розглянемо спочатку сили, які діють на електрон зі сторони електричного поля. Напруженість електричного поля у циліндричному конденсаторі має тільки радіальну компоненту E r. Тому сила, яка діє на електрон  у такому полі, спрямована по радіусу, так що
у такому полі, спрямована по радіусу, так що . (9.1)
. (9.1) на вісь z маємо:
на вісь z маємо: . (9.2)
. (9.2) . (9.3)
. (9.3)
 (9.4)
(9.4)
 (9.5)
(9.5) . Величина M z дорівнює rFj. За допомогою (9.1) та (9.3) знайдемо
. Величина M z дорівнює rFj. За допомогою (9.1) та (9.3) знайдемо (9.6)
(9.6) (9.7)
(9.7) (9.8)
(9.8) лівої частини рівняння (9.8), а також в його праву частину то можна стверджувати, що А=0. З урахування сталої А=0 наше рівняння набуде простого вигляду:
лівої частини рівняння (9.8), а також в його праву частину то можна стверджувати, що А=0. З урахування сталої А=0 наше рівняння набуде простого вигляду: (9.9)
(9.9)
 (9.10)
(9.10) , та
, та  , рівнодіюча яких
, рівнодіюча яких 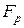 і відхиляється від початкової траєкторії. Однак електрон все ж таки попадає на анод.
і відхиляється від початкової траєкторії. Однак електрон все ж таки попадає на анод.

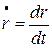 при r=r a (при радіусі анода) обертається у нуль:
при r=r a (при радіусі анода) обертається у нуль: (9.11)
(9.11) (9.12)
(9.12)




