Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вивчення затухаючих коливань у коливальному контурі.Содержание книги
Похожие статьи вашей тематики
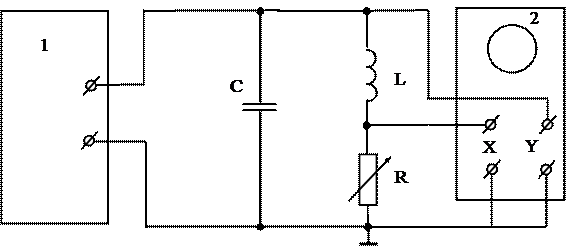
Поиск на нашем сайте ПРИЛАДИ: осцилограф; магазин опорів, макет схеми коливального контуру; генератор імпульсів. В роботі вивчаються вільні коливання у коливальному контурі, який складається з котушки індуктивності L, ємності С та резистора R (рис.6.1).
Рис. 6.1. Коливальний контур.
Конденсатор контуру заряджається короткими одиночними імпульсами, після цього в контурі виникають вільні коливання. Напруга на конденсаторі вивчається за допомогою осцилографа. По рисунку, який з’явився на екрані осцилографічної трубки, можна визначити період електричних коливань в контурі, дослідити процес затухання коливань і визначити основні параметри коливального контуру. Ознайомлення з властивостями коливального контуру та вимірювання його характеристик складають мету роботи. 1. Позначимо через q заряд на конденсаторі, через U напругу на ньому, а через I - струм контуру. З рис. 6.1 ясно, що напруга на конденсаторі дорівнює сумі падінь напруг на резисторі R та котушці індуктивності L:
U = IR+LdI/dt. (6.1)
Заряд конденсатора q пов’язаний зі струмом I явним співвідношенням:
I = -dq/dt. (6.2)
Якщо скористуватись рівнянням q = CU,де С – ємність конденсатора, і підставити його в (6.2), то можна знайти:
I = -d(CU)/dt = -CdU/dt. (6.3) Підставляючи цей вираз (та знайдене з нього значення dI/dt) у рівняння (6.1), отримаємо диференційне рівняння, що описує коливальні процеси в контурі:
Поділимо це рівняння на LC і введемо заміну:
w02 = 1 /LC, та d = R/2L. (6.4)
Величини w 02і d дійсні та позитивні; за знаком мають розмірність частоти, а d називається затуханням контуру (див. нижче). Кінцевий результат отримаємо у вигляді:
Рівняння (6.5) є лінійним диференційним рівнянням другого порядку і описує широкий клас коливальних систем, як електричних, так і механічних. Будемо шукати його рішення у вигляді:
U = A el t. (6.6)
Підставляючи (6.6) в (6.5) та скорочуючи отримане рівняння на A elt, отримаємо: l2+2dl+w02 = 0 (6.7)
Рівняння (6.7) є характеристичним. Воно має два можливих рішення l. l1,2 = - d
Загальне рішення (6.5) може бути записано у вигляді
U = A1
В дане рівняння входять дві сталі А 1 і А 2, вибір яких залежить від початкових умов, наприклад від початкових значень В залежності від співвідношення d і w 0 напруга на конденсаторі U може змінюватись за часом по гармонічному чи аперіодичному закону. 2. Коливальний процес має місце при w 0 > d. З формули (6.8) витікає, що l 1,2 в цьому випадку комплексні. Введемо заміну:
Формула (6.8) набуває вигляду:
Формулу (6.9) зручно записати у вигляді
Обидві формули (6.11) еквівалентні. Вони містять дві довільні сталі: А 1 і А 2 у першому, та B і q - в другому рівнянні.. Легко знайти формули, які зв’язують А 1 та А 2 з константами В та q:
Аргумент (wt - q) є фазою коливань, а коефіцієнт При w0 < d обидва корні рівняння (6.8) дійсні та від’ємні. Розряд носить аперіодичний характер. Як видно з (6.9), напруга на конденсаторі дорівнює сумі двох експонент, спадаючих з різними сталими часу:
4. При w0 = d обидві експоненти будуть тотожні, і залишається всього одна довільна стала А 1 + А2, за допомогою якої неможливо задовольнити початковим умовам задачі. Це доказує, що рішення (6.9) в цьому випадку не буде загальним. При w0 = d загальне рішення має вигляд:
де А і В - довільні сталі. Підставляючи (6.12) в (6.5), легко впевнитись в тому, що при будь-яких значеннях А і В вираз (6.12) дійсно є рішенням (6.5) (при w 0 = d). Режим коливань, що описується формулою (6.12) носить назву критичного. Порівнюючи w 0 і d із (6.4), отримаємо:
Формула (6.13) визначає критичний опір контуру. При 5. В коливальному режимі контур прийнято характеризувати періодом коливань, добротністю і логарифмічним декрементом затухання. Період коливань Т визначається по очевидній формулі, що виходить з (6.10) та (6.11):
Найбільшим практичним інтересом користуються контури зі слабким затуханням. В цьому випадку
Добротність контуру Q показує, в скільки разів запас коливальної енергії в контурі перевищує середню втрату енергії за час, коли фаза коливань змінюється на 1 радіан. Коливальну енергію в контурі легше всього визначити в момент, коли вона знаходиться в конденсаторі, тобто при
Втрата енергії за період дорівнює:
Середня втрата енергії
В цьому випадку добротність Q дорівнює
При написанні ряду формул (6.16) була використана формула (6.15) для періоду і формули (6.4) для частоти власних коливань Логарифмічний декремент затухання
На практиці для визначення корисно використовувати відношення амплітуд, розділених цілим числом періодів п. В цьому випадку формула для визначення логарифмічного декременту затухання
Картину коливань зручно представити не тільки у координатах U, t, (така картина має вид затухаючої синусоїди), але й у координатах Схема включення осцилографа для таких вимірювань коливань у фазовій площині зображена на рис. 6.2. Напруга з конденсатора С подається на вертикальний вхід осцилографа Y. На горизонтальний вхід Х, роль якого виконує вхід осцилографа для синхронізуючого імпульсу, подається напруга з резистора R. Осцилограф в цьому випадку використовується в якості характериографа.
Рис. 6.2. Схема установки для спостереження затухаючих коливань на фазовій площині: 1 - генератор імпульсів, 2 - осцилограф.
Експериментальна установка.
Блок - схема експериментальної установки зображена на рисунку 6.3
Рис.6.3. Блок - схема експериментальної установки. 1 – блок живлення; 2 – звуковий генератор; 3 – перетворювач імпульсів; 4 – осцилограф.
Ємність С, котушка індуктивності L і магазин опорів R утворюють досліджуваний коливальний контур. Коливання в контурі спостерігаються за допомогою осцилографа. Для періодичного збудження коливань в контурі використовується генератор імпульсів. Імпульси заряджають конденсатор С. Після імпульсу в контурі виникають вільні затухаючі коливання. Вхідний опір осцилографа великий (близько 1 МОм), так що його впливом на контур можна знехтувати. Параметри елементів: L = 96,8 мГн, С = 100 нФ, RL = 2 Ом.
Завдання.
1. Перед початком головних вимірювань перевірте справність осцилографа і генератора імпульсів. Для цього подайте сигнал з виходу звукового генератора на осцилограф і визначте при допомозі осцилографа частоту імпульсів. Порівняйте виміряне значення зі значенням частоти на регуляторі генератора. Потім підключить осцилограф до виходу перетворювача імпульсів та визначте тривалість імпульсу, його амплітуду та час між імпульсами. 2. Приступіть до вимірювання. За час вимірювання всі осцилограми занесіть у робочі зошити, вказуючи масштаб по обом осям: а) зберіть схему згідно рисунку 6.3; підбираючи частоту і амплітуду синхронізації, отримайте на екрані осцилографа стійку картину затухаючих коливань; б) перевірте справедливість (6.15). Для цього виміряйте період коливань по картині на осцилографі і обчисліть по формулі (6.15).Значення індуктивності, ємності і активного опору котушки індуктивності вказані на установці; в) дослідіть залежність логарифмічного декременту затухання від величини повного омічного опору контуру (омічний опір котушки індуктивності плюс додатковий опір R, який вводиться у контур) для різних коливальних режимів аж до критичного (не менше чотирьох).
Контрольні питання
1. Що називають власною частотою, добротністю, логарифмічним декрементом затухання коливального контуру? 2. Яка площина називається фазовою площиною коливань? 3. Як визначити логарифмічний декремент затухання контуру по картині коливань у фазовій площині? 4. Отримайте формулу, яка зв’язує період коливань і опір коливального контуру R (при незмінних L і С). Покажіть, що R2 і 1 /T2 залежать один від одного лінійно. Як знайти Rкр по знайденій залежності? 5. Яким чином працює експериментальна установка по вивченню затухаючих коливань в коливальному контурі?
Література
1. Сивухин Д.В. Общий курс физики. т.3 Электричество -М.:Наука, 1983, п.122-124. 2. Калашников С.Г. Электричество. -М.:Наука, 1977, п.207-210. 3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. -М.:Наука, 1983
Лабораторна робота № 7
|
||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1161; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 .
.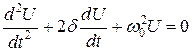 . (6.5)
. (6.5) . (6.8)
. (6.8)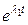 + A2
+ A2  (6.9)
(6.9)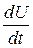 та U.
та U.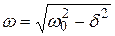 . (6.10)
. (6.10)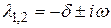 .
.
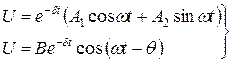 , (6.11)
, (6.11) ,
,  .
. їх амплітудою. Запис рішення у вигляді (6.11) чітко проявляє коливальний характер процесу. Коливання затухають, зменшуючись по амплітуді в e раз за час t = 1 /d. Величина w, яка визначається (6.10), носить назву кругової частоти власних коливань контуру.
їх амплітудою. Запис рішення у вигляді (6.11) чітко проявляє коливальний характер процесу. Коливання затухають, зменшуючись по амплітуді в e раз за час t = 1 /d. Величина w, яка визначається (6.10), носить назву кругової частоти власних коливань контуру.
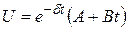 (6.12)
(6.12) (6.13)
(6.13) розряд має аперіодичний, а при
розряд має аперіодичний, а при 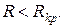 коливальний характер.
коливальний характер.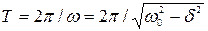 (6.14)
(6.14) і можна користуватися наближеною формулою, яка витікає з (6.14) і (6.4) при малих
і можна користуватися наближеною формулою, яка витікає з (6.14) і (6.4) при малих  :
: . (6.15)
. (6.15) , де n -будь-яке ціле число:
, де n -будь-яке ціле число: .
.

 за час зміни фази на 1 радіан в 2p раз менше, ніж
за час зміни фази на 1 радіан в 2p раз менше, ніж 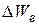 . Покладаючи
. Покладаючи  (слабке затухання) і розкладаючи (1-
(слабке затухання) і розкладаючи (1-  ) в ряд Тейлора, знайдемо:
) в ряд Тейлора, знайдемо: .
. (6.16)
(6.16) і для затухання
і для затухання 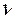 дорівнює логарифму відношень амплітуд двох послідовних відхилень k та k +1 в одну сторону. З (6.11) маємо
дорівнює логарифму відношень амплітуд двох послідовних відхилень k та k +1 в одну сторону. З (6.11) маємо . (6.17)
. (6.17)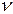 має вигляд:
має вигляд: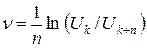 . (6.18)
. (6.18) , U (у фазовій площині). В цих координатах крива незатухаючих коливань (
, U (у фазовій площині). В цих координатах крива незатухаючих коливань ( і
і  ). При наявності затухання (
). При наявності затухання ( ) картина реальних коливань зображується згорнутою спіраллю.
) картина реальних коливань зображується згорнутою спіраллю.