
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимушені коливання у коливальному контуріСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
ПРИЛАДИ: генератор звукової частоти, осцилограф; магазин ємностей; магазин опорів, макет схеми коливального контуру.
В роботі досліджуються вимушені коливання, які виникають у коливальному контурі під дією джерела зовнішньої Е.Р.С., що гармонічно змінюються за часом. Залежність амплітуд встановлених коливань від частоти зовнішньої напруги називається резонансною кривою. Ширина резонансної кривої визначає важливу характеристику контуру - його добротність. Добротність контуру може бути визначена і іншими способами, наприклад по швидкості наростання амплітуд коливань при резонансі. Дослідження резонансних властивостей коливального контуру по вимушеним його коливанням складає мету цієї роботи.
Рис. 7.1. Схема коливального контуру з джерелом зовнішньої Е.Р.С., яке включене послідовно.
Розглянемо процеси які проходять в контурі (рис. 7.1), приєднаному до зовнішнього джерела, Е.Р.С. якого змінюється по гармонічному закону з частотою W e (t) = e0 cosW t.
Визначимо через U напругу на конденсаторі, а через I - струм у контурі. Сума падінь напруг на елементах кола дорівнює зовнішній Е.Р.С.:
Нехай заряд конденсатора дорівнює q, а його ємність - С. Виразимо величину струму I через напругу U:
При підстановці знайденого значення в (7.1) можна отримати:
Це рівняння є кінцевим. Щоб простіше було його дослідити, розділимо обидві частини рівняння на LC і введемо заміну:
де w0 - частота коливального контуру, d - затуханням контуру.
Рівняння (7.4) є неоднорідним (права частина рівняння не дорівнює 0) лінійним диференційним рівнянням другого порядку. Такого типу рівняння описують поведінку широкого класу коливальних систем (електричних, механічних) під впливом зовнішнього синусоїдального впливу (зовнішньої Е.Р.С. або зовнішньої сили). Загальне рішення рівняння (7.4) складається з загального рішення U1 однорідного рівняння:
і будь-якого часткового рішення U 2 неоднорідного рівняння (7.4). Характер загального рішення однорідного рівняння (7.5) залежить від величини затухання
або
Дві форми запису рішення рівняння, (7.6) і (7.7) еквівалентні. Обидві вони мають дві довільні сталі: А 1 і А 2 в першому, В і q -в другому. Ми будемо використовувати другу форму запису. Величина
Тоді дійсна частина цієї функції, тобто
Підставляючи цей вираз у (7.8) отримаємо:
Скорочуючи це рівняння на А =
Замінимо знаменник цього рівняння виразом у показниковій формі:
Модуль останнього виразу дорівнює:
Фаза коливань визначається формулою
Підставимо ці значення в формулу (7.9), знайдемо
і, звідси:
Загальне рішення (7.4) є сумою U 1 і U 2; з допомогою (7.7) і (7.12) отримаємо:
Це рішення має дві довільні сталі: В і О, які визначаються з початкових умов. Формула (7.13) показує, що при дії на контур синусоїдальної Е.Р.С. в ньому виникають коливання двох частот: незатухаючі коливання з частотою зовнішньої Е.Р.С. W (другий член) і затухаючі коливання з власною частотою контуру w (перший член). Амплітуда власних коливань
Якщо частота Uр = e0w0 / 2d.
При
Рівняння (7.14) визначає форму резонансної кривої. Ширина цієї кривої залежить від коефіцієнта
Зміна енергії коливань, яка віднесена до початкової енергії, дорівнює:
За час, коли фаза коливань зміниться на 1 радіан, середня відносна зміна енергії дорівнюватиме
Обернена величина
носить назву добротності контуру. Добротність показує, у скільки разів запасена в контурі енергія перебільшує середню величину енергії, втрачену контуром за час, коли фаза коливань змінюється на 1 радіан. Приведемо другі вирази для добротності контуру:
Підставляючи (7.15) в (7.14), знайдемо:
Ширина резонансної кривої залежить, таким чином, від добротності контуру. При Q>>1 резонансний максимум буде вузьким, так що в області резонансу
В цьому випадку формула (7.17) набуває вигляду:
Зазвичай форму резонансної кривої характеризують шириною
Формули (7.16) вказують на інші способи визначення добротності. Так, добротність контуру дорівнює відношенню напруги на ємності, при резонансі, до напруги на активному опорі. Резонансною кривою називається залежність амплітуди вимушених коливань контуру від частоти зовнішнього джерела Е.Р.С.. Електрична схема установки для дослідження резонансної кривої зображена на рис. 7.2. Експериментальна установка.
Рис. 7.2 Схема для вимірювання резонансної кривої коливального контуру. Резонансний контур складається з індуктивності L, ємності С і резисторів R, R 1. Джерелом зовнішньої Е.Р.С. є звуковий генератор (ЗГ). Вертикальний вхід осцилографа приєднано до резистора R 1, напругу на якому він вимірює. Значення елементів макета схеми таке: L =94.8 мГн, RL =2 Oм, R 1=79 Ом.
Завдання 1. Зібрати схему згідно рис 7.2. 2. Приєднати вертикальний вхід осцилографа до точки Х макета і перевірити працездатність генератора. 3. Дослідити резонансну криву коливального контуру. 3.1. Коливальний контур збирається з ємності С 1 = 1нФ, значення якої встановлюється на магазині ємностей, і R = 10Ом на магазині опору. Змінюючи частоту генератора, отримати резонанс. Обчислити по формулі (7.3.) резонансне значення частоти контуру і зрівняти його з отриманим на досліді. 3.2. Вимірюючи амплітуду коливань на екрані осцилографа при різних значеннях частоти генератора, зняти сімейство залежностей амплітуди встановлених коливань від частоти зовнішньої напруги (резонансні криві) для R = 10, 102, 103, 104 Ом. 3.3. Повторити вимірювання для ємності С 2= 4нФ. 3.4. Накреслити отримані криві для кожного значення ємності на одному графіку, відкладаючи по осі ординат відношення амплітуди коливання, виміряної при зміні значень частоти генератора, до амплітуди, знайденої при резонансному значені частоти. По осі абсцис відкласти величину Дані вимірювання занести у таблицю:
Контрольні питання 1. Вивести формулу (7.19). 2. Знайти часткове рішення рівняння (7.4), не переходячи до комплексних величин. 3. Отримати всі рівності (7.16), які визначають добротність контуру. У чому полягає фізичний зміст добротності? 4. Чому дорівнює власна частота коливального контуру, та його затухання? 5. Розкрити фізичний зміст сталої часу затухання? 6. Яким чином працює експериментальна установка по вивченню вимушених коливань у коливальному контурі?
Література 1. Сивухин Д.В. Общий курс физики. т.3 Электричество. -М.:Наука, 1983, п.124,127. 2. Калашников С.Г. Электричество. -М.:Наука, 1977, п.221,222,-210. 3. Лабораторные занятия по физике. /Под ред. Гольдина Л.Л. -М.:Наука, 1983. Лабораторна робота № 8.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1068; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.13.15 (0.008 с.) |



 . (7.1)
. (7.1)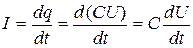
 (7.2)
(7.2) ,
, 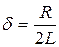 , (7.3)
, (7.3) . (7.4)
. (7.4)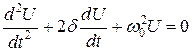 , (7.5)
, (7.5) . Найбільш цікавим є випадок слабкого затухання:
. Найбільш цікавим є випадок слабкого затухання: 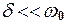 . При цьому загальне рішення рівняння (7.5) має вигляд:
. При цьому загальне рішення рівняння (7.5) має вигляд: , (7.6)
, (7.6) . (7.7)
. (7.7) , що входить в (7.6) та (7.7) є частотою власних коливань контуру;
, що входить в (7.6) та (7.7) є частотою власних коливань контуру;  визначає амплітуду коливань, а
визначає амплітуду коливань, а  їх фазу. Рішення (7.7) описує власні - затухаючі - коливання в контурі. Стала часу затухання
їх фазу. Рішення (7.7) описує власні - затухаючі - коливання в контурі. Стала часу затухання  . Часткове рішення (7.4) простіше за все знайти в комплексній формі, замінивши в його правій частині
. Часткове рішення (7.4) простіше за все знайти в комплексній формі, замінивши в його правій частині  на
на  . Права частина (7.4) пропорційна дійсній частині цього виразу. Нехай рішення нового рівняння є комплексна функція
. Права частина (7.4) пропорційна дійсній частині цього виразу. Нехай рішення нового рівняння є комплексна функція  так, що
так, що . (7.8)
. (7.8) , є рішенням рівняння, у якого в правій частині стоїть
, є рішенням рівняння, у якого в правій частині стоїть  , тобто шукане рішення рівняння (7.4). Будемо шукати часткове рішення (7.8) у вигляді
, тобто шукане рішення рівняння (7.4). Будемо шукати часткове рішення (7.8) у вигляді . (7.9)
. (7.9) .
. і розв¢язуючи його відносно А, прийдемо до рівняння:
і розв¢язуючи його відносно А, прийдемо до рівняння: .
. .
. . (7.10)
. (7.10) . (7.11)
. (7.11)
 . (7.12)
. (7.12) . (7.13)
. (7.13)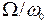 . Дійсно, амплітуда вимушених коливань U0 дорівнює:
. Дійсно, амплітуда вимушених коливань U0 дорівнює: .
. зовнішнього джерела дорівнює власній частоті контуру
зовнішнього джерела дорівнює власній частоті контуру  (резонанс), то амплітуда вимушених коливань досягає свого максимального значення:
(резонанс), то амплітуда вимушених коливань досягає свого максимального значення: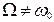 маємо:
маємо: . (7.14)
. (7.14)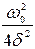 . Вияснимо зміст цього коефіцієнта. Звернемося для цього до вільних коливань контуру, тобто до першого члена рівняння (7.13). Енергія, яка накопичена у контурі в початковий момент часу, пропорційна квадрату амплітуди коливань, тобто
. Вияснимо зміст цього коефіцієнта. Звернемося для цього до вільних коливань контуру, тобто до першого члена рівняння (7.13). Енергія, яка накопичена у контурі в початковий момент часу, пропорційна квадрату амплітуди коливань, тобто  ~ В 2. Ця енергія буде залежати від періоду коливань Т за формулою:
~ В 2. Ця енергія буде залежати від періоду коливань Т за формулою: .
. .
. .
. , (7.15)
, (7.15) . (7.16)
. (7.16) . (7.17)
. (7.17) .
. . (7.18)
. (7.18) , виміряної на рівні
, виміряної на рівні  . Підставляючи у (7.18)
. Підставляючи у (7.18)  , знайдемо, що ширина кривої і добротність контуру пов'язані співвідношенням:
, знайдемо, що ширина кривої і добротність контуру пов'язані співвідношенням: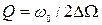 . (7.19)
. (7.19)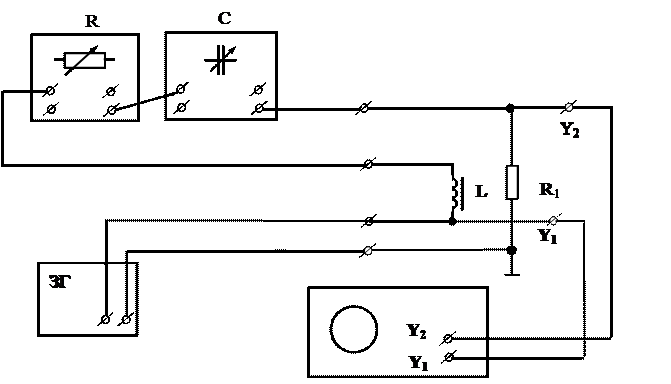
 . Визначити добротність контуру по формулі (7.19).
. Визначити добротність контуру по формулі (7.19).


