
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розділ І. Електромагнітні коливанняСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КОЛИВАННЯ І ХВИЛІ ВСТУП Серед різноманітних фізичних явищ у навколишньому світі особливо поширеними є такі, які періодично або майже періодично повторюються: схід і захід Сонця, хвилювання води на поверхні моря, обертання автомобільних коліс та стрілок годинників, коливання молекул у твердому тілі, змінний електричний струм, електромагнітні хвилі тощо. Биття людського серця, морські припливи й відпливи і навіть рух метро чи автобуса по кільцевому маршруту також є прикладами рухів, які повторюються. Досить різноманітними повторюваними рухами є коливальні рухи. Коливаються гілки дерев на вітрі і маятник в годиннику, поршень у циліндрі двигуна внутрішнього згоряння і земна кора під час землетрусів, струни гітари і корабель на хвилях, крила птаха в польоті і сила струму в колі змінного струму. Коливальні рухи здійснюють атоми в твердих тілах і електрони, які входять до складу атомів. Коливання електричного заряду і сили струму відбуваються в контурах радіоприймачів і телевізорів. За такими самими законами відбувається зміна напруженості електричного поля й індукції магнітного поля в електромагнітній хвилі. Здавалося б, що є спільного між коливаннями маятника і розрядом конденсатора через котушку чи змінним струмом у колі? Однак спільне є. У процесі вивчення цього розділу ви переконаєтеся, що і механічні, і електромагнітні коливання підпорядковуються абсолютно однаковим кількісним законам. Це з'ясовується, якщо цікавитися не тим, що саме коливається (тягарець на пружині, електричний струм у колі чи поверхня води), а тим, я к здійснюються коливання. Однаковим законам підпорядковані також хвильові процеси різної природи. Універсальність законів коливальних процесів дає можливість з єдиної точки зору вивчати різні за фізичною природою коливання, які відбуваються в різноманітних фізичних явищах і технічних пристроях. Саме цим займається фізика коливань — наука, яка виділилася із сучасної фізики і має надзвичайно велике практичне значення. Вона досліджує вібрації машин і механізмів; її висновки лежать в основі електротехніки змінних струмів і радіотехніки. Розділ І. ЕЛЕКТРОМАГНІТНІ КОЛИВАННЯ Негармонічні коливання Вільні коливання тягарця на пружині чи маятника є гармонічними лише тоді, коли немає тертя. Спостереження за вільними коливаннями маятників показують, що їх амплітуда поступово зменшується і через деякий час коливання припиняються. Вільні коливання завжди затухають. Вони вже не є гармонічними і до них незастосовне поняття амплітуди. Однак умовно це поняття зберігають і у випадку затухаючих коливань. Поняття періоду, а також частоти не можна застосовувати до затухаючих коливань, оскільки коливальний рух не повторюється через однакові проміжки часу. Для коливань, які слабо затухають, поняття періоду зберігають. Графік затухаючих коливань показано па малюнку 12. Оскільки сили тертя трохи сповільнюють рух коливальної системи, то період затухаючих коливань поступово спадає. Графік затухаючих коливань неважко дістати, скориставшись маятником з лійкою, заповненою піском. Амплітуда затухаючих коливань і період залежать від характеру сил опору. Практично найбільш цікавим і поширеним в випадок малих коливань, при яких звичайно швидкість тіла невелика і сила опору пропорційна швидкості: Fo= — bv, (5.1) де b — стала, яку називають коефіцієнтом опору; знак мінус показує, що сила опору і швидкість мають протилежні напрями.
Рівняння коливального руху при врахуванні сил опору стане дещо складнішим (воно має включати додаткову силу Fo= — bv): Поділивши всі члени цього рівняння на т і позначивши
Це також лінійне однорідне диференціальне рівняння другого порядку зі сталими коефіцієнтами, які залежать від параметрів системи і коефіцієнта опору Ь. Воно відрізняється від (2.2) наявністю члена з першою похідною від х. Підкреслимо, що коли 6=0, то (5.2) переходить у (2.2). В математиці доводиться, що розв'язком рівняння (5.2) є така функція від t: (5.3)
де є — основа натуральних логарифмів. Графік цієї функції показано на малюнку 13. Пунктирними лініями показано межі, в яких знаходиться зміщення коливної точки х. З рівняння (5.3) видно, що внаслідок спільної дії пружних сил F= —kx і сил опору Fo= — bv система здійснює
коливальний рух, амплітуда якого х,пе (" зменшується з часом за експоненціальним законом, тобто в системі виникають затухаючі коливання. Автоколивання Під час затухаючих коливань енергія системи витрачається на подолання опору середовища. Якщо компенсувати ці втрати енергії, коливання стають незатухаючими. Поповнення енергії системи може здійснюватися за рахунок зовнішньої періодичної сили, причому ця сила має діяти в такт з коливаннями, інакше вона може послабити їх або припинити зовсім. Можна зробити так, щоб коливальна система сама керувала зовнішнім впливом, забезпечуючи узгодженість дії сили із своїм рухом. Така система називається автоколивальною, а здійснювані нею незатухаючі коливання — автоколиваннями. На відміну від вимушених коливань, частота й амплітуда автоколивань визначаються властивостями самої коливальної системи. Автоколкзання відрізняються також від вільних коливань. По-перше, вони з часом не затухають, по-друге, їх амплітуда не залежить від величини початкового короткочасного вшшву, який збуджує коливання. У будь-якій автоколивальній системі можна виділити три основні елементи: 3) коливальну систему; 2) джерело енергії; 3) пристрій із зворотним зь'язком, який регулює надходження енергії із джерела в коливальну систему. Енергія, що надходить із джерела за період, дорівнює енергії, витраченій у коливальній системі за той самий час. Прикладом найпростішої механічної автоколивальної системи може бути годинник з маятником (мал. 14). У ньому коливальною системою є маятник, джерелом енергії — гиря, піднята над землею, або стальна пружина. Основними деталями пристрою, який здійснює зворотний зв'язок, є храпове колесо 1 і анкер 2. Гиря {пружина) обертає храпове колесо. Під час кожного коливання маятника зубець храпового колеса штовхає анкерну вилку, яка розгойдує маятник. У результаті запас енергії, витраченої на подолання сил тертя, поповнюється за рахунок енергії гирі, піднятої над землею, або заведеної пружини. Обертання стрілок годинника здійснюється за допомогою зубчастих коліс від- храпового колеса.
У даному випадку маятник сам «відкриває» і «закриває» доступ енергії із заводного механізму. Під час нормального ходу годинника енергія, яку дістає маятник, дорівнює втраті енергії на тертя за час між двома діями сил. Якщо початкове відхилення маятника перевищує нормальне, то втрати на тертя будуть більшими, ніж надходження енергії із заводного механізму. Коливання затухають доти, поки не встановиться така амплітуда коливань, при якій втрати на тертя компенсуються надходженням енергії із джерела. Отже, амплітуда автоколивань визначається не енергією початкової дії сили, а співвідношенням між втратами і надходженням енергії, тобто властивостями самої коливальної системи. У техніці широко застосовують електромеханічні автоколивальні системи, в яких коливання здійснює механічна система, а надходження енергії регулюється спеціальним електричним пристроєм. Особливо широко автоколивання застосовуються в радіотехніці. Пізніше ви ознайомитеся з будовою автоколивального генератора незатухаючих електромагнітних коливань. Вправа 1 1. Параметри двох коливальних контурів С\ = 1,в«10~10 Ф, Li= 2. Увімкнутий в коливальний контур конденсатор заповнили діелект 3. Коливальний контур складається з котушки індуктивністю Вправа 2 1. Миттєве значення ЕРС синусоїдального струму для фази 60° 2. Амплітуда сили змінного струму Іт= 20 мА, частота v= 103 Гц. 3. ЕРС змінного струму задана рівнянням максимальне значення ЕРС, її значення для фази Генератор змінного струму Розглянутий принцип одержання змінної ЕРС лежить в основі будови більшості технічних індукційних генераторів змінного струму, в яких механічна енергія перетворюється в енергію електричного струму. Схему найпростішого генератора змінного струму дістанемо, якщо виток (див. мал. 21) розріжемо і кінці його з'єднаємо з кінцями зовнішнього кола за допомогою двох ізольованих одне від одного кілець, якими ковзають щітки зовнішнього кола. Збуджувані в послідовно з'єднаних витках ЕРС додаються. Тому для одержання великої ЕРС в промислових генераторах контур, який обертається в магнітному полі, складається з послідовно з'єднаних витків дроту, намотаного яа феромагнітне осердя. ЕРС, збуджувана в такому генераторі, дорівнює:
Існує багато різних типів індукційних генераторів. Однак кожен з них складається з двох основних частин: електромагніту (або постійного магніту) для створення магнітного поля і обмотки, в якій індукується змінна ЕРС (у розглянутій на малюнку 21 схемі генератора — дротяна рамка, що обертається). З рівняння (15.1) видно, що для збільшення ЕРС необхідно збільшувати магнітний потік Ф через витки. Тому магнітну систему генераторів роблять майже замкненою з двох осердь, виготовлених з електротехнічної сталі: зовнішнього кільцеподібного нерухомого і внутрішнього обертового осердя, а повітряний зазор між ними роблять якомога меншим. Генератор має, як правило, дві обмотки, одна розміщується в пазах нерухомого осердя (статора) з внутрішнього його боку, а друга — в пазах обертового осердя (ротора). Одна з обмоток використовується для створення магнітного поля, а друга — є робочою, в ній індукується змінна ЕРС. У розглянутій вище схемі генератора (див. мал. 21) ротором (без залізного осердя) є дротяна рамка. Магнітне поле створюється нерухомим постійним магнітом —
статором. Зрозуміло, що можна зробити й навпаки — обертати магніт, а рамку залишити нерухомою. У великих сучасних генераторах обертається саме електромагніт, який є ротором, у той час як обмотки, в яких збуджується ЕРС, укладені в пазах статора і є нерухомими. На малюнку 22 показана магнітна система сучасного генератора змінного струму. В циліндричній порожнині статора, виготовленого із спеціальної електротехнічної сталі, обертається постійний магніт (в малопотужних генераторах) або електромагніт (в потужних). Обмотка, в якій збуджується ЕРС індукції, укладається у вигляді послідовно з'єднаних рамок у спеціальні пази статора. Магнітна система генератора конструюється так, щоб під час обертання електромагніту індукція В магнітного поля змінювалася за законом утворений вектором В з площиною рамки. Тоді в рамці збуджується ЕРС індукції Доцільність обертання У техніці застосовують змінний п'ятидесятиперіодний струм синусоїдальної форми: струму, який виробляється двополюсним генератором, дорівнює часові одного повного оберту. Тому для одержання змінного струму такої частоти ротор треба обертати з швидкістю 50 обертів за секунду або 3000 обертів за хвилину. Одну пару полюсів мають турбогенератори, ротори яких приводяться в обертання швидкохідною паровою чи газово» турбіною. 1 1. Який принцип роботи генераторів змінного струму? 2. Як збільшують ЕРС індукції в обмотці статора? 3. Чому в потужних генераторах ротором в електромагніт, а ЕРС збуджується в нерухомих обмотках? 4. Пояснити виникнення ЕРС індукції в нерухомих обмотках статора. Періодичних процесів У реальних системах коливання можуть розглядатися як гармонічні лише з певним ступенем наближення; вони носять більш складний характер. Спостерігаються коливання настільки складні за формою, що описати кожне з них одним гармонічним законом не можна. Наприклад, не підпорядковані гармонічному закону сейсмічні коливання земної кори під час землетрусів. Жоден коливальний процес у природі чи в техніці не триває нескінченно довго, а має початок і кінець у часі. Оскільки коливальний процес обмежений у часі, він не є гармонічним. Будь-яке реальне коливання відбувається з поступовою витратою енергії руху на роботу проти сил тертя і на випромінювання, а тому не є гармонічним. Спостерігаються в природі коливальні процеси, які тривають дуже довго. Прикладом коливань такого роду можуть бути періодичні зміни напруги між різними ділянками людського тіла, які виникають в результаті роботи серця. Графік залежності «вироблюваної» серцевими м'язами напруги від часу називається електрокардіограмою (мал. 41). Вона дуже мало схожа на синусоїду (чи косинусоїду), тобто коливання біострумів є негармоніч-ними. Із складними негармонічними коливаннями мають справу в радіотехніці. Часто такі коливання є результатом додавання кількох гармонічних коливань з різними частотами, амплітудами, фазами тощо. Природно поставити запитання: якщо в результаті додавання простих гармонічних коливань виникають складні, різноманітні за формою результуючі коливання, то чи не можна подати складні коливання як суму простих гармонічних? Наприклад, на малюнку 42 зображено жир-
ною лінією коливання явно не гармонічне. Але його можна дістати, додаючи гармонічні коливання з частотами вання можна подати у вигляді суми * основного тону», який відповідає частоті Виявляється, розкладання складного коливання на ряд простих гармонічних коливань з частотами, кратними частоті складного коливання, яку називають основною частотою, можливе завжди. Причому, для кожного конкретного виду коливання розкладання можна здійснити єдиним способом. Закони такого розкладання сформулював у минулому столітті французький вчений Фур'є у вигляді теореми, яка відіграє величезну роль в сучасній науці й техніці Він довів, що майже будь-яка періодична функція з періодом 7і, задана на інтервалі від Цей ряд називають рядом Фур'є. Перша складова в ньому ною, гармонічною складовою розкладання з періодом Т, що дорівнює періоду функції Якби для аналізу періодичної функції f(t) однаково важливими були всі члени нескінченного тригонометричного ряду Фур'є (23.1), то гармонічний аналіз не мав би практичного значення, оскільки за його допомогою не можна було б здійснити жодних обчислень. Однак в дійсності амплітуда гармонік ряду Фур'є зі збільшенням номера п зменшується. Тому для практичної мети виявляється можливим використовувати замість нескінченного ряду тригонометричних функцій їх скінченне число. Кількість членів ряду Фур'є, які необхідно використати в розрахунках, визначається виглядом функції Результат гармонічного аналізу часто подають у вигляді так званого спектра складного коливання. Для цього на горизонтальній осі відкладають частоти складових гармонічних коливань, а вертикальними рисками (ординатами) позначають відповідні їм амплітуди. На спектрі не можна відобразити фази коливань, але нерідко буває достатньо знати частоти і амплітуди. Для прикладу розглянемо результат розкладання в спектр негармонічної періодичної функції, графік якої показано на малюнку 43. Періодичний коливальний процес, що його описує ця функція, можна дістати, наприклад, в електричному колі, яке складається з джерела струму з напругою U на вихідних клемах, вимикача К і резистора R (мал. 44). Якщо вимикач К замкнути і через інтервал часу т розімкнути, а потім через час Т після першого замикання знову замкнути на час т і таким чином повторювати процес вмикання і вимикання, то графік залежності напруги на резисторі R від часу матиме вигляд, показаний на малюнку 43. Амплітудний спектр гармонічних складових періодичної послідовності прямокутних імпульсів до 10-ї гармоніки показано на малюнку 45.
Гармонічний спектр складного коливання, який містить лише невелику кількість простих коливань і графік якого складається з окремих ординат, називається лінійчастим. Якщо спектр містить прості коливання практично всіх частот, він називається суцільним і графік його будується у вигляді кривої, яка обгинає верхівки ординат. Розкладання на прості гармонічні коливання виявляється можливим не лише для періодичних, а й для типово неперіодичних процесів (окремий імпульс, затухаючі коливання тощо). Неперіодичний процес можна подати як суму нескінченно великої кількості гармонічних коливань з амплітудами, які змінюються безперервно з усіма частотами. Розкладання складного коливання на прості (гармонічні) або, інакше кажучи, знаходження його гармонічного спектра є основним прийомом аналізу складного коливання. В імпульсній техніці гармонічний аналіз дає можливість виконувати розрахунки електричних кіл під час проходження ними електричних сигналів складної форми, застосовуючи прості правила розрахунку електричних кіл для його гармонічних складових. Часто гармонічний аналіз складних коливань здійснюють за допомогою спеціальних спектральних приладів — гармонічних аналізаторів. ? 1. У чому полягав суть методу гармонічного аналізу періодичних функцій? 2. Що такс спектр складного коливання і який вигляд має лінійчастий спектр негармонійного коливання? КОРОТКІ ПІДСУМКИ Й ВИСНОВКИ 1. Періодичні зміни заряду, сили струму й напруги
2. Основне рівняння вільних електромагнітних коли
3. Електромагнітні коливання високої частоти можна 4. Важливим прикладом вимушених електромагнітних 5. визначається рівністю 6. Діючі значення сили струму і напруги змінного 7. На конденсаторі коливання Він є опором реактивним, тобто в колі з ємністю відбуваються періодичні перетворення енергії струму і не відбувається її поглинання. 8. На котушці індуктивності коливання напруги випе
9. Закон Ома для кола змінного струму з послідовно
10. Потужність змінного струму на ділянці кола визна 11. коливального контуру сили струму під час резонансу різко зростають напруги на конденсаторі і котушці індуктивності. Під час резонансу зсув фаз між струмом і напругою стає рівним нулю. Генератор трифазного струму Поряд з простим синусоїдальним змінним струмом у техніці для одержання, передавання й розподілу електроенергії широко використовується трифазний струм. Уявимо собі прямокутну дротяну рамку з кількома витками, яка рівномірно обертається в однорідному магнітному полі. ЕРС індукції в цій рамці змінюється за синусоїдальним законом. Якщо навколо спільної осі обертається не одна, а три однакові рамки, площини яких повернуті одна відносно одної на 120° (мал. 51), то ЕРС в них будуть зміщені за фазою на
(26.1) Обмотку кожної з цих рамок можна замкнути на своє навантаження (мал. 52), і дістати три синусоїдальні змінні
струми, між якими буде стала різниця фаз. Такі три узгоджені змінні струми називають трифазним струмом. Трифазна система змінного струму має, як побачимо далі, ряд переваг перед однофазною. Трифазну систему змінного струму принципово можна дістати від трьох однакових генераторів змінного однофазного струму, ротори яких, знаходячись в одному і тому ж положенні, жорстко зв'язані між собою і не змінюють свого відносного положення під час обертання. Статорні обмотки генераторів повернуті одна відносно одної на 120° у бік обертання ротора, як це показано на малюнку 53 (кінці їх позначені буквами 77 і К). У цих умовах цілком очевидно, що ЕРС другого генератора є? запізнюватиметься у своїх змінах відносно ЕРС першого генератора е\ на 120°,
тобто максимальне значення ЕРС того самого напряму в другому генераторі настане після того, коли всі ротори генераторів повернуться на 120°. ЕРС третього генератора ез також буде запізнюватися відносно ЕРС другого генератора на 120°. Але такий спосіб одержання трифазного струму технічно складний і економічно невигідний. Набагато простіше всі три статорні обмотки об'єднати в одному корпусі статора (мал. 54). Такий генератор називають генератором трифазного струму. Якщо генератор двополюсний, як на малюнку 54, то обмотки фази зсунуті одна відносно одної на одну третину кола статора. Під час обертання ротора його постійне магнітне поле перетинає провідники обмоток не одночасно. ЕРС обмотки коли повз неї проходить середина полюса ротора. ЕРС в наступній обмотці ротор повернеться на повороту на в обмотці
і від ЕРС обмотки будови генератора максимальні значення цих ЕРС одна-
кові. Конструкція генератора повинна забезпечувати їх синусоїдальність. Рівняння миттєвих значень ЕРС виражаються формулами (26.1). Криві миттєвих значень ЕРС показані на малюнку 55; на малюнку 56 подана векторна діаграма для їх діючих значень
Сума цих векторів утворює замкнутий трикутник: що легко перевірити, підставивши вирази цих значень для синусоїдальних функцій часу. Від послідовності фаз системи залежить, як ми в цьому переконаємося далі, напрям обертання трифазних двигунів, тому в трифазних установках вона перевіряється спеціальними покажчиками послідовності фаз і позначається забарвленням шин на розподільних пристроях; у нашій країні прийняті такі кольори: фаза А — жовтий; фаза В — зелений і фаза С — червоний; незаземлена ней-траль — білий, заземлена нейтраль — чорний. Затискачі обмоток генератора розрізняють так: початки А, В, С; кінці АГ, У, Z. Лінійні і фазні напруги Для чого потрібна трифазна система струмів? Які її переваги? Щоб відповісти на ці запитання, спочатку розглянемо, як вмикається навантаження до трифазного генератора. Обмотки фаз генератора можна було б з'єднати з трьома споживачами електроенергії шістьма проводами
(мал. 57, а) і дістати таким шляхом три незалежні фазні кола. Практично подібне з'єднання застосовується рідко, але за допомогою такої схеми можна легко зрозуміти умови, які виникають при об'єднанні кіл у трифазну систему. Оскільки для явищ в електричних колах важлива лише різниця потенціалів, то можна об'єднати в один провід по одному проводу з кожного кола. В результаті з'єднання генератора із споживачем здійснюється за допомогою чотирьох, а не шести проводів. Таке з'єднання називають з'єднанням зіркою (мал. 57, б). Якщо об'єднати по одному проводу з кожного кола на малюнку 57, а попарно, то одержимо схему з'єднання генератора із споживачем трьома проводами, яку називають з'єднанням трикутником (мал. 58). Для з'єднання зіркою затискачі X, У, Z («кінці» обмоток фаз генераторів) об'єднуються в одну спільну точку N. Відповідно в точці п об'єднуються і три кінці фазних кіл споживача енергії (мал. 59). Між нейтральними точками генератора і споживача прокладено спільний нейтральний
(27.1) Додаючи ці гармонічні коливання за допомогою векторних діаграм (мал. 60), дістанемо струму в нейтральному проводі дорівнює нулю. Тому для симетричного трифазного навантаження (коли сила струму в усіх фазах однакова і рівні зсуви фаз між фазними напругами й струмами) нейтральний провід не потрібний. Зокрема, він не використовується при вмиканні трифазних двигунів. Але коли навантаження несиметричне, як наприклад, в освітлювальній мережі в будинках (мал. 61), то в нульовому проводі виникає невеликий «компенсаційний» струм.
При з'єднанні обмоток фаз генератора трикутником (мал. 62) початок однієї обмотки фази з'єднують з кінцем попередньої (А з Z, В з X і С з У). Додатні напрями ЕРС при такому з'єднанні напрямлені всередині трикутника обмоток фаз однаково; отже, всередині цього трикутника діє алгебраїчна сума миттєвих значень фазних ЕРС. Але В колах трифазного струму напруги між кінцями кожної обмотки генератора називають фазними напругами, а струми в цих обмотках — фазними струмами. Так само називають напруги і струми в навантаженнях. Напруги між проводами 1,2, 3 на малюнку 57, б і між будь-якою парою проводів на малюнку 58, називаються лінійними напругами, а струми в цих проводах — лінійними струмами. Легко бачити, що при з'єднанні зіркою фазні струми збігаються з лінійними струмами (оскільки всі частини
фазного кола і лінійні проводи з'єднані послідовно); а фазні і лінійні напруги відрізняються. При з'єднанні трикутником, навпаки, фазні напруги є одночасно лінійними, а фазні і лінійні струми відрізняються. Числові співвідношення між лінійними і фазними напругами в симетричній системі легко визначити на основі векторної діаграми. Побудуємо векторну діаграму напруг для з'єднання зіркою. Припустимо, що генератор розімкнутий. Тоді фазні напруги збігаються з відповідними ЕРС, і оскільки останні зсунуті за фазою на 120° і 240°, то діаграма фазних напруг трифазних двигунів, а фазна— на освітлю- вальні прилади. У випадку чисто освітлювального навантаження при з'єднанні зіркою споживачі вмикаються між лінійними проводами і нейтральним проводом. Коли освітлювальне навантаження несиметричне, необхідний нейтральний провід (див. мал. 61). При відсутності нейтрального проводу залежно від співвідношення опорів фаз споживача одна фазна напруга може бути нижчою від необхідної, а друга занадто великою. З цієї причини в нейтральному проводі магістралі забороняється встановлювати запобіжники або вимикачі. Так само просто будується векторна діаграма фазних струмів при з'єднанні трикутником. Коли навантаження симетричне, за допомогою векторної діаграми можна переконатися, що амплітуди лінійних струмів будуть в більші, ніж амплітуди фазних струмів. Нагадаємо (це легко бачити з малюнка 58), що при з'єднанні трикутником лінійна і фазна напруги однакові вище результати можна дістати й аналітично, не ко
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 793; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.217.237.68 (0.012 с.) |


 одержимо рівняння руху в такому вигляді:
одержимо рівняння руху в такому вигляді: (5.2)
(5.2)


 . Знайти
. Знайти , частоту й період струму.
, частоту й період струму. (15.1)
(15.1)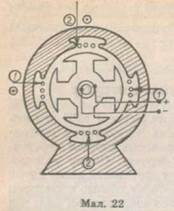
 — кут,
— кут, електромагніту, а не робочої обмотки генератора, пояснюється тим, що сила індукованого генератором струму в багато разів перевищує силу струму в електромагніті, а струм великої потужності конструктивно дуже складно відводити від обертового якоря. Слабкий струм до обертового електромагніту (ротора) підводиться за допомогою ковзного контакту. Для цього до кінців обмоток ротора приєднують контактні кільця, а нерухомі пластини — щітки, притиснуті до кілець, з'єднують обмотки ротора з зовнішнім колом. Обмотку статора,в якій індукується потужний струм, з'єднують нерухомими шинами з лінією, якою електроенергія передається до споживачів.
електромагніту, а не робочої обмотки генератора, пояснюється тим, що сила індукованого генератором струму в багато разів перевищує силу струму в електромагніті, а струм великої потужності конструктивно дуже складно відводити від обертового якоря. Слабкий струм до обертового електромагніту (ротора) підводиться за допомогою ковзного контакту. Для цього до кінців обмоток ротора приєднують контактні кільця, а нерухомі пластини — щітки, притиснуті до кілець, з'єднують обмотки ротора з зовнішнім колом. Обмотку статора,в якій індукується потужний струм, з'єднують нерухомими шинами з лінією, якою електроенергія передається до споживачів. Період змінного
Період змінного

 і
і  , причому
, причому  . Таким чином, дане складне коли-
. Таким чином, дане складне коли- , і «обертонам, який відповідає частоті
, і «обертонам, який відповідає частоті 
 , може бути
, може бути  розкладена в нескінченний тригонометричний ряд гармонічних функцій з певними амплітудами і фазами, частоти яких кратні основній частоті і сума яких дав функцію
розкладена в нескінченний тригонометричний ряд гармонічних функцій з певними амплітудами і фазами, частоти яких кратні основній частоті і сума яких дав функцію 
 :
: — стала складова функції
— стала складова функції  , незалежна від часу. Друга складова
, незалежна від часу. Друга складова  в першою, або основ-
в першою, або основ- . Третю складову називають другою гармонікою. її період вдвічі менший, ніж період функції
. Третю складову називають другою гармонікою. її період вдвічі менший, ніж період функції  . Період третьої гармоніки втричі менший, ніж Т і т. д.
. Період третьої гармоніки втричі менший, ніж Т і т. д. і заданою точністю обчислень.
і заданою точністю обчислень.

 (формула Томсона).
(формула Томсона). . Якщо опір контуру R
. Якщо опір контуру R
 . Сила
. Сила
 На активному опорі електромагнітна енергія генератора повністю перетворюється в інші види енергії. Коливання сили струму на цьому опорі збігаються за фазою з коливаннями напруги, а амплітуда сили струму
На активному опорі електромагнітна енергія генератора повністю перетворюється в інші види енергії. Коливання сили струму на цьому опорі збігаються за фазою з коливаннями напруги, а амплітуда сили струму
 сили струму випере
сили струму випере . Величину
. Величину 
 . Величину
. Величину 
 називають індуктивним опором. У випадку індуктивного опору також не відбувається споживання енергії генератора.
називають індуктивним опором. У випадку індуктивного опору також не відбувається споживання енергії генератора. називають повним опором кола.
називають повним опором кола. між напругою і струмом:
між напругою і струмом: 
 Різке зростання амплітуди вимушених коливань сили струму в коливальному контурі з малим активним опором — резонанс — відбувається тоді, коли збігаються частоти зовнішньої змінної напруги з власною частотою
Різке зростання амплітуди вимушених коливань сили струму в коливальному контурі з малим активним опором — резонанс — відбувається тоді, коли збігаються частоти зовнішньої змінної напруги з власною частотою . Одночасно із зростанням
. Одночасно із зростанням :
:



 досягає свого максимального значення,
досягає свого максимального значення, досягає максимуму пізніше, коли
досягає максимуму пізніше, коли оберту. В двополюсному генераторі
оберту. В двополюсному генераторі оберту відповідав
оберту відповідав  періоду індукованої ЕРС. Отже, ЕРС в обмотці
періоду індукованої ЕРС. Отже, ЕРС в обмотці  відстає за фазою від ЕРС
відстає за фазою від ЕРС наперіоду.
наперіоду.  В свою чергу, ЕРС в обмотці
В свою чергу, ЕРС в обмотці відстає за фазою від ЕРС обмотки
відстає за фазою від ЕРС обмотки  наперіоду
наперіоду 
 наперіоду.
наперіоду.  При такій симетрії
При такій симетрії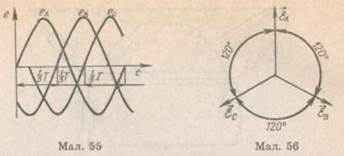

 — це трифазна симетрична система ЕРС. Алгебраїчна сума миттєвих значень ЕРС
— це трифазна симетрична система ЕРС. Алгебраїчна сума миттєвих значень ЕРС  ,
,

 провід (або нульовий) трифазної системи, утворений об'єднанням трьох зворотних проводів. Якщо у всі три фазні кола увімкнути однакові навантаження, то амплітуда сили струму у всіх трьох колах буде одна й та сама:
провід (або нульовий) трифазної системи, утворений об'єднанням трьох зворотних проводів. Якщо у всі три фазні кола увімкнути однакові навантаження, то амплітуда сили струму у всіх трьох колах буде одна й та сама:
 . Тобто сила
. Тобто сила



 , тому компенсуючий струм в обмотках генератора не виникає. Отже, певною перевагою з'єднання фаз трикутником є та, що при несиметричному навантаженні немає необхідності використовувати четвертий провід. На малюнку 63 показана схема освітлювальної мережі житлового будинку при з'єднанні фаз споживачів трикутником.
, тому компенсуючий струм в обмотках генератора не виникає. Отже, певною перевагою з'єднання фаз трикутником є та, що при несиметричному навантаженні немає необхідності використовувати четвертий провід. На малюнку 63 показана схема освітлювальної мережі житлового будинку при з'єднанні фаз споживачів трикутником.

 має вигляд, показаний на малюнку 64. Як видно з малюнка 57, б, миттєве значення лінійної напруги між, наприклад, проводами 1 і 2 дорівнює різниці миттєвих значень відповідних фазних напруг. Тому вектор
має вигляд, показаний на малюнку 64. Як видно з малюнка 57, б, миттєве значення лінійної напруги між, наприклад, проводами 1 і 2 дорівнює різниці миттєвих значень відповідних фазних напруг. Тому вектор  дорівнює різниці векторів
дорівнює різниці векторів  , які зображають фазні напруги в першій і другій обмотках (див. мал. 64). Зрозуміло, що вектор
, які зображають фазні напруги в першій і другій обмотках (див. мал. 64). Зрозуміло, що вектор  можна перенести паралельно самому собі так, щоб його початок збігся із загальним центром обертання векторів. З малюнка видно, що амплітуда лінійної напруги при з'єднанні зіркою в
можна перенести паралельно самому собі так, щоб його початок збігся із загальним центром обертання векторів. З малюнка видно, що амплітуда лінійної напруги при з'єднанні зіркою в  разів більша, ніж амплітуда фазної. Якщо, наприклад, фазна напруга в мережі 220 В, то лінійна напруга в ній 380 В. При^змішаному освітлювальному і силовому навантаженні лінійна напруга 380 В подається на затискачі
разів більша, ніж амплітуда фазної. Якщо, наприклад, фазна напруга в мережі 220 В, то лінійна напруга в ній 380 В. При^змішаному освітлювальному і силовому навантаженні лінійна напруга 380 В подається на затискачі
 разів
разів . Всі приведені
. Всі приведені


