
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимушені коливання системи ротор-аксіально рухома втулка торцевого сальникового ущільненняСодержание книги
Поиск на нашем сайте
Динамічні моделі А и В являють собою пов'язані двомасові системи, які вчиняють малі осьові коливання щодо положення статичної рівноваги. При цьому поточні значення змінних можна представити у вигляді
На підставі 2-го закону Ньютона для моделі А:
Виключивши рівняння рівноваги та опускаючи для скорочення знак
де
Введемо оператор диференціювання по часу
(2.28)
де
(2.29)
диференційні оператори Подібним шляхом отримаємо систему рівнянь спільних коливань моделі В:
(2.30)
Модель В відрізняється від моделі А власною частотою парціальної системи вала і перехресним оператором:
Тут розглядаються коливання сальникової втулки і ротора, обумовлені малими гармонійними коливаннями ущільнюваного тиску
Користуючись формулами Крамера, запишемо рішення систем рівнянь (2,28) і (2,30): для схеми А:
для схеми В: (2.34)
де власні оператори систем
Для гармонійних коливань оператор диференціювання для схеми А
Остальні оператори мають вигляд: для обох схем
для схеми А
для схеми В
Підставивши (17) і (18) в формули (15), отримаємо
Як амплітудно частотну характеристику приймемо безрозмірну величину, яка пропорційна модулю частотної передавальної функції
Фазова частотна характеристика – аргумент передаточної функції:
Для подальших розрахунків введемо безрозмірну частоту і показники загасання:
(2.40)
Амплітудна характеристика вала
а після переходу до безрозмірного вигляду
Подібним чином знайдемо амплітудні частотні характеристики втулки і ротора схеми В:
З урахуванням (2.36) та (2.37), отримаємо
Для порівняння наведемо амплітудні характеристики відповідних консервативних систем, вважаючи
(2.44)
З перших формул (2.43) і (2.44) видно, що на частоті обертання Формули (2.40) - (2.42) дають можливість оцінити розмірну амплітуду для будь-якої частоти обертання по заданій амплітуді гармонійного впливу
Нормальна робота ущільнення характеризується наявністю постійного контакту між торцевими поверхнями сальникової набивки і опорного диска. Однак, при вимушених осьових коливаннях диска змінюється деформація набивки і контактний тиск, а при досить великих амплітудах можливо періодичне розкриття торцевого стику. Розкриття стику супроводжується різким збільшенням протікання, тому його потрібно уникати. Для моделі А величина стиснення набивки в рівноважному стані
Для моделі В
Останні нерівності можна використовувати для вибору відносної жорсткості Чисельний розрахунок
10. Насос двостороннього входу (типу Д) тиск нагнітання 20. Консольний конденсатний насос, тиск нагнітання Більшість подібних насосів за параметрами займає проміжне положення, тому розрахунок таких крайніх варіантів дозволяє судити про динаміку ущільнень з проміжними параметрами. На малюнках наведені амплітудно-частотні характеристики для консервативних систем (ϛ=0).

Рисунок 2.10 – АЧХ втулки і ротора схеми А (а) і схеми B (б) в безрозмірному вигляді
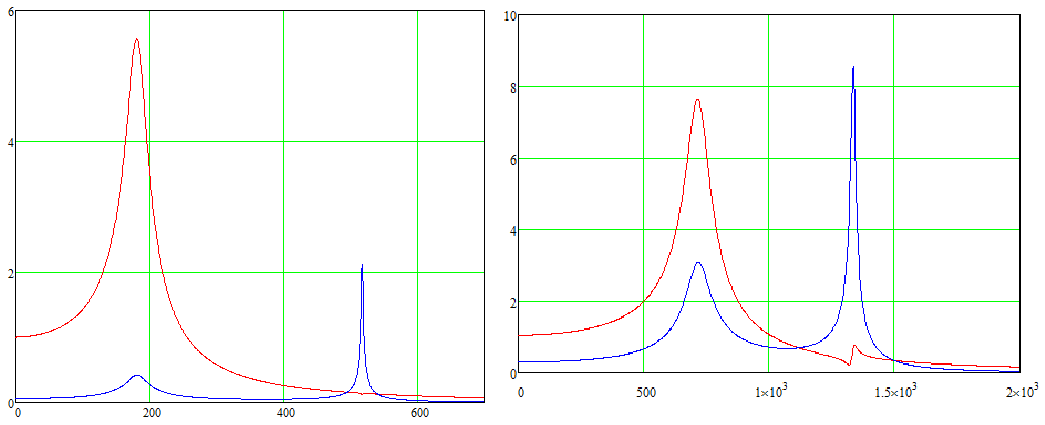
Рисунок 2.11 – АЧХ втулки і ротора схеми А (а) і схеми B (б) в розмірному вигляді

Рисунок 2.12 – АЧХ втулки і ротора схеми А (а) і схеми B (б) в розмірному вигляді при зменшенні коефіцієнту жорсткості сальникової набивки
Висновки 1. Ротор і аксіально-рухома втулка торцевого сальника утворюють слабо пов’язану двомасову систему з пружньо-демпферними зв’язками. Статичний розрахунок системи дозволяє підібрати початкове зміщення натискної втулки 2. В якості першого наближення в диференціальних рівняннях сумісних коливань можна знехтувати перехресними зв’язками, враховуючи, що 3. Власна частота осьових коливань втулки 4. Власна частота ротора як другої парціальної системи в схемі А з обертовою втулкою не залежить від жорсткості набивки, на відміну від схеми В, в якій коливання ротора безпосередньо впливають на набивку. 5. Для ущільнення з аксіально-рухомою втулкою, що обертається кінематичне збудження передається через порівняно податливі пружні елементи, тому амплітуда резонансних коливань на порядок менша, ніж для ущільнення з втулкою, що не обертається. 6. На АЧХ коливань втулки видимі антирезонанси на другій парціальній частоті.
ВИСНОВКИ 1. Проведено аналіз існуючих конструкцій торцевих механічних, сальникових та торцевих сальникових ущільнень. Перераховано їх основні переваги та недоліки. 2. Виконаний аналіз осьових коливань реального торцевого сальникового ущільнення на прикладі двох різних по розмірам типових конструкцій (насос двостороннього входу (типу Д) і консольний конденсатний насос), та їх статичний розрахунок, що дає змогу визначити необхідні параметри для початкового підтиснення. Попередня деформація пружних елементів та набивки, при яких торцевий стик не буде розкриватися складає не менше 6,2 мм для моделі А та не менше 5,5 мм для другої моделі. Оскільки в розглянутих прикладах резонансні режими знаходяться далеко від номінальних, можна рекомендувати На підставі побудованих графіків амплітудно-частотних характеристик для торцевого сальникового ущільнення та системи ротор – аксіально-рухома втулка можна сказати, що робота ущільнення на резонансному режимі малоймовірна через те, що частоти, на яких виникає резонанс в декілька разів перевищують робочу частоту. 3. Проведений аналіз залежності амплітудно-частотної характеристики від величини коефіцієнтів жорсткості пружних елементів та сальникової набивки. При початкових величинах коефіцієнтів жорсткості пружних елементів резонанс наступав на частоті обертання, що вдвічі перевищувала робочу. При підвищенні коефіцієнтів жорсткості резонансна частота перевищувала робочу майже втричі. Пониження коефіцієнту пружності сальникової набивки призвело до наближення резонансної частоти до робочої з різницею в 40 об/сек між величинами.
ПЕРЕЛІК ПОСИЛАНЬ 1. Голубев А. И. Торцовые уплотнения вращающихся валов / А. И. Голубев. – 2-е изд., перераб. и доп. – М.: Машиностроение, 1974. – 216 с. 2. Гудков С. Н. Торцовое сальниковое уплотнение с гидродинамической разгрузкой пары трения: диссертация на соискание научной степени канд. технических наук / С. Н. Гудков; Науч. рук. А.В. Загорулько. — Сумы: СумГУ, 2015. — 154 с. — СумГУ. 3 Марцинковський, В. А. Гермомеханіка. Розділ "Теорія і конструкція механічних торцевих ущільнень": конспект лекцій для студ. спец. 8.080303 "Динаміка і міцність" денної форми навчання / В. А. Марцинковський, С. М. Гудков, С. О. Міщенко. — Суми: СумДУ, 2009. — 68 с. — 6-02.4. 4. Максимов В. А. Бесконтактные уплотенения роторов центробежных 5..Kundera Czesław Problemy uszczelnień zespołow wirujących / Czesław Kundera. – Kielce: Politechnika Świętokrzyska, 2013. – 286 s.6. 6. Макаров Г. В. Уплотнительные устройства / Г. В. Макаров. – 2-е изд., перераб. и доп. – Л.: Машиностроение, 1973. – 232 с. 7 Сайт [Электронный ресурс]. – Режим доступа: http://chem21.info/info/1024245/ 8. Марцинковский В.А. Динамические характеристики торцового уплотнения с мягкой набивкой / Марцинковский В.А., Гудков С.Н., Ч. Кундера // Компрессорное и энергетическое машиностроение. – 2015. 9. Марцинковский В.А. Анносы атомных электростанций / В.А. Марцинковский, П.Н. Ворона. – М.: Энергоатомиздат, 1987. – 256 с. 10.Загорулько А.В. Экспериментальные исследования новых конструкций торцовых сальниковых уплотнений с гидродинамической разгрузкой пары трения / А.В. Загорулько, С.М. Гудков // Вісник СхідноукраїнськогоНаціонального університету імені Володимира Даля. – 2007. – №3. – С. 91-97 11.Марцинковский В.А. Осевые колебания системы ротор – торцевое сальниковое уплотнение / Марцинковский В.А., Гудков С.Н., Ч. Кундера // Компрессорное и энергетическое машиностроение. – 2015. – №4(42). – С. 5 – 10. 12. Марцинковский В. А. Динамика роторов центробежных машин: монография / В. А. Марцинковский. — Сумы: СумГУ, 2012. — 562 с. 13. Сайт [Электронный ресурс]. – Режим доступа: Сравнительная характеристика материалов сальников / http://pa-rti.ru/material. 14. Сайт [Электронный ресурс]. – Режим доступа: http://www.salnik.ru/company/technologies/kakie-salniki-lutsche-tpfe-vs-viton.html 15.. Марцинковский В. А. Вибрации роторов центробежных машин. Кн.1:Гидродинамика дросселирующих каналов / В. А. Марцинковский. – в 2-х кн. – Сумы: СумГУ, 2002. – 337 с. 16 Сайт [Электронный ресурс]. – Режим доступа: http://www.stroitelstvo-new.ru/nasosy/salnikovye-uplotneniya.shtml 17 Голубев Г.А., Контактные уплотнения вращающихся валов / Голубев Г.А., Кукин Г.М., Лазарев Г.Е.// Машиностроение. – 1976. – 264 с.
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 200; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.34.211 (0.01 с.) |

 ,
, 
 ,
, 


 , отримаємо пов’язану систему
, отримаємо пов’язану систему (2.26)
(2.26) . (2.27)
. (2.27) та представимо рівняння (2,26) в операторному вигляді:
та представимо рівняння (2,26) в операторному вигляді: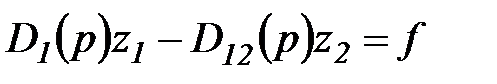

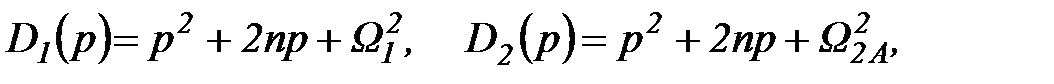

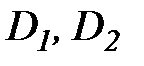 - власні оператори ізольованих (парціальних) систем,
- власні оператори ізольованих (парціальних) систем,  - перехресний оператор, який визначає пружно-демпферний зв'язок між коливаннями мас
- перехресний оператор, який визначає пружно-демпферний зв'язок між коливаннями мас  .[11]
.[11] ,
, .
. . (2.31)
. (2.31) щодо його сталого значення. Останнє, як правило, є тиском нагнітання розглянутого насоса або компресора. При цьому збурення і реакція на нього системи мають вигляд:
щодо його сталого значення. Останнє, як правило, є тиском нагнітання розглянутого насоса або компресора. При цьому збурення і реакція на нього системи мають вигляд: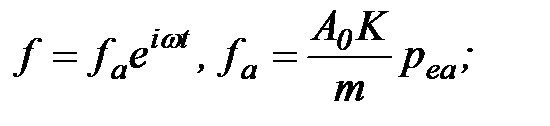 (2.32)
(2.32) ; (2.33)
; (2.33) - амплітуди і фази вимушених коливань втулки і ротора відповідно, знаки варіацій при
- амплітуди і фази вимушених коливань втулки і ротора відповідно, знаки варіацій при  опущені.[11]
опущені.[11]

 . (2.35)
. (2.35)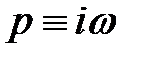 . Введемо цю заміну і розділимо дійсні і уявні частини операторів. Для цього помножимо чисельник і знаменник на спряжене знаменнику комплексне число. В результаті отримаємо для власного оператора систем
. Введемо цю заміну і розділимо дійсні і уявні частини операторів. Для цього помножимо чисельник і знаменник на спряжене знаменнику комплексне число. В результаті отримаємо для власного оператора систем  :
:
 ;
для схеми В
;
для схеми В


 ;
;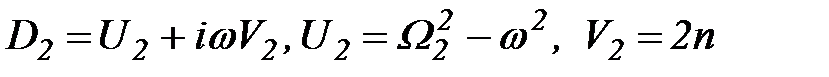 ,
, . (2.37)
. (2.37) .
. .
. =
= 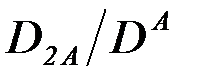 :
: . (2.38)
. (2.38) . (2.39)
. (2.39) . При цьому формули (2.38) і (2.39) запишемо в розгорнутому вигляді:
. При цьому формули (2.38) і (2.39) запишемо в розгорнутому вигляді: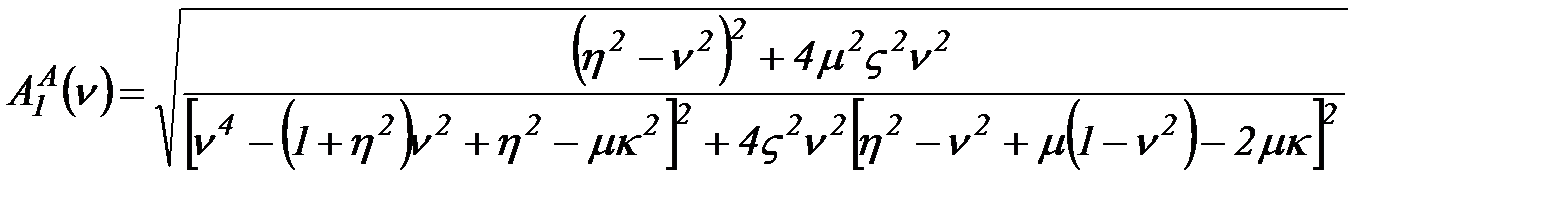
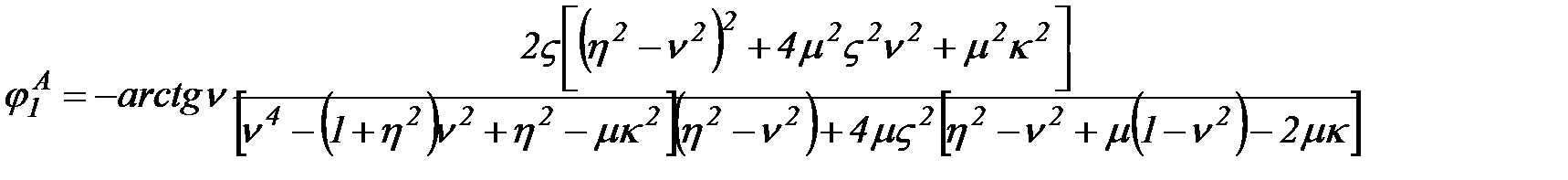
 ,
, . (2.41)
. (2.41) .
. (2.42)
(2.42) .
. і з огляду на відмінність других власних частот парціальних систем
і з огляду на відмінність других власних частот парціальних систем  :
: ,
,  (2.43)
(2.43) ,
, .
.
 , тобто на частоті обертання, що дорівнює власній частоті другої парціальної системи, амплітуда вимушених коливань втулки дорівнює нулю. У теорії коливань це явище отримало назву антирезонанса, а схеми, подібні наведеним на рис.3, близькі до схем динамічних гасителів коливань маси т. У дисипативних системах явище антирезонанса кілька згладжується демпфірувальними силами.[11]
, тобто на частоті обертання, що дорівнює власній частоті другої парціальної системи, амплітуда вимушених коливань втулки дорівнює нулю. У теорії коливань це явище отримало назву антирезонанса, а схеми, подібні наведеним на рис.3, близькі до схем динамічних гасителів коливань маси т. У дисипативних системах явище антирезонанса кілька згладжується демпфірувальними силами.[11] (2.32):
(2.32):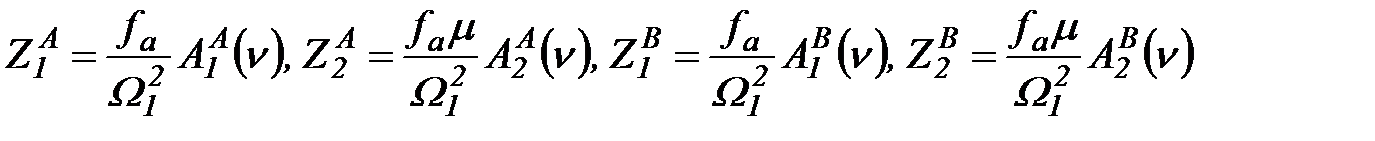 . (2.45)
. (2.45) відраховується від її недеформованого стану. Якщо амплітуда вимушених коливань втулки перевищить
відраховується від її недеформованого стану. Якщо амплітуда вимушених коливань втулки перевищить  , то на напівперіоді відходу втулки від опорного диска торцевий стик буде розкриватися. Щільність стику не порушується за умови
, то на напівперіоді відходу втулки від опорного диска торцевий стик буде розкриватися. Щільність стику не порушується за умови 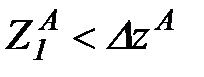 . Для деякого спрощення будемо вважати, що коливання вала відбуваються щодо незміщеного статичного положення:
. Для деякого спрощення будемо вважати, що коливання вала відбуваються щодо незміщеного статичного положення:  . З формули (1) випливає, що це можливо при
. З формули (1) випливає, що це можливо при  . В цьому випадку
. В цьому випадку  , а умова збереження контакту з урахуванням (2.44) приймає вигляд:
, а умова збереження контакту з урахуванням (2.44) приймає вигляд: . (2.46)
. (2.46)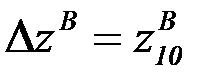 , і умова щільності контакту
, і умова щільності контакту . (2.47)
. (2.47) . [11]
. [11] , робоча частота обертання
, робоча частота обертання  . Діаметр вала (захисної рубашки) під ущільненням 120 мм;
. Діаметр вала (захисної рубашки) під ущільненням 120 мм; 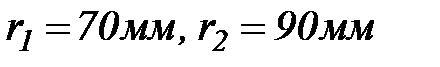 , перетин набивки 20х20 мм,
, перетин набивки 20х20 мм, 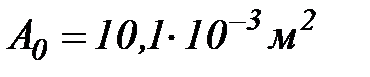 ; з досвіду приймаємо
; з досвіду приймаємо  Коеіфцієнти жорсткості пружніх елементів і набивки
Коеіфцієнти жорсткості пружніх елементів і набивки 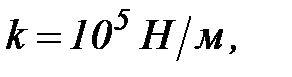
 ; коефіцієнт осьової жорсткості підшипників кочення
; коефіцієнт осьової жорсткості підшипників кочення 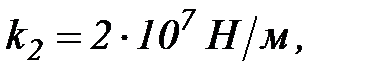
 . По формулам (2.27), (2.29),
. По формулам (2.27), (2.29),  ,
, 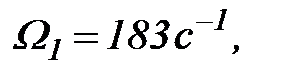
 ,
, 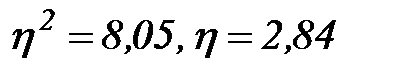 ,
, 
 .
. , рабоча частота обертання
, рабоча частота обертання 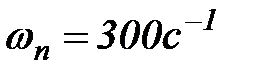 . Діаметр валу під ущільенням 40мм;
. Діаметр валу під ущільенням 40мм;  , перетин набивки 8х8 мм,
, перетин набивки 8х8 мм,  ; з досвіду приймаємо
; з досвіду приймаємо 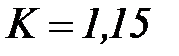 ;
; 
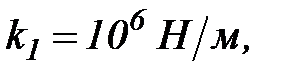

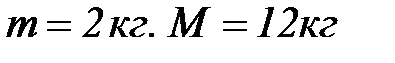 ,
,  По формулам (2.27), (2.29),
По формулам (2.27), (2.29), 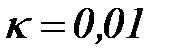 ,
,  ,
,  . [11]
. [11] так, щоб в процесі роботи забезпечувався необхідний контактний тиск
так, щоб в процесі роботи забезпечувався необхідний контактний тиск 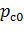 в парі тертя.
в парі тертя. . В цьому випадку розглядаються вимушені коливання втулки, що збуджуються осьовими коливаннями ротора і коливаннями ущільнюваного тиску.
. В цьому випадку розглядаються вимушені коливання втулки, що збуджуються осьовими коливаннями ротора і коливаннями ущільнюваного тиску.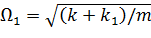 через велику жорсткість набивки, як правило, набагато більше робочої частоти обертання, тому резонансні режими рідкісне явище.
через велику жорсткість набивки, як правило, набагато більше робочої частоти обертання, тому резонансні режими рідкісне явище.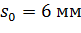 для набивки великого перерізу і
для набивки великого перерізу і  для другого прикладу.
для другого прикладу.


