
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вимушені коливання аксіально-рухомої втулки торцевого сальникового ущільненняСодержание книги
Поиск на нашем сайте
В загальному випадку динамічні моделі А і В представляють собою пов’язані двомасові системи, що здійснюють малі осьові коливання відносно положення статичної рівноваги. При цьому текучі значення перемінних можна представити у вигляді На підставі другого закону Ньютона для моделі А:
Виключивши рівняння рівноваги і опускаючи знак
де
Введемо оператор диференціювання по часу
де
Диференціальні оператори Подібно можна отримати систему рівнянь сумісних коливань моделі B:
Модель B відрізняється від моделі А двома коефіцієнтами особистого оператора
В даному випадку перехресний оператор пропорційний квадрату власної частоти першої парціальної системи, тобто зв'язок між парціальними системами є пружним. Як правило, маса рухомої сальникової втулки набагато менша за масу ротора. Вже цю обставину, як видно з систем (2.9), (2.11) можна розглядати як ознаку слабкої пов’язаності коливань ротора та втулки. Якщо не враховувати цей зв’язок, то з рівнянь, що залишилися Тут розглядаються коливання сальникової втулки, обумовлені заданими незалежними осьовими коливаннями ротора, які виступають як зовнішні кінематичні збурення. Ще одним джерелом збурень являються малі коливання ущільнюваного тиску відносно його сталого значення, яке, як правило, являється тиском нагнітання розглянутих насоса чи компресора: Будемо вважати, що обидва джерела збурень являються гармонічними функціями часу з частотою, рівною частоті обертання ротора, що характерно для відцентрових машин:
U – задана амплітуда осьових коливань вала,
Розглянемо перше рівняння системи (2.9) – модель А. Для гармонічних коливань оператор диференціювання
Відношення реакції системи до гармонічного впливу представляють відповідну частотну передаточну функцію:
де
Амплітуда і фаза отриманого комплексного числа виражаються формулами:
На резонансній частоті
Подібним чином для моделі В
Реакція аксіально-рухомої втулки на пульсації ущільнюваного тиску однакова для обох моделей. Щоб отримати амплітуду в безрозмірному вигляді, будемо приймати:
Формули (2.17), (2.19), (2.20) дають можливість оцінити розмірну амплітуду для будь-якої частоти обертання по заданим амплітудам гармонічних впливів
Формули (2.17) – (2.20) можна застосувати для механічних торцевих ущільнень, замінивши м’яку набивку з коефіцієнтом жорсткості Нормальна робота ущільнення характеризується присутністю постійного контакту між торцевими поверхнями сальникової набивки і опорного диска. Але при вимушених осьових коливаннях диска змінюються деформація набивки і контактний тиск, а при достатньо великих амплітудах можливе періодичне розкриття пари стику. Розкриття стику супроводжується різким збільшенням протікання, тому його потрібно уникати. Для моделі А величина стиснення набивки в рівноважному стані
Для моделі В
Останні нерівності можна використовувати для вибору відносної жорсткості
Числовий розрахунок Для того, щоб отримати деяке уявлення про динаміку аксіально – рухомої втулки реального торцевого сальникового ущільнення, розглянемо результати чисельного розрахунку амплітудних і фазових частотних характеристик двох різних за розмірами типових конструкцій. В обох прикладах статичний зсув ротора відсутній: 1. Насос двостороннього входу (типу Д) тиск нагнітання 2. Консольний конденсатний насос, тиск нагнітання Більшість подібних насосів по параметрам займають проміжне положення, тому розрахунок таких крайніх варіантів дозволяє судити про динаміку ущільнень з проміжними параметрами. На рисунках (2.2) та (2.3) приведені графіки амплітудних та фазових частотних характеристик для трьох значень показника затухання Попередня деформація пружних елементів і набивки, при яких торцевий стик не розкривається навіть на резонансних коливаннях, по умові (2.22), складає не менше 6,2 мм для моделі А, та не менше 5,5 мм для моделі В. Оскільки в розглянутих прикладах резонансні режими знаходяться далеко від номінальних, можна рекомендувати


Рисунок 2.2 – АЧХ як реакції на осьові коливання валу (Au(ν)) та на пульсації тиску(Af(ν)) в безрозмірному вигляді; фазова частотна характеристика (φ(ν)) для першої моделі


Рисунок 2.3 – АЧХ як реакції на осьові коливання валу (Au(ν)) та на пульсації тиску(Af(ν)) в безрозмірному вигляді; фазові частотні характеристики (φ(ν)) для другої моделі

Рисунок 2.4 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді; для першої моделі

Рисунок 2.5 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді, для другої моделі

Рисунок 2.6 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді при збільшенні коефіцієнтів жорсткостей пружини та набивки, для першої моделі

Рисунок 2.7 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді при збільшенні коефіцієнтів жорсткостей пружини та набивки, для другої моделі

Рисунок 2.8 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді при зменшенні одного коефіцієнту жорсткості сальникової набивки, для першої моделі

Рисунок 2.9 – АЧХ як реакції на осьові коливання валу (Au(ω)) та на пульсації тиску(Af(ω)) в розмірному вигляді при зменшенні одного коефіцієнту жорсткості сальникової набивки, для другої моделі
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-11; просмотров: 155; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.58.52.94 (0.011 с.) |

 ,
,  .
.
 ,
,
 , отримаємо пов’язану систему
, отримаємо пов’язану систему

 і представимо рівняння (2.7) в операторній формі:
і представимо рівняння (2.7) в операторній формі: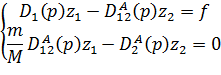



 ,
,  – особисті оператори ізольованих (парціальних) систем,
– особисті оператори ізольованих (парціальних) систем, 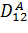 – перехресний оператор, що визначає пружно-демпферний зв’язок між коливаннями мас m, M. [8]
– перехресний оператор, що визначає пружно-демпферний зв’язок між коливаннями мас m, M. [8]
 і перехресним оператором:
і перехресним оператором: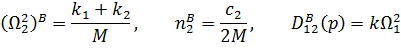
 ,
,  можна визначити вільні затухаючі коливання ротора. Через швидке затухання практичного інтересу вільні коливання не представляють. В тих рідких випадках, коли немає підстав нехтувати пов’язаністю коливань, можна отримати аналітичне рішення систем (2.9) та (2.11), користуючись відомими методами теорії коливань.
можна визначити вільні затухаючі коливання ротора. Через швидке затухання практичного інтересу вільні коливання не представляють. В тих рідких випадках, коли немає підстав нехтувати пов’язаністю коливань, можна отримати аналітичне рішення систем (2.9) та (2.11), користуючись відомими методами теорії коливань. . [8]
. [8]
 – амплітуда пульсуючого тиску. Для лінійних систем сумарна реакція рівна сумі реакцій на окремі збурення
– амплітуда пульсуючого тиску. Для лінійних систем сумарна реакція рівна сумі реакцій на окремі збурення
 ,
,  – амплітуди відповідних доданків вимушених коливань втулки.
– амплітуди відповідних доданків вимушених коливань втулки. , тому з першого рівняння системи (2.9) з урахуванням виразів (2.13) і (2.14) маємо
, тому з першого рівняння системи (2.9) з урахуванням виразів (2.13) і (2.14) маємо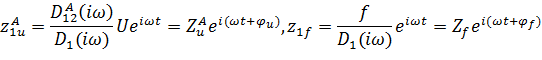
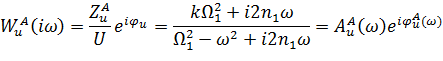
 ,
,  – амплітудні і фазова частотні характеристики вимушених коливань втулки під дією осьових коливань ротора. Розділимо дійсну і уявну частини (2.16) для цього помножимо чисельник і знаменник на спряжене знаменнику комплексне число, а також введемо безрозмірну частоту і показник затухання:
– амплітудні і фазова частотні характеристики вимушених коливань втулки під дією осьових коливань ротора. Розділимо дійсну і уявну частини (2.16) для цього помножимо чисельник і знаменник на спряжене знаменнику комплексне число, а також введемо безрозмірну частоту і показник затухання:  В результаті маємо
В результаті маємо



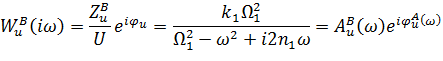
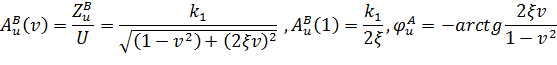

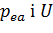 :
:
 на жорстке кільце з коефіцієнтом жорсткості, що прямує до безкінечності. При цьому
на жорстке кільце з коефіцієнтом жорсткості, що прямує до безкінечності. При цьому 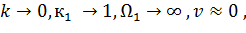 а безрозмірні амплітуди
а безрозмірні амплітуди 
 . [8]
. [8] відраховується від її недеформованого стану. Якщо амплітуда сумарних вимушених коливань втулки перевищить
відраховується від її недеформованого стану. Якщо амплітуда сумарних вимушених коливань втулки перевищить  , то на пів переході втулки від опорного диска торцевий стик буде розкриватися. В найбільш тяжкому випадку синфазних синхронних
, то на пів переході втулки від опорного диска торцевий стик буде розкриватися. В найбільш тяжкому випадку синфазних синхронних  коливань щільність стику не порушується при умові
коливань щільність стику не порушується при умові  . Для деякого спрощення будемо думати, що коливання вала відбуваються відносно незміщеного статичного положення
. Для деякого спрощення будемо думати, що коливання вала відбуваються відносно незміщеного статичного положення  . З формули (2.1) виходить, що це можливо при
. З формули (2.1) виходить, що це можливо при 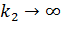 . В цьому випадку
. В цьому випадку 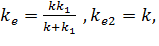 а умова збереження контакту з урахуванням (2.21) приймає вигляд:
а умова збереження контакту з урахуванням (2.21) приймає вигляд:
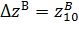 та умова щільності контакту
та умова щільності контакту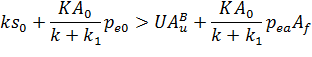
 .[8]
.[8]
 робоча частота обертання
робоча частота обертання  . Діаметр вала (захисної рубашки) під ущільненням 120 мм;
. Діаметр вала (захисної рубашки) під ущільненням 120 мм;  , переріз набивки 20х20 мм,
, переріз набивки 20х20 мм, 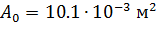 ; з досвіду приймається К=1,1. Коефіцієнти жорсткості пружних елементів та набивки
; з досвіду приймається К=1,1. Коефіцієнти жорсткості пружних елементів та набивки  По формулам (2.6), (2.8), (2.10),
По формулам (2.6), (2.8), (2.10), 
 , робоча частота
, робоча частота 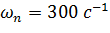 . Діаметр валу під ущільненням 40мм;
. Діаметр валу під ущільненням 40мм; 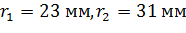 ; переріз набивки 8х8 мм,
; переріз набивки 8х8 мм,  ; з досвіду приймаємо К=1,15;
; з досвіду приймаємо К=1,15;  . По формулам (2.6), (2.8), (2.10)
. По формулам (2.6), (2.8), (2.10)  .
.
 . Безрозмірні частотні характеристики для обох прикладів майже не відрізняються, тому показані тільки фази
. Безрозмірні частотні характеристики для обох прикладів майже не відрізняються, тому показані тільки фази  для обох варіантів розглянутих конструкцій. Результати оцінки амплітуд вимушених коливань на робочій і на резонансній частотах приведені в таблиці для амплітуд збурень
для обох варіантів розглянутих конструкцій. Результати оцінки амплітуд вимушених коливань на робочій і на резонансній частотах приведені в таблиці для амплітуд збурень  і для показника затухання
і для показника затухання  .
.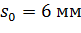 для набивки великого перерізу і
для набивки великого перерізу і  для другого прикладу.
для другого прикладу.


