
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Гармонічні коливання. Швидкість і прискорення під час гармонічних коливань.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нехай матеріальна точка m рівномірно рухається по колу радіуса А з кутовою швидкістю Рис. 29.1 X = Acos де
В цьому випадку x=Acos( де х – координата, що періодично змінюється, А – модуль її максимального значення координати (амплітуда), t – час, Періодом коливання Т називають проміжок часу, за який здійснюється одне повне коливання. Фізична величина Коливання, які здійснюються за законами синуса або косинуса, називаються гармонічними. Фізична система, яка здійснює коливання навколо положення рівноваги, називається осцилятором. Найпростіший гармонічний осцилятор – матеріальна точка, яка здійснює гармонічні коливання вздовж прямої. Швидкість V і прискорення а гармонічного осцилятора знайдемо, взявши першу, а потім другу похідну від функції х(t) за часом:
V=
a = . Тут A
Як видно із рівнянь (29.3), (29.4) та (29.5), величини X,V та а змінюються за гармонічним законом, але зсунуті одна відносно іншої за фазою: швидкість випереджає зміщення на
Порівнюючи формули (69.6) та (69.3), легко бачити, що a = Врахувавши те, що Acos(
Рівняння (29.8) є диференціальним рівнянням другого порядку. Воно називається кінематичним рівнянням коливального руху, а його розв’язком є рівняння (29.3). Підставивши в другий закон Ньютона (F=ma) замість а його значення (29.7), знайдемо силу, під дією якої здійснюються гармонічні коливання F = -m де k = m Із формули (29.9) видно, що сила Отже, тіло може здійснювати гармонічні коливання під дією пружних та квазіупружних сил. Коливання, які відбуваються в ізольованій системі, тобто під дією внутрішніх сил, називають вільними. Якщо внутрішні сили консервативні, то енергія коливальної системи залишається сталою, а коливання називають власними.
§ З0. Пружинний, математичний та фізичний маятники 1. Розглянемо власні коливання системи, яка складається з невеликого тіла масою m (наприклад кульки, надягненої на шпицю, яка може без тертя ковзати по ній) і пружинки жорсткістю к, один кінець якої з’єднаний із кулькою, а другий жорстко з’єднаний із шпицею (рис.30.1).
Сумістимо початок координат з центром мас кульки, коли вона знаходиться у стані рівноваги. Внаслідок зміщення кульки m із положення рівноваги на величину х, на тіло діятиме сила пружності F, напрямлена до положення рівноваги, яка згідно з законом Гука дорівнює: F=-kx, де к – коефіцієнт жорсткості пружини. Під дією сили F кулька набуде прискорення а. Згідно з другим законом Ньютона
Позначивши a = ·, Рівняння (30.1) є рівнянням гармонічного коливання. Його розв’язок має вигляд: x = де Як видно із (30.2), період коливань пружинного маятника пропорційний кореню квадратному із відношення маси тіла до жорсткості пружини.
2. Математичним маятником називають матеріальну точку, підвішену на тонкій невагомій, нерозтяжній нитці. Найкращим наближенням до моделі математичного маятника є металева кулька, підвішена на легкій нитці. Коли система перебуває у спокої, то сила тяжіння
Рис.30.2
Як видно з малюнка, силу F, яка повертає кульку в положення рівноваги, можна записати у вигляді: F=mgsin Якщо кут
Де L – довжина нитки, x – довжина дуги ОА. Підставивши у формулу (69.11) замість sin
Рівняння руху математичного маятника запишемо у вигляді:
або
Позначивши a= - Ми одержали рівняння, аналогічне рівнянню (30.1), розв’язком якого є рівняння (29.3). Циклічна частота
Отже, математичний маятник здійснює гармонічні коливання з періодом Т пропорційним кореню квадратному із відношення довжини маятника до прискорення вільного падіння. 3.Фізичним маятником називають тіло, здатне здійснювати коливання навколо нерухомої горизонтальної осі, яка не проходить через його центр мас (рис.30.3). У положенні рівноваги фізичного маятника його центр мас С знаходиться на Відхилимо маятник від положення рівноваги на кут
де Рис. 30.3 виконується приблизна рівність:
де Підставивши значення I Перепишемо рівняння (30.9) у такій формі:
Підставивши у Позначимо:
Врахувавши позначення (30.11), рівняння (30.10) можна записати у вигляді:
Розв’язком рівняння (30.12) є рівняння:
де
Прирівнявши праві і ліві частини рівняння (30.14) і (30.11), отримаємо:
Із рівняння (30.15) визначимо період коливань Т фізичного маятника:
Позначимо:
Врахувавши позначення (30.17), формулу (30.16) можна записати у вигляді:
Величину Точку ОІ, що міститься на лінії ОС на відстані
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1097; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 0. Виберемо прямокутну систему координат XOY, початок якої помістимо в центрі кола О. Спроектуємо точку m на осі координат. Якщо точка m рівномірно рухається по колу з кутовою швидкістю
0. Виберемо прямокутну систему координат XOY, початок якої помістимо в центрі кола О. Спроектуємо точку m на осі координат. Якщо точка m рівномірно рухається по колу з кутовою швидкістю  , то проекція точки m на осі координат здійснюватиме коливальні рухи вздовж осей ОХ та ОY відносно точки О. (рис.69.1). Нехай в початковий момент часу
, то проекція точки m на осі координат здійснюватиме коливальні рухи вздовж осей ОХ та ОY відносно точки О. (рис.69.1). Нехай в початковий момент часу  точка
точка  знаходилась на осі
знаходилась на осі  і кут
і кут  , утворений радіус-вектором точки m і віссю х, дорівнював нулю (
, утворений радіус-вектором точки m і віссю х, дорівнював нулю ( ).
).  Координата Х точки m в момент часу t, коли радіус Оm утворює довільний кут
Координата Х точки m в момент часу t, коли радіус Оm утворює довільний кут  з віссю ОХ, визначається рівнянням:
з віссю ОХ, визначається рівнянням: , (29.1)
, (29.1) – фаза коливань, А – максимальне значення координати Х, що дорівнює радіус-вектору Оm. Якщо в початковий момент часу t0=0 радіус om утворював з віссю ОХ кут
– фаза коливань, А – максимальне значення координати Х, що дорівнює радіус-вектору Оm. Якщо в початковий момент часу t0=0 радіус om утворював з віссю ОХ кут  , то в будь-який момент часу фазу коливань
, то в будь-який момент часу фазу коливань 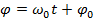 (29.2)
(29.2) його значення (29.2), одержимо:
його значення (29.2), одержимо: 0t+
0t+  – циклічна частота, Т – період коливання.
– циклічна частота, Т – період коливання. , обернена періоду
, обернена періоду  , яка чисельно дорівнює кількості коливань, що здійснюються за одиницю часу, називається частотою. Частота вимірюється у герцах (Гц). 1Гц=с-1. Рівняння (69.3) є рівнянням гармонічного коливання.
, яка чисельно дорівнює кількості коливань, що здійснюються за одиницю часу, називається частотою. Частота вимірюється у герцах (Гц). 1Гц=с-1. Рівняння (69.3) є рівнянням гармонічного коливання. =
=  - A
- A  A
A  (29.4)
(29.4) =
=  = - A
= - A  = A
= A  (29.5)
(29.5) – амплітуда швидкості точки, A
– амплітуда швидкості точки, A  – амплітуда прискорення. Врахувавши те, що
– амплітуда прискорення. Врахувавши те, що  , рівняння (29.5) запишемо у вигляді:
, рівняння (29.5) запишемо у вигляді: (29.6)
(29.6) , а прискорення випереджає зміщення на
, а прискорення випереджає зміщення на  (рис.29.2).
(рис.29.2).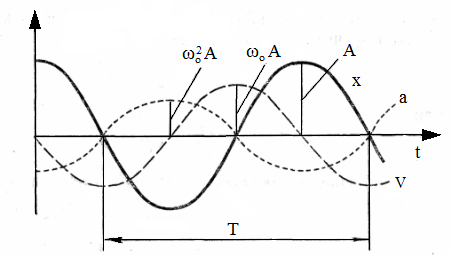
 . (29.7)
. (29.7)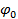 ) = x, формулу (69.6) запишемо у вигляді:
) = x, формулу (69.6) запишемо у вигляді: (29.8[l1]).
(29.8[l1]). x =- kx, (29.9)
x =- kx, (29.9) .
. пропорційна зміщенню і завжди напрямлена до положення рівноваги. Силою, яка задовільняє вказаним умовам, є сила пружності. Сили, не пружні за природою, але задовольняють умові F= -kx, називаються квазіпружними.
пропорційна зміщенню і завжди напрямлена до положення рівноваги. Силою, яка задовільняє вказаним умовам, є сила пружності. Сили, не пружні за природою, але задовольняють умові F= -kx, називаються квазіпружними.
 або
або  .
. , одержимо:
, одержимо: cos(
cos( ),
), . Підставивши у цю формулу замість
. Підставивши у цю формулу замість  , знайдемо вираз для обчислення періоду коливань пружинного маятника:
, знайдемо вираз для обчислення періоду коливань пружинного маятника: . (30.2)
. (30.2) зрівноважує силу натягу нитки
зрівноважує силу натягу нитки  . Якщо кульку відхилити на малий кут
. Якщо кульку відхилити на малий кут  , то рівнодійна F сили натягу
, то рівнодійна F сили натягу 
 . (30.3)
. (30.3) , (30.4)
, (30.4) його значення
його значення  , одержимо:
, одержимо: .
.
 . (30.5)
. (30.5) , рівність (30.5) запишемо у вигляді:
, рівність (30.5) запишемо у вигляді: . (30.6).
. (30.6).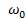 .=
.=  Підставивши у цю формулу замість
Підставивши у цю формулу замість  , знайдемо вираз для обчислення періоду коливань математичного маятника
, знайдемо вираз для обчислення періоду коливань математичного маятника .
. одній вертикалі з точкою підвісу О, але нижче від неї.
одній вертикалі з точкою підвісу О, але нижче від неї. , що повертатиме маятник до положення рівноваги. Під дією цього моменту маятник почне обертатися відносно осі О. Будемо вважати, що дією моменту сил опору можна знехтувати. За цих умов основне рівняння динаміки обертового руху фізичного маятника можна записати у вигляді:
, що повертатиме маятник до положення рівноваги. Під дією цього моменту маятник почне обертатися відносно осі О. Будемо вважати, що дією моменту сил опору можна знехтувати. За цих умов основне рівняння динаміки обертового руху фізичного маятника можна записати у вигляді: (30.7)
(30.7) – момент інерції відносно осі обертання, що проходить через точку О (у даному випадку вісь перпендикулярна до площини рисунка),
– момент інерції відносно осі обертання, що проходить через точку О (у даному випадку вісь перпендикулярна до площини рисунка),  – маса маятника, знак «мінус» вказує на те, що обертовий момент намагається повернути маятник у бік зменшення кута
– маса маятника, знак «мінус» вказує на те, що обертовий момент намагається повернути маятник у бік зменшення кута  такі малі, для яких
такі малі, для яких (30.8)
(30.8) із формули (30.8) у формулу 30.7), отримаємо:
із формули (30.8) у формулу 30.7), отримаємо: . (30.9)
. (30.9) = 0. (30.10)
= 0. (30.10) одиниці вимірювання
одиниці вимірювання  та
та  =
=  (30.12)
(30.12) (30.13)
(30.13) (30.14)
(30.14) (30.15)
(30.15) (30.16)
(30.16) (30.17)
(30.17) (30.18)
(30.18) називають зведеною довжиною фізичного маятника. Зведена довжина фізичного маятника – це довжина такого математичного маятника, період коливань якого дорівнює періоду коливань фізичного маятника.
називають зведеною довжиною фізичного маятника. Зведена довжина фізичного маятника – це довжина такого математичного маятника, період коливань якого дорівнює періоду коливань фізичного маятника.


