
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Хвилі. Фронт хвилі. Рівняння хвиліСодержание книги Поиск на нашем сайте
1. Коливання, що виникли в певній точці пружного середовища передаються сусіднім частинкам цього середовища внаслідок взаємодії між частинками і поширюються з деякою швидкістю Хвилі називаються поперечними, якщо коливання частинок середовища відбуваються в напрямі, перпендикулярному до напряму поширення хвилі. Якщо коливання частинок середовища відбуваються в напрямі, паралельному до напряму поширення хвилі, то хвиля називається поздовжньою. Лінія, яка вказує напрям поширення хвилі, називається променем. У пружному середовищі під час поширення повздовжніх хвиль виникають і поширюються деформації стиску і розтягу, а під час поширення поперечних хвиль виникають і поширюються деформації зсуву. На рис. 36.1 показано миттєве розташування точок середовища в поперечній (а) і поздовжній хвилях (б).
Хвильові збурення, поширюючись, охоплюють все нові і нові області середовища. Геометричне місце точок простору, до яких дійшов хвильовий процес в даний момент часу, називається фронтом хвилі. Геометричне місце точок, в яких коливання відбувається в однаковій фазі, називають хвильовою поверхнею. Хвильових поверхонь у даній хвилі можна провести безліч, а фронт хвилі один. Фронт хвилі – це найвіддаленіша від джерела хвильова поверхня у даний момент часу. Хвильові поверхні, як і фронт хвилі, переміщаються з швидкістю поширення хвилі. Якщо хвильова поверхня має форму сфери, то хвилю називають сферичною. Якщо хвильові поверхні є площини, то хвилю називають плоскою. На рисунку 36.2 зображено хвильові поверхні сферичної (а) і плоскої (б) хвилі. Джерелом сферичних хвиль є точкові джерела коливань. На великих відстанях від точкового джерела невеликі ділянки хвильової поверхні можна вважати плоскими. Довжиною хвилі
де T- період коливань,
Якщо відоме положення фронту хвилі в деякий момент часу
Користуючись принципом Гюйгенса, можна отримати закони відбивання та заломлення хвиль на межі поділу двох середовищ. Рекомендуємо читачеві зробити це самостійно. В даному параграфі подано лише отримані результати. Закони відбивання і заломлення хвиль на межі рис. 36.3[l4] поділу двох середовищ: 1) промінь, що падає на межу поділу двох середовищ, промінь відбитий від цієї межі, і перпендикуляр, поставлений в точку падіння до межі поділу двох середовищ, лежать в одній площині (рис.62.4); 2) кут падіння дорівнює куту відбивання (
3) в ідношення синуса кута падіння до синуса кута заломлення є величина стала для даних двох середовищ і називається відносним показником заломленн я[l5].
Кутом падіння (відбивання, заломлення) називають кут між перпендикуляром, поставленим в точку падіння, і променем, що падає на поверхню поділу двох середовищ (променем відбитим, заломленим променем). Відносний показник заломлення показує, у скільки разів швидкість поширення хвиль у першому середовищі більша, ніж швидкість поширення хвиль у другому середовищі. Тому формулу (36.1) можна записати у вигляді:
де середовищі, . 2. Нехай джерело хвиль, що знаходиться в точці О, є гармонічним:
Поширюючись в пружному середовищі, до будь-якої точки М з координатою r коливання від джерела дійдуть з запізненням на деякий проміжок часу
де Рівняння (36.3) є рівнянням плоскої хвилі, воно описує коливання будь-якої точки в будь-який момент часу. Якщо згасання немає, то амплітуда вздовж променя Оr однакова в усіх точках. Амплітуда коливань сферичної хвилі зменшується із збільшенням віддалі r від джерела. Враховуючи те, що
рівняння (36.3) можна записати у вигляді:
або
Під час поширення хвилі частинки речовини не переміщаються вздовж напрямку поширення хвилі, вони лише коливаються відносно положення рівноваги. Коливальний рух від частинки до частинки даного середовища передається з певною швидкістю, яка називається фазовою швидкістю. Наприклад, в поперечній хвилі синусоїда, що показує положення частинок середовища в момент часу . V =
Швидкість поширення хвилі залежить від пружних властивостей середовища і його густини. Швидкість поширення поперечних хвиль визначається формулою: V = де Е – модуль Юнга, Синусоїдальна хвиля, яка характеризується однією частотою, називається монохроматичною. Реальна хвиля, обмежена в часі і просторі (наприклад, хвильовий імпульс зображений на рис.36.6), не є синусоїдальною хвилею і характеризується певним набором частот. Оскільки всі хвильові процеси обмежені в просторі і часі, то строго монохроматичних хвиль в природі не існує.
Хвиля називається плоскополяризованою, якщо коливання частинок середовища відбуваються в одній площині. Поляризованими можуть бути лише поперечні хвилі.
|
||||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 1030; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |

 . Процес поширення коливань в середовищі називають хвильовим процесом, або хвилею.
. Процес поширення коливань в середовищі називають хвильовим процесом, або хвилею.
 називається віддаль між двома хвильовими поверхнями, коливання в яких відбувається з різницею фаз 2
називається віддаль між двома хвильовими поверхнями, коливання в яких відбувається з різницею фаз 2  . За час, що дорівнює періоду коливань, фронт хвилі переміщається в однорідному середовищі на віддаль, що дорівнює довжині хвилі
. За час, що дорівнює періоду коливань, фронт хвилі переміщається в однорідному середовищі на віддаль, що дорівнює довжині хвилі  , або
, або  .
.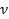 – частота коливань.
– частота коливань. і швидкість поширення хвилі V, то положення фронту в наступний момент часу
і швидкість поширення хвилі V, то положення фронту в наступний момент часу  можна визначити, застосувавши принцип Гюйгенса. Згідно з цим принципом, всі точки хвильової поверхні
можна визначити, застосувавши принцип Гюйгенса. Згідно з цим принципом, всі точки хвильової поверхні  , через які проходить фронт хвилі в момент часу
, через які проходить фронт хвилі в момент часу  в момент часу
в момент часу  однорідному ізотропному середовищі вторинні хвилі є сферичними.
однорідному ізотропному середовищі вторинні хвилі є сферичними. );
); (36.1)
(36.1)
 =
= 
 – швидкість поширення хвиль в першому Рис. 36.4
– швидкість поширення хвиль в першому Рис. 36.4 – швидкість поширення хвиль у другому середовищі.
– швидкість поширення хвиль у другому середовищі.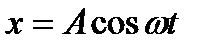 (36.2)
(36.2) , тому коливання в даній точці відставатимуть за фазою від коливань джерела:
, тому коливання в даній точці відставатимуть за фазою від коливань джерела: , (36.3)
, (36.3)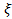 - узагальнена координата, t- час, V- швидкість поширення фази коливань (фазова швидкість).
- узагальнена координата, t- час, V- швидкість поширення фази коливань (фазова швидкість). =
=  =
=  ,
, ),
), ). (36.4)
). (36.4) зміститься на віддаль
зміститься на віддаль  (стрілками показано напрям швидкостей частинок). Отже, швидкість поширення фази коливань (наприклад, гребеня В) можна визначити, поділивши переміщення
(стрілками показано напрям швидкостей частинок). Отже, швидкість поширення фази коливань (наприклад, гребеня В) можна визначити, поділивши переміщення  .
.
 ,
, – густина середовища, у якому поширюється хвиля.
– густина середовища, у якому поширюється хвиля.


