
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Додавання однаково напрямлених гармонічних коливань. Биття. Поняття про гармонічний аналізСодержание книги
Поиск на нашем сайте Одна і та ж матеріальна точка може брати участь одночасно у двох і більше коливальних рухах. Якщо коливальна система бере участь у двох або більше коливальних рухах, то внаслідок накладання цих коливань виникає складний коливальний рух. У цьому випадку зміщення точки від положення рівноваги дорівнює алгебраїчній сумі зміщень кожного коливального руху. Задача знаходження сумарного коливального руху називається додаванням коливань. Розглянемо декілька простих випадків додавання коливальних рухів. 1. Знайти рівняння руху матеріальної точки, яка бере участь у двох однаково напрямлених коливальних рухах з однакової частоти:
Якщо точка бере участь у двох коливальних рухах, що відбуваються вздовж однієї прямої, то її сумарний рух відбуватиметься вздовж тієї самої прямої. Будемо розв’язувати дану задачу за допомогою векторної діаграми. Виберемо полюс О через який проведемо вісь Х. З полюса О відкладемо вектори ОА1 та ОА2 так, щоб їх модулі дорівнювали амплітудам коливальних рухів, а кути, які вони утворюють з віссю х дорівнювали б початковим фазам
Нехай вектор Рис.[l3] 34.1 Рух, що виникає внаслідок додавання двох коливальних рухів теж буде гармонічним коливанням, і його рівняння матиме вигляд:
де А – амплітуда сумарного коливального руху, З рисунку 34.1 видно, що A2=A12+A22+2A1A2cos(
З (34.4) видно, що амплітуда сумарного коливання залежить від різниці фаз складових коливань. Якщо
де Е1 і Е2 – енергії складових коливань. Енергія сумарного коливання також залежить від різниці початкових фаз складових коливань. 2. Якщо коливання
відбуваються з різними частотами, то вектори
Рівняння (34.6) описує періодичні коливання з середньою частотою
У зв’язку з тим, що період модуля косинуса дорівнює
У випадку, коли частоти
Внаслідок накладання періодичних коливань з різними частотами сумарний процес також буде періодичним, якщо ці частоти відносяться, як цілі числа. На рисунку 34.3 зображено результат накладання коливань з частотами 3. Можлива і обернена задача: негармонічне коливання подати у вигляді суми гармонічних коливань. Згідно з теоремою Фур’є, будь-яке періодичне коливання з частотою
де
Практично можна передати особливості будь-якого складного коливального процесу, підібравши суму кінцевої кількості гармонік, тобто розклавши коливання в спектр. Коливальні спектри характеризуються не тільки набором частот, але і амплітудою складових коливань. Складні коливання можна розкласти на прості гармонічні коливання не тільки математично, але й експериментально. За допомогою набору резонаторів визначають частоти гармонічних коливань, що входять до складу періодичного коливання. Резонатор – це коливальна система, що реагує на зовнішні гармонічні коливання, частота яких збігається з частотою власних коливань резонатора.
|
||
|
Последнее изменение этой страницы: 2016-04-07; просмотров: 701; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

 . (34.1)
. (34.1) . (34.2)
. (34.2) і
і  відповідно. В цьому випадку
відповідно. В цьому випадку  і
і 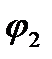 - кути, які утворюють дані вектори з віссю ОХ в початковий момент часу t0=0.
- кути, які утворюють дані вектори з віссю ОХ в початковий момент часу t0=0.
 і
і  обертаються відносно точки О з кутовою швидкістю
обертаються відносно точки О з кутовою швидкістю  . В цьому випадку проекції точок А1 і А2 на вісь х здійснюватимуть коливальні рухи, що описуються рівняннями (71.1) і (71.2). Сумарне зміщення у будь-який момент часу дорівнює сумі незалежних зміщень х=х1+х2. Оскільки вектори
. В цьому випадку проекції точок А1 і А2 на вісь х здійснюватимуть коливальні рухи, що описуються рівняннями (71.1) і (71.2). Сумарне зміщення у будь-який момент часу дорівнює сумі незалежних зміщень х=х1+х2. Оскільки вектори  і
і  обертаються з однаковими кутовими швидкостями
обертаються з однаковими кутовими швидкостями 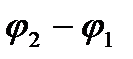 з часом не змінюється і вектор
з часом не змінюється і вектор  =
=  .
. , (34.3)
, (34.3) – його початкова фаза.
– його початкова фаза. . (34.5)
. (34.5) (n=0,1,2...), то А=А1+А2. Коли
(n=0,1,2...), то А=А1+А2. Коли 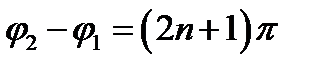 , то коливання х1 і х2 відбуваються у протилежних фазах, а амплітуда сумарного коливання дорівнює
, то коливання х1 і х2 відбуваються у протилежних фазах, а амплітуда сумарного коливання дорівнює  . Повна енергія сумарного коливання:
. Повна енергія сумарного коливання: ,
, ,
,  (34.5)
(34.5) і
і 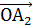 обертатимуться з різними кутовими швидкостями (рис.34.1) і кут
обертатимуться з різними кутовими швидкостями (рис.34.1) і кут  між ними буде змінюватися з часом. В цьому випадку амплітуда сумарного коливання також змінюватиметься з часом (див. 34.4) і сумарне коливання не буде гармонічним. Якщо
між ними буде змінюватися з часом. В цьому випадку амплітуда сумарного коливання також змінюватиметься з часом (див. 34.4) і сумарне коливання не буде гармонічним. Якщо  , то використавши формули перетворення суми тригонометричних функцій у їх добуток
, то використавши формули перетворення суми тригонометричних функцій у їх добуток  , одержимо:
, одержимо: . (34.6)
. (34.6) і амплітудою, що періодично змінюється з часом:
і амплітудою, що періодично змінюється з часом: . (71.7)
. (71.7) , то період зміни амплітуди
, то період зміни амплітуди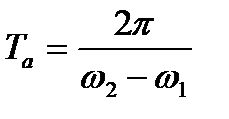 .
. і
і  близькі за величинами, виникає явище, що називається биттям, яке можна розглядати як періодичне коливання з пульсуючою амплітудою (рис.34.2).
близькі за величинами, виникає явище, що називається биттям, яке можна розглядати як періодичне коливання з пульсуючою амплітудою (рис.34.2).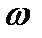 і
і  .
. (розкласти в ряд Фур’є):
(розкласти в ряд Фур’є): (34.8)
(34.8) – стала величина, член
– стала величина, член  – основне коливання (перша гармоніка), останні – вищі гармоніки. Сукупність цих гармонік утворює спектр коливання
– основне коливання (перша гармоніка), останні – вищі гармоніки. Сукупність цих гармонік утворює спектр коливання  . Склад спектру залежить від вигляду періодичної функції
. Склад спектру залежить від вигляду періодичної функції  . У найпростішому випадку спектр може складатись із невеликої кількості гармонік. Представлення періодичної функції у вигляді суми (34.8) називають гармонічним аналізом. Гармонічний аналіз застосовують для дослідження складних коливань.
. У найпростішому випадку спектр може складатись із невеликої кількості гармонік. Представлення періодичної функції у вигляді суми (34.8) називають гармонічним аналізом. Гармонічний аналіз застосовують для дослідження складних коливань.



