
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрична оптика як граничний випадок хвильової оптикиСодержание книги
Поиск на нашем сайте Хвильова оптика розглядає світло як процес поширення електромагнітних (світлових) хвиль у просторі. Всі задачі оптики можна розв'язати на основі хвильових уявлень. Однак це вимагає застосування громіздкого математичного апарата. Ще задовго до з'ясування хвильової природи світла вчені користувалися геометричними методами розв'язування задач на побудову зображень у дзеркалах і лінзах, а також під час розрахунку оптичних приладів. Ці методи становлять зміст геометричної оптики (яку ще називають променевою), в якій явища поширення світла і принципи дії оптичних приладів вивчають на основі уявлень про світлові промені. Основними поняттями геометричної оптики є промінь і пучок. У ній розглядаються: падіння, відбивання і заломлення променів; розбіжні, збіжні і паралельні пучки променів; хід променів у призмі, лінзі, мікроскопі, телескопі тощо. Чи означає це, що через лінзи і призми проходять не світлові хвилі, а промені, що від дзеркал відбиваються не хвилі, а промені? Що являють собою світлові промені? Яка їх фізична суть? Світлові промені — це лінії, вздовж яких поширюється світлова хвиля. Зміст понять промінь і пучок стає зрозумілим з такого досліду. Закриємо вікно картоном з кількома невеликими отворами і напустимо в кімнату трохи диму. Ми побачимо, що через отвори в картоні проривається сонячне світло у вигляді вузьких циліндричних пучків. Конічні пучки виникають, якщо помістити маленьку лампочку в непрозорий ящик з отворами. Циліндричні або конічні пучки, всередині яких поширюється світло, називають світловими пучками. Лінії, які вказують напрям поширення світла (у тому числі твірні і осі світлових пучків), називаюсь світловими променями. Геометрична оптика грунтується на трьох законах: прямолінійного поширення світла (в однорідному середовищі), відбивання і заломлення світла. Ці закони можна дістати з хвильової теорії як граничний випадок, коли розміри перешкод — на шляху світла набагато більші, ніж довжина світлової хвилі. Таким чином, використання поняття світлового променя зовсім не обов'язкове для розуміння того, що відбувається під час поширення світла. Воно просто полегшує розгляд. Уявлення та закони геометричної оптики справедливі лише тією мірою, в якій можна нехтувати явищами інтерференції світлових хвиль. Завдяки дифракції світлова хвиля трохи заходить за краї екрана і прямолінійність поширення світла порушується. Замість очікуваного за законами геометричної оптики пучка з різко окресленими твірними, дістанемо пучок, що розширюється, і в якого немає чіткої межі. Помітне свічення спостерігатиметься в конусі (мал. 133), кут розхилу якого можна визначити за формулою Отже, при наявності діафрагми (а вона завжди є в будь-якому оптичному приладі) Однак у ряді випадків розширення пучка порівняно з діаметром діафрагми, і тоді можна в першому наближенні дифракцією нехтувати. З малюнка 133 видно, що тах можна вважати, що Умова
Це і в критерій застосовності уявлень про світлові промені Іноді кажуть, що геометрична оптика справедлива, якщо розміри діафрагми набагато більші від довжини світлової хвилі. Однак цього недостатньо, тому що не враховується відстань L від екрана (місця спостереження) до діафрагми. При значних L умова (66.1) порушується і картина, що спостерігається на досліді, різко відрізняється від розрахованої за законами геометричної оптики, навіть коли отвір і досить великий. Отже, лише при виконанні умови перехід від хвильових уявлень до уявлень про світлові промені під час розгляду оптичних явищ, тобто геометрична оптика є граничним випадком хвильової оптики. Закони геометричної оптики Як відомо з попереднього параграфа, в основі геометричної оптики лежать три закони — прямолінійного поширення світла в однорідному середовищі, відбивання
і заломлення світла. Вони були спочатку встановлені дослідним шляхом. Однак хвильова теорія нояснюе їх елементарно, виходячи з принципу Гюйгенса. Закон прямолінійного поширення світла в однорідному середовищі. Нехай S — точкове джерело світле (мал. 134). На шляху світлової хвилі, яка виходить з цього джерела, знаходиться плоский екран NN з отвором А\Ао. Як допоміжну поверхню оберемо площину, що збігається з поверхнею екрана. Розглядатимемо всі точки цієї *пло щини в межах отвору Ці хвилі є сферичними поверхнями з центрами у відповідних вторинних джерелах. Оскільки в різні точки обраної нами допоміжної поверхні світлове збудження приходить в різні моменти часу, то радіуси сферичних поверхонь будуть різними. Так, наприклад, у точку А\ світло від джерела прийде раніше, ніж в Aj, відповідно вторинні хвилі з Очевидно, для всіх вторинних хвиль сума радіусів і відстаней їх центрів від джерела світла S має бути величиною сталою. Тому обгинаюча поверхня цих вторинних хвиль буде ділянкою кульової поверхні (на мал. 134 викреслена жирно) всередині конуса з твірними Закон відбивання світла. Нехай на межу розділення двох середовищ KL падає плоска хвиля і відбивається від неї (мал. 135). Падаючі промені А і В зображають крайні промені цієї хвилі. Згідно з принципом Гюйгенса всі точки
межі розділення середовищ можна розглядати як джерела елементарних хвиль. Перша елементарна хвиля виходить від точки С, куди раніше прийде падаюча хвиля. Далі почергово збуджуватимуться інші точки межі розділення, наприклад N, і, нарешті, останньою почне коливатися точка D, до якої падаюча хвиля дійде найпізніше. На малюнку 135 зображені положення елементарних хвиль для моменту досягнення падаючою хвилею точки D. Обгинаюча поверхня елементарних хвиль PD є фронтом відбитої хвилі. Ця пряма лежить у площині малюнка, тобто промінь падаючий і промінь відбитий лежать в одній площині, перпендикулярній до поверхні розділення середовищ, і утворює з межею розділення такий самий кут, як і падаюча хвиля. Дійсно, швидкості поширення падаючої хвилі і відбитих хвиль однакові. Отже, радіус найбільшої сфери повинен дорівнювати відстані, пройденій падаючою хвилею за час від моменту збудження першої до збудження останньої точки. З малюнка 135 видно, що кут падіння і кут відбивання відповідно дорівнюють кутам, утвореним фронтом падаючої і фронтом відбитої хвилі з площиною KL. З рівності трикутників CED і CQD виходить, що згадані кути дорівнюють один одному. Звідси випливає, що кут падіння променя світла дорівнює кутові відбивання. Ми застосували принцип Гюйгенса до пояснення відбивання світла для випадку плоскої хвиль Таким самим способом будується фронт відбитої сферичної хвилі. Така побудова показана на малюнку 136. Закон заломлення світла. Нехай плоска світлова хвиля, обмежена паралельними променями АС і BD (мал. 137), поширюючись в першому середовищі з швидкістю
поширення світлових хвиль vo інша, наприклад У той час, коли другий крайній промінь АС досягнув точки С, фронт хвилі займає положення СЕ і знаходиться від точки D на відстані ED. Цю відстань світлова хвиля пройде в першому середовищі з швидкістю За цей час вторинна хвиля з точки С, поширюючись у другому середовищі з швидкістю точку Д утворить з площиною
оскільки відношення (див. мал. 137). Аналогічно можна побудувати вторинну півсферичну хвилю з точки падіння променя MN на межу між середо- вищами, тобто з точки N. Радіус півсфери буде утворений дотичною до неї, проведеною з точки Д дорівнюватиме тому самому значенню, яке дає вираз (67.1):
оскільки відношення Звідси випливає, що дотична
тобто відношення синуса кута падіння світла до синуса кута заломлення дорівнює відношенню швидкості поширення світлових хвиль у першому середовищі до швидкості поширення хвиль у другому середовищі. Це відношення називають показником заломлення п другого середовища відносно першого, або відносним показником заломлення. Вираз (67.2) є законом заломлення світлових хвиль під час їх поширення з одного однорідного середовища в таке саме друге. Показник заломлення середовища відносно вакууму називають абсолютним показником заломлення цього середовища. Він дорівнює відношенню синуса кута падіння до синуса кута заломлення при переході світлового променя з вакууму в дане середовище. Відносний показник заломлення п можна виразити через абсолютні показники заломлення оскільки куумі, то
Середовище з меншим абсолютним показником заломлен- ] Закон заломлення світла не важко перевірити на дослі- ] ді. Закріпимо на оптичному диску прозорий півциліндр з матовою задньою поверхнею так, щоб середина плоскої поверхні збіглася з центром диска (мал. 138). Промінь від освітлювача йде вздовж радіуса диска і заломлюється j на плоскій поверхні півциліндра. Хід променя в склі видно і на матовій стінці півциліндра. Переміщенням освітлювача ] змінюють кут падіння променя і відповідно змінюється ] йут заломлення. Значення кутів падіння і заломлення |
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 750; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.012 с.) |

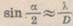 , де D — діаметр діафрагми (отвору в непрозорому екрані).
, де D — діаметр діафрагми (отвору в непрозорому екрані). закон прямолінійності поширення світла порупгувться.
закон прямолінійності поширення світла порупгувться.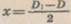 мале
мале , а при малих ку-
, а при малих ку-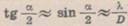 . Отже,
. Отже, 
 набуває вигляду,
набуває вигляду,  звідки випливав:
звідки випливав: (66.1)
(66.1) можливий
можливий
 , як джерела вторинних хвиль
, як джерела вторинних хвиль встигнуть за цей час поширитися далі, ніж із
встигнуть за цей час поширитися далі, ніж із  Отже, радіус сферичної поверхні, описаної навколо
Отже, радіус сферичної поверхні, описаної навколо  , буде більшим, ніж для
, буде більшим, ніж для 
 Всередині цього конуса світло від джерела поширюється так, ніби екран відсутній, а поза конусом світла немає.
Всередині цього конуса світло від джерела поширюється так, ніби екран відсутній, а поза конусом світла немає.
 , доходить до другого середовища, де швидкість
, доходить до другого середовища, де швидкість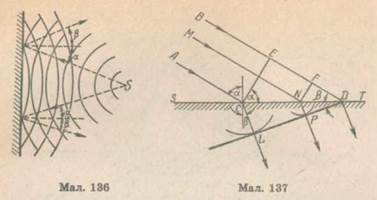
 Кут падіння світла на межу розділення середовищ ST позначимо а. Для визначення напряму поширення світла в другому середовищі побудуємо вторинні напівсферичні хвилі для моменту часу, коли крайній промінь BD досягне межі між середовищами в точці D.
Кут падіння світла на межу розділення середовищ ST позначимо а. Для визначення напряму поширення світла в другому середовищі побудуємо вторинні напівсферичні хвилі для моменту часу, коли крайній промінь BD досягне межі між середовищами в точці D. за час
за час 
 , утворить півсферу з радіусом
, утворить півсферу з радіусом  а дотична до цієї півсфери, проведена через
а дотична до цієї півсфери, проведена через кут
кут  , який визначається з рівності:
, який визначається з рівності:
 дорівнює синусу кута падіння
дорівнює синусу кута падіння і кут р\
і кут р\
 дорівнює синусу кута падіння.
дорівнює синусу кута падіння. до півсфери з центром в N суміщається з дотичною
до півсфери з центром в N суміщається з дотичною  і, отже, є обгинаючою вторинних хвиль. Таким чином, фронт світлової хвилі в другому середовищі буде площиною LDy і в ньому світлова хвиля поширюватиметься у напрямі перпендикуляра до цієї площини, тобто під кутом заломлення
і, отже, є обгинаючою вторинних хвиль. Таким чином, фронт світлової хвилі в другому середовищі буде площиною LDy і в ньому світлова хвиля поширюватиметься у напрямі перпендикуляра до цієї площини, тобто під кутом заломлення  . З рівності (67.1) випливає, що
. З рівності (67.1) випливає, що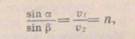 (67.2)
(67.2) першого і другого середовищ. Дійсно,
першого і другого середовищ. Дійсно,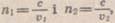 де с — швидкість світла у ва~
де с — швидкість світла у ва~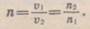 (67.3)
(67.3)


