
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Поняття про спектр негармонійнихСодержание книги
Поиск на нашем сайте Коливань і про гармонічний аналіз Періодичних процесів У реальних системах коливання можуть розглядатися як гармонічні лише з певним ступенем наближення; вони носять більш складний характер. Спостерігаються коливання настільки складні за формою, що описати кожне з них одним гармонічним законом не можна. Наприклад, не підпорядковані гармонічному закону сейсмічні коливання земної кори під час землетрусів. Жоден коливальний процес у природі чи в техніці не триває нескінченно довго, а має початок і кінець у часі. Оскільки коливальний процес обмежений у часі, він не є гармонічним. Будь-яке реальне коливання відбувається з поступовою витратою енергії руху на роботу проти сил тертя і на випромінювання, а тому не є гармонічним. Спостерігаються в природі коливальні процеси, які тривають дуже довго. Прикладом коливань такого роду можуть бути періодичні зміни напруги між різними ділянками людського тіла, які виникають в результаті роботи серця. Графік залежності «вироблюваної» серцевими м'язами напруги від часу називається електрокардіограмою (мал. 41). Вона дуже мало схожа на синусоїду (чи косинусоїду), тобто коливання біострумів є негармоніч-ними. Із складними негармонічними коливаннями мають справу в радіотехніці. Часто такі коливання є результатом додавання кількох гармонічних коливань з різними частотами, амплітудами, фазами тощо. Природно поставити запитання: якщо в результаті додавання простих гармонічних коливань виникають складні, різноманітні за формою результуючі коливання, то чи не можна подати складні коливання як суму простих гармонічних? Наприклад, на малюнку 42 зображено жир-
ною лінією коливання явно не гармонічне. Але його можна дістати, додаючи гармонічні коливання з частотами вання можна подати у вигляді суми * основного тону», який відповідає частоті Виявляється, розкладання складного коливання на ряд простих гармонічних коливань з частотами, кратними частоті складного коливання, яку називають основною частотою, можливе завжди. Причому, для кожного конкретного виду коливання розкладання можна здійснити єдиним способом. Закони такого розкладання сформулював у минулому столітті французький вчений Фур'є у вигляді теореми, яка відіграє величезну роль в сучасній науці й техніці Він довів, що майже будь-яка періодична функція з періодом 7і, задана на інтервалі від Цей ряд називають рядом Фур'є. Перша складова в ньому ною, гармонічною складовою розкладання з періодом Т, що дорівнює періоду функції Якби для аналізу періодичної функції f(t) однаково важливими були всі члени нескінченного тригонометричного ряду Фур'є (23.1), то гармонічний аналіз не мав би практичного значення, оскільки за його допомогою не можна було б здійснити жодних обчислень. Однак в дійсності амплітуда гармонік ряду Фур'є зі збільшенням номера п зменшується. Тому для практичної мети виявляється можливим використовувати замість нескінченного ряду тригонометричних функцій їх скінченне число. Кількість членів ряду Фур'є, які необхідно використати в розрахунках, визначається виглядом функції Результат гармонічного аналізу часто подають у вигляді так званого спектра складного коливання. Для цього на горизонтальній осі відкладають частоти складових гармонічних коливань, а вертикальними рисками (ординатами) позначають відповідні їм амплітуди. На спектрі не можна відобразити фази коливань, але нерідко буває достатньо знати частоти і амплітуди. Для прикладу розглянемо результат розкладання в спектр негармонічної періодичної функції, графік якої показано на малюнку 43. Періодичний коливальний процес, що його описує ця функція, можна дістати, наприклад, в електричному колі, яке складається з джерела струму з напругою U на вихідних клемах, вимикача К і резистора R (мал. 44). Якщо вимикач К замкнути і через інтервал часу т розімкнути, а потім через час Т після першого замикання знову замкнути на час т і таким чином повторювати процес вмикання і вимикання, то графік залежності напруги на резисторі R від часу матиме вигляд, показаний на малюнку 43. Амплітудний спектр гармонічних складових періодичної послідовності прямокутних імпульсів до 10-ї гармоніки показано на малюнку 45.
Гармонічний спектр складного коливання, який містить лише невелику кількість простих коливань і графік якого складається з окремих ординат, називається лінійчастим. Якщо спектр містить прості коливання практично всіх частот, він називається суцільним і графік його будується у вигляді кривої, яка обгинає верхівки ординат. Розкладання на прості гармонічні коливання виявляється можливим не лише для періодичних, а й для типово неперіодичних процесів (окремий імпульс, затухаючі коливання тощо). Неперіодичний процес можна подати як суму нескінченно великої кількості гармонічних коливань з амплітудами, які змінюються безперервно з усіма частотами. Розкладання складного коливання на прості (гармонічні) або, інакше кажучи, знаходження його гармонічного спектра є основним прийомом аналізу складного коливання. В імпульсній техніці гармонічний аналіз дає можливість виконувати розрахунки електричних кіл під час проходження ними електричних сигналів складної форми, застосовуючи прості правила розрахунку електричних кіл для його гармонічних складових. Часто гармонічний аналіз складних коливань здійснюють за допомогою спеціальних спектральних приладів — гармонічних аналізаторів. ? 1. У чому полягав суть методу гармонічного аналізу періодичних функцій? 2. Що такс спектр складного коливання і який вигляд має лінійчастий спектр негармонійного коливання? КОРОТКІ ПІДСУМКИ Й ВИСНОВКИ 1. Періодичні зміни заряду, сили струму й напруги
2. Основне рівняння вільних електромагнітних коли
3. Електромагнітні коливання високої частоти можна 4. Важливим прикладом вимушених електромагнітних 5. визначається рівністю 6. Діючі значення сили струму і напруги змінного 7. На конденсаторі коливання Він є опором реактивним, тобто в колі з ємністю відбуваються періодичні перетворення енергії струму і не відбувається її поглинання. 8. На котушці індуктивності коливання напруги випе
9. Закон Ома для кола змінного струму з послідовно
10. Потужність змінного струму на ділянці кола визна 11. коливального контуру сили струму під час резонансу різко зростають напруги на конденсаторі і котушці індуктивності. Під час резонансу зсув фаз між струмом і напругою стає рівним нулю.
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 361; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.229.80 (0.01 с.) |



 і
і  , причому
, причому  . Таким чином, дане складне коли-
. Таким чином, дане складне коли- , і «обертонам, який відповідає частоті
, і «обертонам, який відповідає частоті 
 , може бути
, може бути  розкладена в нескінченний тригонометричний ряд гармонічних функцій з певними амплітудами і фазами, частоти яких кратні основній частоті і сума яких дав функцію
розкладена в нескінченний тригонометричний ряд гармонічних функцій з певними амплітудами і фазами, частоти яких кратні основній частоті і сума яких дав функцію 
 :
: — стала складова функції
— стала складова функції  , незалежна від часу. Друга складова
, незалежна від часу. Друга складова  в першою, або основ-
в першою, або основ- . Третю складову називають другою гармонікою. її період вдвічі менший, ніж період функції
. Третю складову називають другою гармонікою. її період вдвічі менший, ніж період функції  . Період третьої гармоніки втричі менший, ніж Т і т. д.
. Період третьої гармоніки втричі менший, ніж Т і т. д. і заданою точністю обчислень.
і заданою точністю обчислень.

 (формула Томсона).
(формула Томсона). . Якщо опір контуру R
. Якщо опір контуру R
 . Сила
. Сила
 На активному опорі електромагнітна енергія генератора повністю перетворюється в інші види енергії. Коливання сили струму на цьому опорі збігаються за фазою з коливаннями напруги, а амплітуда сили струму
На активному опорі електромагнітна енергія генератора повністю перетворюється в інші види енергії. Коливання сили струму на цьому опорі збігаються за фазою з коливаннями напруги, а амплітуда сили струму
 сили струму випере
сили струму випере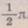 . Величину
. Величину 
 . Величину
. Величину 
 називають індуктивним опором. У випадку індуктивного опору також не відбувається споживання енергії генератора.
називають індуктивним опором. У випадку індуктивного опору також не відбувається споживання енергії генератора. називають повним опором кола.
називають повним опором кола. між напругою і струмом:
між напругою і струмом: 
 Різке зростання амплітуди вимушених коливань сили струму в коливальному контурі з малим активним опором — резонанс — відбувається тоді, коли збігаються частоти зовнішньої змінної напруги з власною частотою
Різке зростання амплітуди вимушених коливань сили струму в коливальному контурі з малим активним опором — резонанс — відбувається тоді, коли збігаються частоти зовнішньої змінної напруги з власною частотою . Одночасно із зростанням
. Одночасно із зростанням


