Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Принцип Гюйгенса — Френеля. Метод зон ФренеляСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Напрям поширення світлових хвиль, як і будь-яких інших, визначається за допомогою променів-ліній, перпендикулярних до хвильових поверхонь, які вказують напрям поширення енергії хвилі. Поняттям світлового променя ви широко користувались під час вивчення відкритих дослідним шляхом закону прямолінійного поширення світла в однорідному середовищі, законів відбивання і заломлення світла. В 9-му класі під час вивчення поширення механічних хвиль було введене поняття фронту хвилі або хвильової поверхні, яке повністю застосовне і у випадку світлових хвиль. Пригадаємо, що фронтом хвилі ми називали поверхню, яка є геометричним місцем точок, до яких хвилі доходять від джерела одночасно, або точок, коливання в яких здійснюються в однакових фазах. Якщо точкове джерело хвиль знаходиться в однорідному середовищі, то фронтом хвилі є сфера. Такі хвилі називають сферичними. Коли сферичний фронт хвилі досить віддалений від джерела, то невелику частину фронту хвилі з достатнім наближенням можна вважати плоскою. У таких випадках говорять про плоску хвилю. Напрям поширення сферичних чи плоских хвиль в однорідному середовищі збігається з напрямом перпендикулярів до фронту хвилі. Отже, вздовж перпендикулярів до фронту хвилі поширюється і енергія випромінювання. Використання понять променя і фронту хвилі істотно спрощує вивчення властивостей світлових хвиль. Цими поняттями ми будемо користуватися далі. Користуючись геометричними співвідношеннями між фронтом хвилі і променями, можна досить просто описувати поширення хвиль за методом, запропонованим у 1690 р. голландським фізиком X. Гюйгенсом. Він запропонував простий спосіб побудови фронту хвилі в момент часу і швидкість поширення хвиль у даному середовищі. Він міркував так: всі точки даного фронту хвилі коливаються однаково і зв'язані однаковим чином із своїми сусідами. Тому кожну точку середовища: до якої дійшов фронт хвилі, можна розглядати як нове джерело сферичних хвиль. Нехай у певний момент часу t фронт хвилі доходить до положення АВ (мал. 116); напрям його руху відомий. Точки, які лежать на лінії АВ, починають коливатися, і через малий інтервал часу \t навколо кожної з них утворюється невелика, так звана елементарна хвиля. У кожній точці простору навколо фронту хвилі АВ буде накладатися багато коливань, які йдуть від різних точок фронту хвилі. Спостереження і досліди показують, що коливатися будуть лише точки, які лежать на спільній зовнішній дотичній
А\В\ до елементарних хвиль. В інших точках відбувається взаємне послаблення коливань і хвилі гасять одна одну. Дальше поширення хаилі мсжна уявити як накладання елементарних хвиль, «сі виходять з точок поверхні А\В\ і т. д. Таким чином, для побудови фронту хвилі в момент часу t-\-\t треба кожну точку фронту АВ прийняти за центр сферичних хвиль, які поширюються вперед, потім побудувати з кожної точки фронт хвилі з радіусом r= v\t і провести обгинаючу всіх елементарних поверхонь. Ця обгинаюча і буде фронтом хвилі в момент часу t-f-At. Користуючись принципом Гюйгенса, можна прийти до висновку, що світло при проходженні через отвір у непрозорому екрані поширюється також і в області геометричної тіні екрана, тобто має місце відхилення світла від напряму прямолінійного пошиоення — дифракція. Однак у такому вигляді поинцип Гюйгенса не міг бути основою для кількісної теорії поширення хвиль і теорії дифракції, оскільки в ньому не враховувалась, різниця фаз хвиль, які додаються. Френель удосконалив принцип Гюйгенса тим, що врахував різницю фаз елементарних хвиль. Змінений таким способом принцип Гюйгенса називають принципом Г*мігенса — Фреяеля, Суть цього прзшщшу полягає в тому, що для кожного конкретного завдання слід певним способом розбити фронт хвилі- на ділянки (зони Френеля), які розглядаються як самостійні однакові джерела хвиль; азуідлітуда (й інтенсивність) хвилі в точці спостереження визначається як результат інтерференції хвиль, які ніби створюються окремими зонами. Ознайомимося у дещо спрощеному вигляді з методом зон і застосуємо його до пояснення дифракції світла на круглому отворі непрозорого екрана.
Нехай на отвір АС (мазі. 117, о) від джерела S падає сферична хвиля ABC. Щоб визначити, яку дію викличе хвильова поверхня у точці О екрана Е, проведемо з точки О конічні поверхні ОКТО, OMNO, VLQO до перетину з хвильовою поверхнею. Довжини твірних виберемо так, щоб
•у* і т. д., тобто щоб кожна наступна твірна збільшувалась на половину довжини хвилі. При такій побудові хвильова поверхня ABC ділиться на кільцеподібні зони, які при достатньому віддаленні точки О практично рівні між собою. Дія хіилі від двох сусідніх зон у точці О буде приблизно однаковою. Кожній точці першої зони відповідає точка другої зони, яка відрізняється на -у>. різницею ходу. Всі хвилі, які одночасно приходять в точку О від першої і другої зон, взаємно послаблюються. Точно так само дія третьої зони протилежна дії четвертої і другої зон і т. д. Якщо отвір ABC і точка спостереження О вибрані так, що на -хвильовій поверхні вміщуються лише дві зони Френеля, то в цій точці їх дія приведе до гасіння хвиль. Більша частина енергії випромінювання розподілиться навколо цієї точки у вигляді світлого кільця з темною плямою в центрі (мал. 117, б). Якщо на хвильовій поверхні поміщаються три зони, то в центрі буде світла пляма, оточена темним кільцем (мал. 117,6, справа і в). В загальному випадку, коли на хвильовій поверхні вміщується парне число зон, на екрані в центрі буде темна пляма, а при непарному числі зон — світла. Аналогічний розподіл освітленості на екрані можна спостерігати і у випадку дифракції на отворі у вигляді щілини. Для її пояснення хвильовий фронт необхідно розбити на зони Френеля у вигляді вузеньких смужок, паралельних краю щілини. Дифракційна картина складатиметься із світлих і темних плям, паралельних краю щілини. Зрозуміло, що приведені тут якісні міркування застосовні лише тоді, коли на отворі вкладається не дуже велике число зон Френеля. В принципі можна виготовити таку пластинку, яка перекривала б усі парні або всі непарні зони. Тоді всі хвилі приходитимуть в точку О у фазі і підсилюватимуть одна одну (хвилі, які приходять у протифазі, ми перекрили). Дістаємо прилад цілком аналогічний до лінзи. Все сказане вище свідчить про те, що освітленість у даній точці простору залежить не тільки від прямих променів від джерела, а й від частини простору, відкритої перед точкою. Висновок цей важливий тому, що розміри усіх оптичних деталей приладів обмежені і на оправах об'єктивів, дзеркал і лінз відбувається явище дифракції. Внаслідок цього світла точка за допомогою оптичного приладу зображається у вигляді дифракційних кружечків. Зображення двох точок джерела випромінювання буде роздільним, якщо їх дифракційні кружечки не зливаються. Розмір дифракційних кружечків вказує на межу розділення точок зображення для даного оптичного приладу (телескопа, мікроскопа). Явище дифракції світла на малих отворах обмежує роздільну здатність очей людини, тварин, птахів. Про те, що у хижих птахів зіркі очі, ходять легенди. Спробуємо дізнатися на основі явища дифракції світла, як бачить орел, що летить на висоті 1 км. Чи помітить він мишеня розміром в 3 см, чи лише зможе виявити його присутність, побачити точку? Припустимо, що діаметр зіниці ока орла дорівнює 10 мм. Мінімальний кут, при якому орел може бачити окремо дві точки предмета, дорівнює де редньому. Тоді видно під кутом менший, ніж той, при якому дифракція дає змогу орлові сприймати мишеня. Орел побачить його як одну точку і не розрізнить, а лише виявить, що там хтось є. Дифракція світла відбувається на предметах будь-яких розмірів, а не тільки співрозмірних з довжиною хвилі, як часто вважають. Але, у зв'язку з тим, що довжина світлової хвилі мала, інтерференційні максимуми, які виникають під час дифракції світла на великих перешкодах, розміщуються дуже близько один біля одного і їх інтенсивність швидко зменшується, тому дифракцію важко спостерігати. Якщо ж точка спостереження знаходиться далеко від перешкоди, то дифракція стає добре видимою.
? 1. Що таке фронт хвилі? Від чого залежить форма фронту хвилі? 2. У чому полягає метод побудови фронту хвилі, запропонований Гюй-генсом? 3. Яким уявленням Френель доповнив принцип Гюйгенса? 4. Для чого і як саме хвильова поверхня розбивається на зони Френеля? 5. У центрі інтерференційної картини від малого круглого отвору ноже спостерігатися або світла пляма (максимум), або темна пляма (мінімум). Від чого це залежить? Дифракційна решітка Спостереження дифракції від однієї щілини ускладнюється тим, що через вузьку щілину проникає дуже мало світла. Щоб дістати яскравішу дифракційну картину, треба пропускати світло через кілька паралельних вузьких щілин. У цьому випадку відбуватиметься інтерференція променів, які йдуть від усіх щілин, і найбільша освітленість буде в тих місцях екрана, куди приходитимуть промені в однаковій фазі. Тому для спостереження дифракції застосовують дифракційні решітки. Дифракційна решітка — це сукупність багатьох дуже вузьких щілин, розділених непрозорими проміжками (мал. 118). Решітки виготовляють у вигляді пластинок з прозорої твердої речовини, на поверхні яких алмазним різцем наносять паралельні штрихи. Штрихи розсіюють промені, а проміжки між штрихами відіграють роль шДлин. Розглянемо коротко дію дифракційної решітки. Нехай на решітку падає паралельний пучок монохроматичного світла (мал. 119). Всі щілини решітки випромінюють
вторинні хвилі в однаковій фазі. Кожна вторинна хвиля поширюється у всіх напрямах, однак можна виділити один певний напрям, який характеризується кутом Розглянемо результат накладання вторинних хвиль, які виходять від щілин дифракційної решітки. Нехай о означає ширину щілини, b — ширину непрозорої для світла ділянки між двома щілинами. Величину
Таким чином, різниця ходу залежить від кута
де k — ціле число. В напрямах, у яких різниця ходу між променями від сусідніх щілин решітки містить непарне число півхвиль, спостерігатимуться мінімуми, тобто умова спостереження дифракційного мінімуму запишеться:
(52.3) Вторинні хвилі, які поширюються у цих напрямах, гаситимуть одна одну. Оскільки положення максимумів і мінімумів залежить від довжини хвилі, то дифракційна решітка розкладає біле світло в спектр. *[ 1. Чому штрихи на дифракційній решітці мають бути розміщені щільно один біля одного? Чому їх мав бути багато? 2. Чи залежить положення головних максимумів дифракційної картини від кількості щілин в решітці? Вправа 5 1. Визначити довжину хвилі монохроматичного світла, якщо макси
2. На відстані
Дифракційний спектр Дифракційні решітки знайшли широке застосування для дослідження спектрального складу випромінювання. Досі ми вважали, що на дифракційну решітку падає монохроматичне світло, тобто світло лише однієї довжини хвилі. Оскільки положення дифракційного максимуму
одного, оскільки двох смуг першого порядку, які видно при використанні монохроматичного джерела світла, буде два спектри першого порядку, симетрично розташовані по обидва боки від центральної смуги і повернені до неї фіолетовим краєм. Далі будуть два спектри другого порядку і т. д. У спектрі першого порядку різниця ходу між коливаннями, які додаються, дорівнює
визначається умовою більшою довжиною хвилі (червоного кольору). Як ви вже знаєте (§ 52), положення головних світлих смуг визначається формулою:
де т — ціле число, яке визначає номер смуги (порядок спектра). Звичайно на практиці кути ф невеликі, а тому sin Для двох різних довжин хвиль будемо мати відповідно: (53.1) З формули (53.1) випливає, що кут між двома напрямами, які відповідають двом світлим смугам, утвореним двома різними довжинами хвиль, тобто практично відстань між цими смугами на екрані прямо пропорційна порядку спектра т і обернено пропорційна сталій решітки
У той час, коли у призматичному спектрі довгохвильова частина (червона) дуже стиснена порівняно з короткохвильовою (фіолетовою), у дифракційної решітки спектр розтягнутий рівномірно більший його порядок т. Знаючи сталу виміряти під мікроскопом) і вимірявши кут ф, можна дуже точно визначити довжину хвилі світла, яка дає світлу смугу певного порядку т під кутом
кладу, бажано виконувати спостереження в спектрі більшого порядку. Однак ряд обставин перешкоджає цьому: яскравість спектра зменшується зі збільшенням порядку і до того ж спектри високих порядків частково перекривають один одного. Ці дві обставини сильно обмежують можливість використання спектрів високого порядку. Дифракційна решітка Др є основною частиною деяких спектральних приладів — спектроскопів і спектрографів. Оптична схема спектрографа з дифракційною решіткою дуже проста (мал. 120). Вузька щілина, паралельна до щілин решітки, освітлюється джерелом світла. Ця щілина розміщена у головному фокусі першої лінзи спектрографа, яка створює плоскі хвилі, що падають на решітку. За решіткою стоїть друга лінза спектрографа, в головній фокальній площині якої спостерігаються спектри.
|
|||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 429; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.140.2 (0.013 с.) |

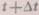 , якщо відоме положення фронту в момент t
, якщо відоме положення фронту в момент t

 ,
, — довжина хвилі денного світла в се-
— довжина хвилі денного світла в се- радіан. Мишеня
радіан. Мишеня радіан. Цей кут в 2 рази
радіан. Цей кут в 2 рази
 поставивши за дифракційною решіткою лінзу. У фокальній площині цієї лінзи зберуться всі промені, які йдуть паралельно її оптичній осі, інакше кажучи, накладуться вторинні хвилі, що виходять з щілин решітки.
поставивши за дифракційною решіткою лінзу. У фокальній площині цієї лінзи зберуться всі промені, які йдуть паралельно її оптичній осі, інакше кажучи, накладуться вторинні хвилі, що виходять з щілин решітки. прийнято називати періодом або сталою дифракційної решітки. Оскільки всі щілини знаходяться одна від одної на однаковій відстані, то різниці ходу променів від двох сусідніх щілин будуть при даному куті
прийнято називати періодом або сталою дифракційної решітки. Оскільки всі щілини знаходяться одна від одної на однаковій відстані, то різниці ходу променів від двох сусідніх щілин будуть при даному куті  однаковими для всієї дифракційної решітки і дорівнюють:
однаковими для всієї дифракційної решітки і дорівнюють: (52.1)
(52.1) 3 його зміною змінюється різниця ходу і відповідно результат накладання вторинних хвиль від щілин дифракційної решітки. В напрямах, де різниця ходу двох променів містить ціле число довжин хвиль, спостерігатимуться максимуми освітленості (дифракційні максимуми). У цьому випадку всі вторинні хвилі, накладаючись, підсилюють одна одну. Отже, умова спостереження дифракційного максимуму запишеться так:
3 його зміною змінюється різниця ходу і відповідно результат накладання вторинних хвиль від щілин дифракційної решітки. В напрямах, де різниця ходу двох променів містить ціле число довжин хвиль, спостерігатимуться максимуми освітленості (дифракційні максимуми). У цьому випадку всі вторинні хвилі, накладаючись, підсилюють одна одну. Отже, умова спостереження дифракційного максимуму запишеться так: (52.2)
(52.2)
 м, відхилився від нульового максимуму на кут
м, відхилився від нульового максимуму на кут
 м від екрана розташована дифракційна решітка
м від екрана розташована дифракційна решітка і синім
і синім 
 краями спектра на екрані.
краями спектра на екрані. залежить від довжини хвилі і є різним для різних довжин хвиль, то під час падіння на решітку немонохроматичного світла за решіткою головні смуги будуть в різних місцях. В результаті дістанемо спектр. Промені з більшою довжиною хвилі відхиляються сильніше, ніж промені з меншою довжиною хвилі, як це випливає з рівності
залежить від довжини хвилі і є різним для різних довжин хвиль, то під час падіння на решітку немонохроматичного світла за решіткою головні смуги будуть в різних місцях. В результаті дістанемо спектр. Промені з більшою довжиною хвилі відхиляються сильніше, ніж промені з меншою довжиною хвилі, як це випливає з рівності 
 . Таким чином, розміщення кольорів у дифракційному спектрі обернене до кольорів у призматичному спектрі. Центральна смуга, яка відповідає т = 0, буде ахроматичною — промені всіх кольорів підсилюватимуть один
. Таким чином, розміщення кольорів у дифракційному спектрі обернене до кольорів у призматичному спектрі. Центральна смуга, яка відповідає т = 0, буде ахроматичною — промені всіх кольорів підсилюватимуть один
 при будь-якому X. Замість
при будь-якому X. Замість , у спектрі другого порядку
, у спектрі другого порядку  і т. д. Спектри вищого порядку можуть частково перекривати сусідні спектри нижчих порядків. Число видимих повних спектрів
і т. д. Спектри вищого порядку можуть частково перекривати сусідні спектри нижчих порядків. Число видимих повних спектрів для променів з най-
для променів з най-
 і записана умова набуває вигляду
і записана умова набуває вигляду 

 і тим більше, чим
і тим більше, чим дифракційної решітки (її можна
дифракційної решітки (її можна . Здатність решітки розтягувати спектр пропорційна порядку останнього т. Тому, коли решітку застосовують для спектрального роз-
. Здатність решітки розтягувати спектр пропорційна порядку останнього т. Тому, коли решітку застосовують для спектрального роз-