
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дифракция. Метод зон Френеля. Дифракция на диске и отверстии.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Дифракция света – в узком, но наиболее употребительном смысле – огибание лучами света границы непрозрачных тел (экранов); проникновение света в область геометрической тени. Наиболее рельефно дифракция света проявляется в областях резкого изменения плотности потока лучей: вблизи каустик, фокуса линзы, границ геометрической тени и др. дифракция волн тесно переплетается с явлениями распространения и рассеяния волн в неоднородных средах. Дифракцией называется совокупность явлений, наблюдаемых при распространении света в среде с резкими неоднородностями, размеры которых сравнимы с длиной волны, и связанных с отклонениями от законов геометрической оптики. Между интерференцией и дифракцией нет существенных физических различий. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Явление дифракции объясняется с помощью принципа Гюйгенса, согласно которому каждая точка, до которой доходит волна, служит центром вторичных волн, а огибающая этих волн задает положение волнового фронта в следующий момент времени. Согласно принципу Гюйгенса, каждую точку фронта волны можно рассматривать как источник вторичных волн. Френель существенно развил этот принцип. · Все вторичные источники фронта волны, исходящей из одного источника, когерентны между собой. · Равные по площади участки волновой поверхности излучают равные интенсивности (мощности). · Каждый вторичный источник излучает свет преимущественно в направлении внешней нормали к волновой поверхности в этой точке. Амплитуда вторичных волн в направлении, составляющем угол α с нормалью, тем меньше, чем больше угол α, и равна нулю при · Для вторичных источников справедлив принцип суперпозиции: излучение одних участков волновой поверхности не влияет на излучение других (если часть волновой поверхности прикрыть непрозрачным экраном, вторичные волны будут излучаться открытыми участками так, как если бы экрана не было). Метод зон Френеля
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:
где A – амплитуда результирующего колебания, Величина Площадь одной зоны
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы. В то же время с увеличением номера зоны возрастает угол
. Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны. Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания
Отсюда следует:
Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда Интенсивность излучения Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность Так как радиус центральной зоны мал ( Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде. Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец. Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.
Дифракция от круглого отверстия: Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса
На продолжении этого перпендикуляра возьмем точку M и рассмотрим, что мы будем наблюдать на экране. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами
Таким образом, когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. выше. Естественно, что если
Дифракция от диска: Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск и тд. Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени).
|
|||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 486; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.007 с.) |

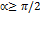 .
.
 от точки M (рис. выше). Точки сферы S, находящиеся на расстояниях
от точки M (рис. выше). Точки сферы S, находящиеся на расстояниях  ,
,  , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.
, и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля. .
.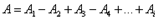 ,
,
 – амплитуда колебаний, возбуждаемая i -й зоной Френеля.
– амплитуда колебаний, возбуждаемая i -й зоной Френеля. зоны и угла
зоны и угла 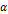 между нормалью к поверхности и прямой, направленной в точку M.
между нормалью к поверхности и прямой, направленной в точку M. .
.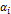 и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда
и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда 
 ,
,  , число зон
, число зон 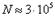 , а радиус первой зоны
, а радиус первой зоны  .
.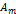 от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.
от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.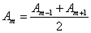 .
.
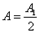 .
. .
. .
. ), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.
), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно. . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к.
. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к.  ). Интенсивность света увеличивается, если закрыть все четные зоны.
). Интенсивность света увеличивается, если закрыть все четные зоны. . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.
. Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.
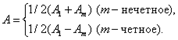
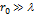 , то никакой дифракционной картины не будет.
, то никакой дифракционной картины не будет.




