
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Энергия эмв. Вектор умова. Вектор умова-пойтинга.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Импульс, массаэлектромагнитного пля (с выводом). Существование давления ЭМВ приводит к выводу о том, что электромагнитному полю присущ механический импульс. Выражая импульс как
отсюда
Это соотношение между массой и энергией ЭМП является универсальным законом природы, справедливым для любых тел независимо от их внутреннего строения. Импульс электромагнитного поля, связанного с движущейся частицей, – электромагнитный импульс – оказался пропорциональным скорости частицы υ, что имеет место и в выражении для обычного импульса m υ, где m – инертная масса заряженной частицы. Поэтому коэффициент пропорциональности в полученном выражении для импульса называют электромагнитной массой:
где е – заряд движущейся частицы, а – ее радиус. И даже если тело не обладает никакой иной массой, оказывается, что между импульсом и скоростью заряженной частицы существует соотношение:
Это соотношение как бы раскрывает происхождение массы – это электродинамический эффект. Движение заряженной частицы сопровождается возникновением магнитного поля. Магнитное поле сообщает телу дополнительную инертность – при ускорении затрачивается работа на создание магнитного поля, при торможении – работа против затормаживающих сил индукционного происхождения. По отношению к движущемуся заряду электромагнитное поле является средой, неотделимой от заряда. В общем случае можно записать, что полный импульс равен сумме механического и электромагнитного импульсов; возможно, что другие поля вносят и иные вклады в полную массу частицы, но, определенно, в полной массе есть электромагнитная часть:
Если учесть релятивистские эффекты сокращения длины и преобразования электрических и магнитных полей, то для электромагнитного импульса получается также релятивистски инвариантная формула:
Таким же образом изменяется релятивистский механический импульс. Излучение диполя. Диаграмма направленности излучения диполя. Интенсивность излучения. Чем вызвано ограничение энергии электронов при ускорении в бетатроне. Почему у БАКа малая кривизна траектории движения частиц. Любой заряд, движущийся ускоренно, излучает электромагнитную волну. Мощность
Рассмотрим электрический диполь с переменным дипольным моментом:
Амплитуда дипольного момента:
Такие колебания диполя могут возникнуть, например, при воздействии на молекулу (атом) вещества переменного электрического поля (рис.17.28): электронное облако перемещается относительно ядра вдоль оси OZ. Второй пример: колебания заряда на излучающей антенне (рис.17.29).
Средняя мощность излучения:
пропорциональна квадрату амплитуды дипольного момента и четвёртой степени частоты. Кроме того, мощность излучения неодинакова по всем направлениям. На расстояниях, много больших длины волны излучения
Последнее свойство объясняется законом сохранения энергии для сферической волны: чем дальше от излучателя, тем в большем шаровом слое распределяется энергия волны.
Интенсивность волны:
Можно привести ещё диаграмму направленности излучения точечного диполя (рис.17.31). Она даёт представление об интенсивности волны I, излучённой в данном направлении под углом
|
|||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 659; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |




 (поле в вакууме распространяется со скоростью света с), получим
(поле в вакууме распространяется со скоростью света с), получим



 ,
, 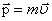 .
.
 излучения можно найти опять-таки из уравнений Максвелла; она пропорциональна квадрату заряда и квадрату его ускорения:
излучения можно найти опять-таки из уравнений Максвелла; она пропорциональна квадрату заряда и квадрату его ускорения: .
.
 – плечо диполя, изменяющееся гармонически с круговой частотой
– плечо диполя, изменяющееся гармонически с круговой частотой 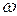 :
:






 , максимальные значения напряжённостей полей – электрического и магнитного – пропорциональны синусу угла
, максимальные значения напряжённостей полей – электрического и магнитного – пропорциональны синусу угла  между осью диполя и радиус-вектором данной точки и обратно пропорциональны расстоянию до диполя.
между осью диполя и радиус-вектором данной точки и обратно пропорциональны расстоянию до диполя.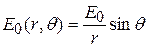
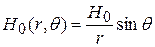

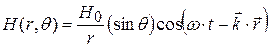


 волны не может иметь составляющих, перпендикулярных направлению колебаний диполя, а поскольку волна – поперечная, волны, излучённые в направлении колебаний (вдоль оси OZ) имели бы такую составляющую. Направления векторов напряжённостей электрического и магнитного полей в сферической волне изображены на рис.17.30:
волны не может иметь составляющих, перпендикулярных направлению колебаний диполя, а поскольку волна – поперечная, волны, излучённые в направлении колебаний (вдоль оси OZ) имели бы такую составляющую. Направления векторов напряжённостей электрического и магнитного полей в сферической волне изображены на рис.17.30:  – по касательной к «параллели»; векторы
– по касательной к «параллели»; векторы 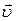 друг другу перпендикулярны и образуют правую тройку.
друг другу перпендикулярны и образуют правую тройку.



