
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнения волны для проекций e и h волн на оси координат.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Уравнения Максвелла для пустого пространства. Вывод волновых уравнений для электромагнитных волн (ЭМВ). Уравнения волны для проекций E и H волн на оси координат.
Энергия ЭМВ. Вектор Умова. Вектор Умова-Пойтинга.
Импульс, массаэлектромагнитного пля (с выводом). Существование давления ЭМВ приводит к выводу о том, что электромагнитному полю присущ механический импульс. Выражая импульс как
отсюда
Это соотношение между массой и энергией ЭМП является универсальным законом природы, справедливым для любых тел независимо от их внутреннего строения. Импульс электромагнитного поля, связанного с движущейся частицей, – электромагнитный импульс – оказался пропорциональным скорости частицы υ, что имеет место и в выражении для обычного импульса m υ, где m – инертная масса заряженной частицы. Поэтому коэффициент пропорциональности в полученном выражении для импульса называют электромагнитной массой:
где е – заряд движущейся частицы, а – ее радиус. И даже если тело не обладает никакой иной массой, оказывается, что между импульсом и скоростью заряженной частицы существует соотношение:
Это соотношение как бы раскрывает происхождение массы – это электродинамический эффект. Движение заряженной частицы сопровождается возникновением магнитного поля. Магнитное поле сообщает телу дополнительную инертность – при ускорении затрачивается работа на создание магнитного поля, при торможении – работа против затормаживающих сил индукционного происхождения. По отношению к движущемуся заряду электромагнитное поле является средой, неотделимой от заряда. В общем случае можно записать, что полный импульс равен сумме механического и электромагнитного импульсов; возможно, что другие поля вносят и иные вклады в полную массу частицы, но, определенно, в полной массе есть электромагнитная часть:
Если учесть релятивистские эффекты сокращения длины и преобразования электрических и магнитных полей, то для электромагнитного импульса получается также релятивистски инвариантная формула:
Таким же образом изменяется релятивистский механический импульс. Излучение диполя. Диаграмма направленности излучения диполя. Интенсивность излучения. Чем вызвано ограничение энергии электронов при ускорении в бетатроне. Почему у БАКа малая кривизна траектории движения частиц. Любой заряд, движущийся ускоренно, излучает электромагнитную волну. Мощность
Рассмотрим электрический диполь с переменным дипольным моментом:
Амплитуда дипольного момента:
Такие колебания диполя могут возникнуть, например, при воздействии на молекулу (атом) вещества переменного электрического поля (рис.17.28): электронное облако перемещается относительно ядра вдоль оси OZ. Второй пример: колебания заряда на излучающей антенне (рис.17.29).
Средняя мощность излучения:
пропорциональна квадрату амплитуды дипольного момента и четвёртой степени частоты. Кроме того, мощность излучения неодинакова по всем направлениям. На расстояниях, много больших длины волны излучения
Последнее свойство объясняется законом сохранения энергии для сферической волны: чем дальше от излучателя, тем в большем шаровом слое распределяется энергия волны.
Интенсивность волны:
Можно привести ещё диаграмму направленности излучения точечного диполя (рис.17.31). Она даёт представление об интенсивности волны I, излучённой в данном направлении под углом
Опыт Юнга
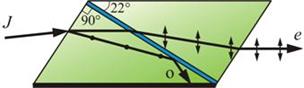
Свет от источника S, прошедший через узкую щель в экране А, падет на экран В с двумя щелями S 1 и S 2, расположенными достаточно близко друг к другу на расстоянии d. Эти щели являются когерентными источниками света. Интерференция наблюдается в области, в которой перекрываются волны от этих источников (поле интерференции). На экране Э мы видим чередование полос с максимумом и минимумом интенсивности света. Расстояние между двумя соседними максимумами называется расстоянием между интерференционными полосами, а расстояние между соседними минимумами – шириной интерференционной полосы. Этот опыт показывает, что интерференционная картина, создаваемая на экране двумя когерентными источниками света, представляет собой чередование светлых и темных полос. Главный максимум, соответствующий Зеркала Френеля
Источником служит узкая ярко освещенная щель S, параллельная ребру между зеркалами. Отраженные от зеркал пучки падают на экран, и в той области, где они перекрываются (поле интерференции), возникает интерференционная картина. От прямого попадания лучей от источника S экран защищен ширмой
Бипризма Френеля В данном интерференционном опыте, также предложенном Френелем, для разделения исходной световой волны на две используют призму с углом при вершине, близким к 180°. Источником света служит ярко освещенная узкая щель S, параллельная преломляющему ребру бипризмы
Можно считать, что здесь образуются два близких мнимых изображения S 1 и S 2источника S, так как каждая половина бипризмы отклоняет лучи на небольшой угол Билинза Бийе Аналогичное бипризме Френеля устройство, в котором роль когерентных источников играют действительные изображения ярко освещенной щели, получается, если собирающую линзу разрезать по диаметру и половинки немного раздвинуть
Прорезь закрывается непрозрачным экраном А, а падающие на линзу лучи проходят через действительные изображения щели
Интерферометры. Назначение. Явление интерференции волн находит разнообразное применение. Рассмотрим лишь некоторые примеры применения интерференции. · Тот факт, что расположение интерференционных полос зависит от длины волны и разности хода лучей, позволяет по виду интерференционной картины (или их смещению) проводить точные измерения расстояний при известной длине волны или, наоборот, определять спектр интерферирующих волн (интерференционная спектроскопия). Для осуществления таких измерений разработаны различные схемы высокоточных измерительных приборов, называемых интерферометрами (двух- и многолучевые). Незначительное перемещение одного из зеркал интерферометра приводит к смещению интерференционной картины, что можно использовать для измерения длин с точностью до 10-9м. Измерения с помощью интерферометра Майкельсона привели к фундаментальным изменениям представлений о пространстве и времени. Доказали отсутствие эфира. Послужили основой специальной теории относительности. · По интерференционной картине можно выявлять и измерять неоднородности среды (в т.ч. фазовые), в которой распространяются волны, или отклонения формы поверхности от заданной. · Явление интерференции волн, рассеянных от некоторого объекта (или прошедших через него) с «опорной» волной, лежит в основе голографии (в т.ч. оптической, акустической или СВЧ-голографии). · Интерференционные волны от отдельных «элементарных» излучателей используются при создании сложных излучающих систем (антенн) для электромагнитных и акустических волн. · Просветление оптики и получение высокопрозрачных покрытий и селективных оптических фильтров. Одной из важных задач, возникающих при построении различных оптических и антенных устройств СВЧ-диапазона, является уменьшение потерь (
Получение высокоотражающих диэлектрических зеркал Значительно повысить коэффициент отражения R зеркал можно, используя последовательность чередующихся диэлектрических слоев с высоким и низким показателями преломления (рис. справа). Интерферометры применяются как при точных измерениях длин, в частности в станко- и машиностроении, так и для оценки качества оптических поверхностей и проверки оптических систем в целом. Интерферометры широко используются в астрономии для создания радио- и оптических телескопов с высоким разрешением. Они позволяют заменить телескоп с большой апертурой (которая необходима для получения высокого разрешения) на решётку телескопов с меньшими апертурами, соединёнными по принципу интерферометра. Особым успехом интерферометры пользуются в радиоастрономии. Ввиду того, что к относительно низким радиочастотам предъявляются не такие строгие требования к дискретизации и оцифровке сигналов, существует возможность объединять радиотелескопы в сети РСДБ. Типы интерферометров: · Интерферометр Жамена · Интерферометр Маха — Цендера · Интерферометр Рождественского · Интерферометр шахтный · Интерферометр Майкельсона · Интерферометр гетеродинный · Интерферометр неравноплечный · Интерферометр Кёстерса · Интерферометр Тваймана-Грина · Интерферометр Чапского · Интерферометр Линника · Звёздный интерферометр Майкельсона · Интерферометр Рэлея · Интерферометр Саньяка · Интерферометр Физо · Резонатор Фабри — Перо (первоначально — интерферометр Фабри — Перо) · Сдвиговый интерферометр Опыты для наблюдения интерференции: - Опыт Юнга - Зеркало Ллойда - Зеркала Френеля - Бипризма Френеля - Интерференция в тонких пленках - Кольца Ньютона
Метод зон Френеля
Границей первой (центральной) зоны служат точки поверхности S, находящиеся на расстоянии Колебания, возбуждаемые в точке M между двумя соседними зонами, противоположны по фазе, так как разность хода от этих зон до точки M Поэтому при сложении этих колебаний, они должны взаимно ослаблять друг друга:
где A – амплитуда результирующего колебания, Величина Площадь одной зоны
Отсюда видно, что площадь зоны Френеля не зависит от номера зоны i. Это значит, что при не слишком больших i площади соседних зон одинаковы. В то же время с увеличением номера зоны возрастает угол
. Общее число зон Френеля, умещающихся на части сферы, обращенной в сторону точки M, очень велико: при Отсюда следует, что углы между нормалью к зоне и направлением на точку M у соседних зон примерно равны, т.е. что амплитуды волн, приходящих в точку M от соседних зон, примерно равны. Световая волна распространяется прямолинейно. Фазы колебаний, возбуждаемые соседними зонами, отличаются на π. Поэтому в качестве допустимого приближения можно считать, что амплитуда колебания
Отсюда следует:
Так как площади соседних зон одинаковы, то выражения в скобках равны нулю, значит результирующая амплитуда Интенсивность излучения Таким образом, результирующая амплитуда, создаваемая в некоторой точке M всей сферической поверхностью, равна половине амплитуды, создаваемой одной лишь центральной зоной, а интенсивность Так как радиус центральной зоны мал ( Если на пути волны поставить непрозрачный экран с отверстием, оставляющим открытой только центральную зону Френеля, то амплитуда в точке M будет равна Таким образом, принцип Гюйгенса–Френеля позволяет объяснить прямолинейное распространение света в однородной среде. Правомерность деления волнового фронта на зоны Френеля подтверждена экспериментально. Для этого используются зонные пластинки – система чередующихся прозрачных и непрозрачных колец. Опыт подтверждает, что с помощью зонных пластинок можно увеличить освещенность в точке М, подобно собирающей линзе.
Дифракция от круглого отверстия: Поставим на пути сферической световой волны непрозрачный экран с круглым отверстием радиуса
На продолжении этого перпендикуляра возьмем точку M и рассмотрим, что мы будем наблюдать на экране. Разобьем открытую часть волновой поверхности на зоны Френеля. Вид дифракционной картины зависит от числа зон Френеля, открываемых отверстием. Амплитуда результирующего колебания, возбуждаемого в точке М всеми зонами
Таким образом, когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке М будет больше, чем при свободном распространении волны; если четное, то амплитуда (интенсивность) будет равна нулю, как показано на рис. выше. Естественно, что если
Дифракция от диска: Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск и тд. Амплитуда световых колебаний в точке M равна половине амплитуды, обусловленной первой открытой зоной. Если размер диска невелик (охватывает небольшое число зон), то действие первой зоны немногим отличается от действия центральной зоны волнового фронта. Таким образом, освещенность в точке M будет такой же, как и в отсутствие экрана. Вследствие симметрии центральная светлая точка будет окружена кольцами света и тени (вне границ геометрической тени). Призма Николя
Это призма из исландского шпата, разрезанная по диагонали и склеенная канадским бальзамом Показатель преломления канадского бальзама лежит между значениями показателей Двойное лучепреломление объясняется анизотропией кристаллов. В таких кристаллах диэлектрическая проницаемость ε зависит от направления. В одноосных кристаллах диэлектрическая проницаемость в направлении оптической оси В зависимости от того, какая из скоростей Понятие теплового излучения и его отличие от других видов излучения. Равновесность теплового излучения. Закон Кирхгофа. Понятие абсолютно черного тела (АЧТ), излучательной способности тела. Спектральная излучательная способность АЧТ. Тепловое излучение – электромагнитное излучение, испускаемое веществом, возникающее за счет его внутренней энергии. Тепловое излучение бывает при любой температуре, человек только не ощущает его при меньшей температуре, чем температура тела, а при Равновесное излучение устанавливается в адиабатически замкнутой системе. Допустим, что равновесие нарушено, и тело излучает больше, чем поглощает. Тогда внутренняя энергия будет убывать, это уменьшит температуру тела, что противоречит адиабатичности системы. Следовательно, и излучение не будет равновесным. Равновесным может быть только тепловое излучение. Закон Кирхгофа Поток энергии (любых частот), испускаемый единицей поверхности излучающего тела в единицу времени во всех направлениях (в пределах телесного угла 4π), называется энергетической светимостью тела (R) [ R ] = Вт/м2. Излучение состоит из волн различной частоты (ν). Обозначим поток энергии, испускаемой единицей поверхности тела в интервале частот от ν до ν + dν, через d R ν. Тогда при данной температуре
где Опыт показывает, что лучеиспускательная способность тела зависит от температуры тела. Зная лучеиспускательную способность, можно вычислить энергетическую светимость:
Пусть на элементарную площадку поверхности тела падает поток лучистой энергии
называется поглощательной способностью тела. Она также сильно зависит от температуры. Не может быть больше единицы. Для АЧТ поглощательная способность равна 1. Тела, для которых Отношение лучеиспускательной к поглощательной способности не зависит от природы тела, оно является для всех тел одной и той же (универсальной) функцией частоты и температуры.
где т.е. универсальная функция Кирхгофа есть не что иное, как лучеиспускательная способность абсолютно черного тела. Луч, попавший внутрь, после многократных отражений обязательно поглощается, причём луч любой частоты
Разлагая это излучение в спектр, можно найти экспериментальный вид функции f (ν, T)(рис. 1.3), при разных температурах Т 3 > Т 2 > Т 1.
Площадь, охватываемая кривой, дает энергетическую светимость абсолютно черного тела при соответствующей температуре. Эти кривые одинаковы для всех тел. Максимум излучения (излучательной способности) с увеличением температуры смещается в сторону больших частот. Закон Вина. Формула Рэлея Джинса. Противоречия с опытом. Гипотеза Планка. Формула Планка.
где Эта формула дает хорошее согласие с опытом в коротковолновой части спектра и не годится для длинноволновой
Найдем максимум функции, то есть производную по ν и приравняем к нулю.
тогда
Это и есть закон смещения Вина. Смещение частоты в зависимости от температуры хорошо иллюстрируется экспериментальными кривыми, изображенными на рис. выше. Чаще закон смещения Вина записывают в виде
Это и есть формула Рэлея–Джинса.
Из формулы видно, что
Формула справедлива только в области малых частот и не согласуется с законом Вина. Попытка получить из формулы Рэлея–Джинса закон Стефана–Больцмана (R ~ T 4) приводит к абсурду:
Этот результат получил название «ультрафиолетовой катастрофы», так как с точки зрения классической физики вывод Рэлея–Джинса был сделан безупречно. Гипотеза Планка. Формула Планка. В своих расчетах Планк выбрал наиболее простую модель излучающей системы (стенок полости) в виде гармонических осцилляторов (электрических диполей) со всевозможными собственными частотами. Здесь Планк следовал Рэлею. Но Планку пришла мысль связать с энергией осциллятора не его температуру, а его энтропию. Термодинамическая вероятность В данном случае это число возможных способов распределения энергии между осцилляторами. Однако, такой процесс подсчета возможен, если энергия будет принимать не любые непрерывные значения, а лишь дискретные значения, кратные некоторой единичной энергии. Эта энергия колебательного движения должна быть пропорциональна частоте. Итак, энергия осциллятора должна быть целым кратным некоторой единицы энергии, пропорциональной его частоте.
где n = 1, 2, 3… Минимальная порция энергии
Окончательный вид формулы Планка:
Фотоэффект и его законы. I. При фиксированной частоте падающего света число фотоэлектронов, вырываемых из катода в единицу времени, пропорционально интенсивности света (сила тока насыщения пропорциональна энергетической освещенности Ee катода). II. Максимальная начальная скорость (максимальная начальная кинетическая энергия) фотоэлектронов не зависит от интенсивности падающего света, а определяется только его частотой ν. III. Для каждого вещества существует красная граница фотоэффекта, т.е. минимальная частота света Эффект Комптона.
Частота рассеянного света меньше частоты падающего света Разность
где l’ – длина волны рассеянного излучения, 20. Корпускулярно-волновой дуализм материи и его опытное обоснование. Гипотеза де Бройля. Дифракция электронов и нейтронов (опыты по дифракции электронов). Волновая функция и ее статический смысл. Амплитуда вероятностей. Различие между квантово-механической и статистической вероятностями. Уравнение Шредингера (стационарное). Частица в одномерной потенциальной яме. Уравнения Максвелла для пустого пространства. Вывод волновых уравнений для электромагнитных волн (ЭМВ). Уравнения волны для проекций E и H волн на оси координат.
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 792; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.222.161.245 (0.016 с.) |











 (поле в вакууме распространяется со скоростью света с), получим
(поле в вакууме распространяется со скоростью света с), получим



 ,
, 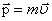 .
.
 излучения можно найти опять-таки из уравнений Максвелла; она пропорциональна квадрату заряда и квадрату его ускорения:
излучения можно найти опять-таки из уравнений Максвелла; она пропорциональна квадрату заряда и квадрату его ускорения: .
.
 – плечо диполя, изменяющееся гармонически с круговой частотой
– плечо диполя, изменяющееся гармонически с круговой частотой 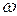 :
:






 , максимальные значения напряжённостей полей – электрического и магнитного – пропорциональны синусу угла
, максимальные значения напряжённостей полей – электрического и магнитного – пропорциональны синусу угла  между осью диполя и радиус-вектором данной точки и обратно пропорциональны расстоянию до диполя.
между осью диполя и радиус-вектором данной точки и обратно пропорциональны расстоянию до диполя.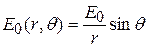
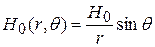

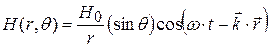


 волны не может иметь составляющих, перпендикулярных направлению колебаний диполя, а поскольку волна – поперечная, волны, излучённые в направлении колебаний (вдоль оси OZ) имели бы такую составляющую. Направления векторов напряжённостей электрического и магнитного полей в сферической волне изображены на рис.17.30:
волны не может иметь составляющих, перпендикулярных направлению колебаний диполя, а поскольку волна – поперечная, волны, излучённые в направлении колебаний (вдоль оси OZ) имели бы такую составляющую. Направления векторов напряжённостей электрического и магнитного полей в сферической волне изображены на рис.17.30:  – по касательной к «параллели»; векторы
– по касательной к «параллели»; векторы  друг другу перпендикулярны и образуют правую тройку.
друг другу перпендикулярны и образуют правую тройку.

 проходит через точку О. Вверх и вниз от него рас полагаются максимумы (минимумы) первого (
проходит через точку О. Вверх и вниз от него рас полагаются максимумы (минимумы) первого ( ), второго (
), второго ( порядков и т. д.
порядков и т. д.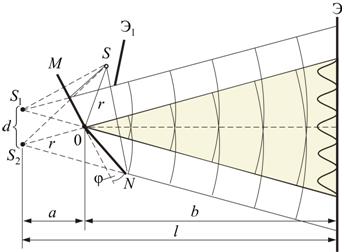
 . Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками
. Для расчета освещенности J экрана можно считать, что интерферирующие волны испускаются вторичными источниками  и
и  , представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на
, представляющими собой мнимые изображения щели S в зеркалах. Поэтому J будет определяться формулой двулучевой интерференции, в которой расстояние l от источников до экрана следует заменить на  , где -
, где -  расстояние от S до ребра зеркал, b - расстояние от ребра до экрана. Расстояние d между вторичными источниками равно:
расстояние от S до ребра зеркал, b - расстояние от ребра до экрана. Расстояние d между вторичными источниками равно:  . Поэтому ширина интерференционной полосы на экране равна:
. Поэтому ширина интерференционной полосы на экране равна:

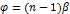 .
.
 и
и  и дальше перекрываются, образуя интерференционное поле.
и дальше перекрываются, образуя интерференционное поле. ) интенсивности света, мощности потока электромагнитной энергии при отражении от поверхностей линз, обтекателей антенн и пр. приборов, используемых для преобразований световых и радиоволн в разнообразных приборах фотоники, оптоэлектроники и радиоэлектроники. Для уменьшения потерь на отражение используется покрытие оптических деталей (линз) 3 пленкой 2 со специальным образом подобранными толщиной δ и показателем преломления n (рис. слева).
) интенсивности света, мощности потока электромагнитной энергии при отражении от поверхностей линз, обтекателей антенн и пр. приборов, используемых для преобразований световых и радиоволн в разнообразных приборах фотоники, оптоэлектроники и радиоэлектроники. Для уменьшения потерь на отражение используется покрытие оптических деталей (линз) 3 пленкой 2 со специальным образом подобранными толщиной δ и показателем преломления n (рис. слева).

 от точки M (рис. выше). Точки сферы S, находящиеся на расстояниях
от точки M (рис. выше). Точки сферы S, находящиеся на расстояниях  ,
,  , и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля.
, и т.д. от точки M, образуют 2, 3 и т.д. зоны Френеля. .
.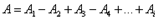 ,
,
 – амплитуда колебаний, возбуждаемая i -й зоной Френеля.
– амплитуда колебаний, возбуждаемая i -й зоной Френеля. зоны и угла
зоны и угла 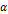 между нормалью к поверхности и прямой, направленной в точку M.
между нормалью к поверхности и прямой, направленной в точку M. .
.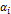 и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда
и, следовательно, уменьшается интенсивность излучения зоны в направлении точки M, т.е. уменьшается амплитуда 
 ,
,  , число зон
, число зон 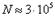 , а радиус первой зоны
, а радиус первой зоны  .
.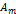 от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.
от некоторой m -й зоны равна среднему арифметическому от амплитуд примыкающих к ней зон, т.е.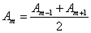 .
.
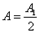 .
. .
. .
. ), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно.
), следовательно, можно считать, что свет от точки P до точки M распространяется прямолинейно. . Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к.
. Соответственно, интенсивность в точке M будет в 4 раза больше, чем при отсутствии экрана (т.к.  ). Интенсивность света увеличивается, если закрыть все четные зоны.
). Интенсивность света увеличивается, если закрыть все четные зоны. . Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.
. Экран расположен так, что перпендикуляр, опущенный из S на непрозрачный экран, попадает точно в центр отверстия.
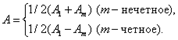
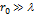 , то никакой дифракционной картины не будет.
, то никакой дифракционной картины не будет.

 и
и  для обыкновенного и необыкновенного лучей в исландском шпате (
для обыкновенного и необыкновенного лучей в исландском шпате (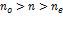 ). За счет этого обыкновенный луч претерпевает на прослойке бальзама полное внутреннее отражение и отклоняется в сторону. Необыкновенный луч свободно проходит через эту прослойку и выходит из призмы.
). За счет этого обыкновенный луч претерпевает на прослойке бальзама полное внутреннее отражение и отклоняется в сторону. Необыкновенный луч свободно проходит через эту прослойку и выходит из призмы. и в направлениях перпендикулярных к ней
и в направлениях перпендикулярных к ней  имеет разные значения.
имеет разные значения. или
или  больше, различают положительные и отрицательные одноосные кристаллы. При условии, когда
больше, различают положительные и отрицательные одноосные кристаллы. При условии, когда  – кристалл положительный,
– кристалл положительный,  – отрицательный.
– отрицательный. мы его не видим. Опыт показывает, что единственным видом излучения, которое может находиться в равновесии с излучающими телами, является тепловое излучение.
мы его не видим. Опыт показывает, что единственным видом излучения, которое может находиться в равновесии с излучающими телами, является тепловое излучение. ,
, - спектральная плотность энергетической светимости, или лучеиспускательная способность тела.
- спектральная плотность энергетической светимости, или лучеиспускательная способность тела.
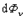 , обусловленный электромагнитными волнами, частоты которых заключены в интервале dν. Часть этого потока
, обусловленный электромагнитными волнами, частоты которых заключены в интервале dν. Часть этого потока  будет поглощаться телом. Безразмерная величина
будет поглощаться телом. Безразмерная величина
 и меньше единицы – серые тела.
и меньше единицы – серые тела. ,
,
 – универсальная функция Кирхгофа
– универсальная функция Кирхгофа


 и
и  – постоянные, которые Вин не расшифровал.
– постоянные, которые Вин не расшифровал.

 .
.
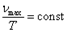 .
.
 , где постоянная Вина
, где постоянная Вина  .
.


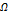 – число возможных микроскопических комбинаций, совместимое с данным состоянием в целом.
– число возможных микроскопических комбинаций, совместимое с данным состоянием в целом.
 ,
,
 где– постоянная Планка;
где– постоянная Планка;  и
и  .
.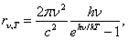 или
или 
 (зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.
(зависящая от химической природы вещества и состояния его поверхности), ниже которой фотоэффект невозможен.
 не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния j:
не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния j:
 – комптоновская длина волны (при рассеянии фотона на электроне
– комптоновская длина волны (при рассеянии фотона на электроне  ).
).


