
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругие волны в однофазных горных породахСодержание книги Поиск на нашем сайте
Акустический метод Одним из ведущих методов изучения разрезов скважин является акустический метод, основанный на измерения параметров упругого волнового поля в скважине. Метод предназначен для непосредственного изучения акустических параметров волнового поля горных пород пересечённых скважиной. Акустические параметры горных пород функционально связаны с физико-механическими свойствами, пористостью, структурными особенностями и характером насыщения. В обсаженных скважинах характеристики акустических сигналов также тесно связаны с условиями передачи упругих деформаций на границе цементного кольца с породой и с колонной. Эти обстоятельства создают предпосылки для эффективного применения этих зависимостей для решения широкого круга геофизических задач. В лекции описаны основные уравнения акустического метода, а также даны характеристики основных видов волн, возникающих в скважине и околоскважинном пространстве. Элементы теории упругости Действие внешних сил на тела, находящиеся в равновесии, компенсируют внутренние упругие силы, порождающие в телах упругие напряжения. Выделим в среде малый объем
где индекс n указывает направление, нормальное к площадке. На площадках, перпендикулярных координатным осям
В идеальных жидкостях и газах сдвиговая упругость отсутствует, в связи с чем касательные напряжения не возникают, вектора напряжений направлены навстречу действующей на рассматриваемый объем силе, т. е. численно равны давлению Р с обратным знаком. Условно считая давление тензором, запишем
где В процессе сейсмоакустических исследований среда подвергается воздействию внешних сил, приводящему к смещению ее частиц
где
Согласно (1.4б) сумма диагональных членов матрицы (1.4а)
где В цилиндрической системе координат удлинения (сжатия) обозначают
Линейную связь между тензором напряжения
где λ и µ — положительные величины, называемые константами Ламэ. Часто µ называют модулем сдвига, так как он определяет величину сдвига при данном касательном напряжении. Закон Гука для жидкостей и газа (µ=0) с учетом выражения (1.3) запишем в виде
где
где
где β — адиабатическая сжимаемость жидкости. Уравнения акустики Упругие волны во флюидах - жидкостях и газах - распространяются вследствие того, что движение частиц среды создает чередующиеся сжатия и разрежения, которые вызывают движение в следующем слое флюида. Поскольку флюиды обладают объемной упругостью и не обладают сдвиговой, возмущения передаются вдоль направления колебаний и во флюидах существуют только продольные волны. Твердые тела обладают как объемной, так и сдвиговой упругостью, и в них наряду с продольными волнами возникают поперечные. Основные явления, свойственные волнам различной природы, описываются универсальными математическими зависимостями. К ним относятся фазовая скорость υ, комплексное волновое число К, его составляющие — фазовая постоянная а и коэффициент поглощения b. Акустические характеристики изотропных сред описываются модулями перечисленных величин. Справедливы также дисперсионные соотношения, в соответствии с которыми наличие объемной частотной дисперсии скорости свидетельствует о поглощении, а наличие поглощения обусловливает объемную частотную дисперсию скорости. Кроме того, избыточное давление, создаваемое изучаемыми в сейсмоакустике волнами, мало, в связи с чем среда по отношению к ним линейна и волну произвольной формы можно представить суперпозицией гармонических волн. Поэтому, изучая особенности распространения упругих волн, будем, как и раньше, пользоваться гармоническими представлениями. Результат для волны произвольной формы можно получить, воспользовавшись преобразованиями Фурье. Большинство горных пород — насыщенные пористые среды (НПС), состоящие из твердой фазы (матрицы) и флюида – порозаполнителя. При сейсмоакустических исследованиях возмущения в среде а соответственно и смещения частиц, малы и можно считать, что разрывов в ней не возникает. В этом смысле горная порода - сплошная многофазная среда, упругие характеристики которой определяются характеристиками матрицы и флюида а также межфазными взаимодействиями. В тех случаях, когда объем порового пространства мал, породу можно условно считать однофазной. Упругие волны, распространяющиеся в реальных средах, постепенно затухают за счет расхождения фронтов и поглощения энергии — диссипации. На сейсмоакустических частотах основной механизм диссипации в однофазных средах — неравновесный теплообмен между участками сжатия и растяжения, а также трение в материале. В многофазных средах диссипация существенно возрастает за счет появления теплообмена между матрицей и флюидом, межфазного трения и некоторых других факторов. В целом диссипация в однофазных породах значительно меньше, чем в НПС, и при их изучении можно воспользоваться законами распространения волн в идеально упругих средах. Идеально упругие среды — среды без поглощения. Их волновое число имеет только действительную часть: К = а(ω). Фазовая скорость определяется по формуле υ = ω /а(ω) и не зависит от частоты. Поэтому волны акустического и сейсмического диапазонов частот распространяются в идеально упругих средах с одинаковыми скоростями. Неидеально упругие среды характеризуются поглощением, комплексным волновым числом и являются в этой связи диспергирующими: скорость и затухание в них — функции частоты. В общем случае скорость и затухание, связанное с поглощением, зависят от свойств горных пород, в связи, с чем их можно считать основными информационными параметрами упругих волн. Скорости, фазы, времена распространения волн на фиксированных базах называют кинематическими параметрами. Те параметры, которые связаны с энергией волн и характеризуют, в частности, их затухание, называют динамическими. На практике наиболее употребимым кинематическим параметром является интервальное время Δt — время прохождения волной пути, равного единице длины. Очевидно, что Δt = 1/υ. Наиболее употребимый динамический параметр — отношение амплитуд волн в двух точках, расположенных на разном расстоянии от излучателя. Скорость, затухание и частота гармонических волн в изотропных средах связаны дисперсионным уравнением вида Проиллюстрируем сказанное на простейшем примере распространения плоской волны давления в идеальной жидкости (газе). Под последней понимаем жидкость (газ), вязкость и теплопроводность которой равны нулю, и которую поэтому можно считать идеально упругой. При распространении волны частицы жидкости смещаются относительно положений равновесия - движутся. Известно, что любые движения жидкости описываются полной системой уравнении гидродинамики. Следовательно, упругая волна в жидкости также должна удовлетворять этим уравнениям. Полная система уравнений гидродинамики имеет вид:
где δ — плотность жидкости; Равенство (2.1а) называют уравнением движения (уравнением Эйлера). Оно характеризует движение частиц под действием сил упругости и сторонних сил и, как легко убедиться, выражает второй закон Ньютона в дифференциальной форме. Равенство (2.1б) называют уравнением неразрывности, поскольку оно получено в предположении, что в среде нет разрывов, и изменение массы в объеме V в отсутствии сторонних источников массы равно массе, прошедшей через поверхность, ограничивающую этот объем. Равенство (2.1в), называемое уравнением состояния, связывает давление и температуру жидкости с ее объемом. Уравнения, входящие в систему (2.1), нелинейны, а потому достаточно сложны. Поскольку нас интересуют только волны малых амплитуд, эти уравнения можно линеаризовать. Из курса математической физики известно, что в общем случае
Здесь первый член — локальное ускорение — характеризует изменение скорости в данном месте пространства, а последующие образуют конвективное ускорение, обусловленное смещением частиц из точки с одной скоростью в точку с другой скоростью. При сейсмоакустических исследованиях амплитуды волн а соответственно смещения частиц, малы, в связи с чем
Воспользовавшись линеаризованным уравнением состояния (1.9) для идеальной жидкости и повторно продифференцировав выражение (2.2б) по t, получим
Если положить плотность сторонних сил, в том числе сил трения, равными нулю, уравнение (2.2а) примет вид:
Подставив выражение (2.4) в (2.3), найдем волновое уравнение для акустического давления:
Давление, подобно другим параметрам плоской гармонической волны, распространяющейся вдоль оси x (при x >0), выражается соотношением:
Множитель
Итак, скорость в идеальной жидкости зависит только от свойств жидкости и не является функцией частоты. Кроме того, характерное для жидкости и газа отсутствие сдвиговой упругости предопределяет существование в них волн только одного типа — продольных. Несмотря на простоту формулы (2.7), она по структуре подобна другим формулам скорости упругих волн, в том числе и в твердых средах: в числителе под корнем — выражение, характеризующее жесткость (упругость) среды и, следовательно, скорость передачи напряжений от частицы к частице, в знаменателе — соответствующая плотность, характеризующая инерционность частиц. В бесконечно жесткой среде напряжения нарастали бы на бесконечно малых расстояниях, т.е. бесконечно быстро, и скорость стремилась к бесконечности. При стремлении к бесконечности массы, время, необходимое для изменения положения частиц, стремилось бы к бесконечности, а скорость — к нулю. При этом в обоих случаях к нулю стремилась бы и амплитуда смещения. То обстоятельство, что с увеличением плотности акустическая скорость в твердых однофазных телах обычно растет, а не падает, обусловлено тем, что при увеличении плотности реального вещества, жесткость растет быстрее плотности. Головные волны в скважине
Угол Поскольку в волне Головные волны Вследствие интерференции распределение энергии в спектре зарегистрированных колебаний отличается от ее распределения в спектре излученных колебаний. Подчеркиваются те частоты, для которых интерференция происходит в фазе, иными словами, для которых на участках ADB, ВЕС (см. рис. 2) укладывается целое число волн. Это явление называют конструктивной интерференцией. Поскольку отрезок АD для волны В общем случае видимая частота соответствует наименьшей частоте конструктивной интерференции. Определим ее.
Видимую частоту волны В реальных условиях диаметр скважины меняется, а прибор отклоняется от оси. Поэтому распределение энергии в спектре зарегистрированных колебаний, в известной степени, случайная величина и спектральный анализ сигналов с целью определения параметров пород целесообразно проводить по начальной части волновой картины, которая не осложнена конструктивной интерференцией. При распространении головных волн вдоль стенки скважины они затухают за счет расхождения и поглощения. На низких частотах расхождение монотипной волны пропорционально Интерференция волн затрудняет, а иногда делает невозможной их идентификацию. Рассмотрим в лучевом приближении положение фронтов прямых Допустим в момент времени t = 0 излучен импульс упругих колебаний, а в момент
Время прихода волны
Время прихода головной волны в точку, расположенную на расстоянии длины зонда
Зависимость времени прихода волны от расстояния
Сопоставление выражений (3.9) и (3.10) показывает, что при
монотипная волна обгоняет прямую. Аналогично можно найти годограф обменной волны и определить расстояние, при котором ее удастся зарегистрировать раньше, чем возникнет интерференция с прямой волной. Таким образом, существует принципиальная возможность регистрации не осложненных интерференцией головных волн в скважине. Их параметры характеризуют упругие свойства среды за стенкой скважины. Заключение Выше описанные закономерности появления различных типов волн, позволяют применять результаты акустических методов исследования скважин в следующих направлениях: 1. Получение данных при интерпретации данных сейсморазведки. 2. Литологическое расчленение разрезов скважин. 3. Оценка прочностных свойств горных пород 4. Выделение коллекторов, оценка их пористости и типа порового пространства. 5. Изучение качества обсадки скважины – цементометрия. 6. Исследования на месторождениях твёрдых полезных ископаемых, в инженерно-геологических и гидрологических скважинах. 7. Скважинное акустическое телевидение. 8. Акустические исследования в процессе бурения скважин. 9. Обнаружение зон АВПД. Акустический метод Одним из ведущих методов изучения разрезов скважин является акустический метод, основанный на измерения параметров упругого волнового поля в скважине. Метод предназначен для непосредственного изучения акустических параметров волнового поля горных пород пересечённых скважиной. Акустические параметры горных пород функционально связаны с физико-механическими свойствами, пористостью, структурными особенностями и характером насыщения. В обсаженных скважинах характеристики акустических сигналов также тесно связаны с условиями передачи упругих деформаций на границе цементного кольца с породой и с колонной. Эти обстоятельства создают предпосылки для эффективного применения этих зависимостей для решения широкого круга геофизических задач. В лекции описаны основные уравнения акустического метода, а также даны характеристики основных видов волн, возникающих в скважине и околоскважинном пространстве. Элементы теории упругости Действие внешних сил на тела, находящиеся в равновесии, компенсируют внутренние упругие силы, порождающие в телах упругие напряжения. Выделим в среде малый объем
где индекс n указывает направление, нормальное к площадке. На площадках, перпендикулярных координатным осям
В идеальных жидкостях и газах сдвиговая упругость отсутствует, в связи с чем касательные напряжения не возникают, вектора напряжений направлены навстречу действующей на рассматриваемый объем силе, т. е. численно равны давлению Р с обратным знаком. Условно считая давление тензором, запишем
где В процессе сейсмоакустических исследований среда подвергается воздействию внешних сил, приводящему к смещению ее частиц
где
Согласно (1.4б) сумма диагональных членов матрицы (1.4а)
где В цилиндрической системе координат удлинения (сжатия) обозначают
Линейную связь между тензором напряжения
где λ и µ — положительные величины, называемые константами Ламэ. Часто µ называют модулем сдвига, так как он определяет величину сдвига при данном касательном напряжении. Закон Гука для жидкостей и газа (µ=0) с учетом выражения (1.3) запишем в виде
где
где
где β — адиабатическая сжимаемость жидкости. Уравнения акустики Упругие волны во флюидах - жидкостях и газах - распространяются вследствие того, что движение частиц среды создает чередующиеся сжатия и разрежения, которые вызывают движение в следующем слое флюида. Поскольку флюиды обладают объемной упругостью и не обладают сдвиговой, возмущения передаются вдоль направления колебаний и во флюидах существуют только продольные волны. Твердые тела обладают как объемной, так и сдвиговой упругостью, и в них наряду с продольными волнами возникают поперечные. Основные явления, свойственные волнам различной природы, описываются универсальными математическими зависимостями. К ним относятся фазовая с
|
||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 509; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.011 с.) |

 , а в нем — площадку dS. Если на нее действует произвольно направленная сила dF, вектор напряжения на площадке
, а в нем — площадку dS. Если на нее действует произвольно направленная сила dF, вектор напряжения на площадке , (1.1)
, (1.1) ,
, 
 , в этом случае согласно формуле (1.1) действуют вектора напряжений
, в этом случае согласно формуле (1.1) действуют вектора напряжений  ,
,  ,
,  . Разложив вектор
. Разложив вектор  ,
,  ,
,  . Очевидно, что
. Очевидно, что  (1.2)
(1.2) , (1.3)
, (1.3) — тензор упругих напряжений в жидкости.
— тензор упругих напряжений в жидкости. . Возникающую при этом деформацию полностью определяет тензор
. Возникающую при этом деформацию полностью определяет тензор (1.4а)
(1.4а) при i = j — относительные удлинения (сжатия) бесконечно малых отрезков, которые до деформации были параллельны координатным осям;
при i = j — относительные удлинения (сжатия) бесконечно малых отрезков, которые до деформации были параллельны координатным осям;  (1.4б)
(1.4б) ,
, —изменение объема. Величину
—изменение объема. Величину  называют дилатацией.
называют дилатацией. ,
,  ,
,  , а сдвиговые деформации —
, а сдвиговые деформации —  ,
,  ,
,  . Их можно выразить через смещения:
. Их можно выразить через смещения: ;
;  ;
;  ;
; ;
;  ;
;  (1.5)
(1.5) и тензором деформации
и тензором деформации 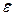 при температуре T=const выражает обобщенный закон Гука. Для изотропной среды он имеет вид
при температуре T=const выражает обобщенный закон Гука. Для изотропной среды он имеет вид (1.6)
(1.6) , (1.7)
, (1.7) —модуль всестороннего сжатия, играющий для жидкости роль константы Ламэ λ. Знак минус указывает на уменьшение объема с ростом давления. При характерных для сейсмоакустики слабых возмущениях
—модуль всестороннего сжатия, играющий для жидкости роль константы Ламэ λ. Знак минус указывает на уменьшение объема с ростом давления. При характерных для сейсмоакустики слабых возмущениях , (1.8)
, (1.8) — невозмущенная плотность среды;
— невозмущенная плотность среды;  — изменение плотности. Поэтому выражение (1.7) можно записать следующим образом:
— изменение плотности. Поэтому выражение (1.7) можно записать следующим образом: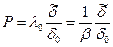 , (1.9)
, (1.9) или системой таких уравнений. Их получают, преобразуя систему волновых уравнений, которая, в свою очередь, является результатом преобразования полной системы уравнений гидродинамики. Решение дисперсионного уравнения (или системы уравнений) позволяет определить скорость и затухание как функцию частоты.
или системой таких уравнений. Их получают, преобразуя систему волновых уравнений, которая, в свою очередь, является результатом преобразования полной системы уравнений гидродинамики. Решение дисперсионного уравнения (или системы уравнений) позволяет определить скорость и затухание как функцию частоты. ; (2.1а)
; (2.1а) ; (2.1б)
; (2.1б) ; (2.1в)
; (2.1в) — скорость ее частиц;
— скорость ее частиц;  — плотность сторонних сил; Р, V, Т — соответственно давление, объем и температура.
— плотность сторонних сил; Р, V, Т — соответственно давление, объем и температура.
 . По этой же причине справедливы неравенства:
. По этой же причине справедливы неравенства:  ;
;  . где
. где  — вектор смещения частиц, связанный с их скоростью соотношением
— вектор смещения частиц, связанный с их скоростью соотношением  ;
;  — длина волны. Из сказанного следует, что
— длина волны. Из сказанного следует, что  и
и  , в связи с чем уравнения (2.1а) и (2.1б) в линеаризованном виде можно записать следующим образом:
, в связи с чем уравнения (2.1а) и (2.1б) в линеаризованном виде можно записать следующим образом: ; (2.2а)
; (2.2а) . (2.2б)
. (2.2б) . (2.3)
. (2.3) . (2.4)
. (2.4) (2.5)
(2.5) . (2.6)
. (2.6) , как и для электромагнитных волн, характеризует поглощение. Положив силы трения равными нулю, а температуру Т постоянной, мы заведомо приняли
, как и для электромагнитных волн, характеризует поглощение. Положив силы трения равными нулю, а температуру Т постоянной, мы заведомо приняли  . Из двух его решений
. Из двух его решений  одно дает скорость плоской волны, распространяющейся в положительном направлении оси х:
одно дает скорость плоской волны, распространяющейся в положительном направлении оси х: (2.7)
(2.7)
 Наряду с отраженной волной
Наряду с отраженной волной 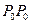 на стенке скважины образуется преломленная волна
на стенке скважины образуется преломленная волна  (рис. 2). Направления их волновых векторов связаны законом Снеллиуса, являющимся выражением принципа причинности, который в данном случае можно сформулировать как условие неразрывности фронтов отраженной и преломленной волн. На основе простых геометрических построений не трудно показать, что если это условие выполняется,
(рис. 2). Направления их волновых векторов связаны законом Снеллиуса, являющимся выражением принципа причинности, который в данном случае можно сформулировать как условие неразрывности фронтов отраженной и преломленной волн. На основе простых геометрических построений не трудно показать, что если это условие выполняется, 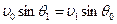 . Угол
. Угол 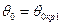 для которого
для которого 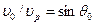 (соответственно
(соответственно 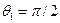 ), называют первым критическим. При углах падения
), называют первым критическим. При углах падения  имеет место полное внутреннее отражение, в связи, с чем возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью
имеет место полное внутреннее отражение, в связи, с чем возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью 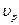 продольной волны в породе. Учитывая механизм образования, их, как и преломленные, обозначают
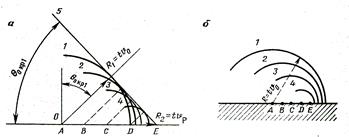
продольной волны в породе. Учитывая механизм образования, их, как и преломленные, обозначают 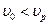 .
.
 Поскольку скорость головной волны
Поскольку скорость головной волны 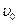 продольной волны в жидкости, в скважине возникает вторичная продольная волна, обозначаемая
продольной волны в жидкости, в скважине возникает вторичная продольная волна, обозначаемая 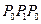 . Механизм ее образования можно пояснить на основе принципа Гюйгенса — Френеля. Для этого каждую точку стенки скважины, например A, В, С, D (рис. 3), следует считать источником волны
. Механизм ее образования можно пояснить на основе принципа Гюйгенса — Френеля. Для этого каждую точку стенки скважины, например A, В, С, D (рис. 3), следует считать источником волны 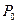 , возникающей в момент прохождения через эту точку фронта волны
, возникающей в момент прохождения через эту точку фронта волны 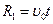 (окружности 1 на рис. 3, а и б). Аналогично волны, излученные из точек В, С, D, представляют сферы 2, 3, 4. По принципу Гюйгенса парциальные волны гасят друг друга в результате интерференции всюду, за исключением их огибающей, которая образует в скважине коническую поверхность (линия 5 на рис. 3, а). Эта волновая поверхность представляет фронт волны
(окружности 1 на рис. 3, а и б). Аналогично волны, излученные из точек В, С, D, представляют сферы 2, 3, 4. По принципу Гюйгенса парциальные волны гасят друг друга в результате интерференции всюду, за исключением их огибающей, которая образует в скважине коническую поверхность (линия 5 на рис. 3, а). Эта волновая поверхность представляет фронт волны 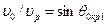 фронт перемещается под критическим углом к стенке скважины. Допустив, что скорость в породе меньше чем в жидкости, убеждаемся, что общая огибающая в этом случае не возникает и волна в жидкости не образуется (см. рис. 3, б).
фронт перемещается под критическим углом к стенке скважины. Допустив, что скорость в породе меньше чем в жидкости, убеждаемся, что общая огибающая в этом случае не возникает и волна в жидкости не образуется (см. рис. 3, б). , для которого
, для которого  , называют вторым критическим. При углах
, называют вторым критическим. При углах 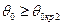 также имеет место полное внутреннее отражение, в связи, с чем в породе возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью
также имеет место полное внутреннее отражение, в связи, с чем в породе возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью  поперечной волны в породе. Условие образования головной волны в данном случае
поперечной волны в породе. Условие образования головной волны в данном случае 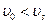 . Эта волна также образует продольную волну в жидкости, обозначаемую
. Эта волна также образует продольную волну в жидкости, обозначаемую 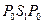 . Ее конический фронт перемещается вдоль оси скважины со скоростью
. Ее конический фронт перемещается вдоль оси скважины со скоростью 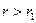 уменьшаются с увеличением r. Уменьшение амплитуд тем интенсивнее, чем больше угол
уменьшаются с увеличением r. Уменьшение амплитуд тем интенсивнее, чем больше угол 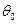 , при котором возникла головная волна. Поэтому коэффициент передачи энергии в головную волну максимален вблизи
, при котором возникла головная волна. Поэтому коэффициент передачи энергии в головную волну максимален вблизи 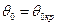 . Условно можно считать, что в кольцевом зазоре «прибор — стенка скважины» волна
. Условно можно считать, что в кольцевом зазоре «прибор — стенка скважины» волна  ), а дискретно в точках А, В, С и т. д. (см. рис. 2), расположенных, как нетрудно видеть, на расстоянии
), а дискретно в точках А, В, С и т. д. (см. рис. 2), расположенных, как нетрудно видеть, на расстоянии 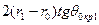 одна от другой. Интерференцией этих волн (их «пристраиванием» одна к другой) объясняется вид головной монотипной волны, регистрируемой в скважине. Действительно, форма головной волны должна, казалось бы, повторять форму излученного импульса, имеющего 1,5—2 периода. Однако ее реальная форма представляет собой цуг колебаний, число периодов в котором существенно больше.
одна от другой. Интерференцией этих волн (их «пристраиванием» одна к другой) объясняется вид головной монотипной волны, регистрируемой в скважине. Действительно, форма головной волны должна, казалось бы, повторять форму излученного импульса, имеющего 1,5—2 периода. Однако ее реальная форма представляет собой цуг колебаний, число периодов в котором существенно больше.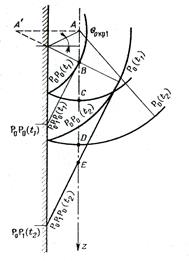 Время распространения волны
Время распространения волны 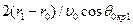 . Время прохождения волной
. Время прохождения волной  . Интерференция в фазе возникает, если разность этих времен кратна периоду. Отсюда, учитывая, что
. Интерференция в фазе возникает, если разность этих времен кратна периоду. Отсюда, учитывая, что 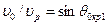 , получаем
, получаем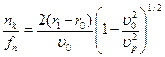
 Где
Где 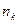 целое число,
целое число, 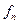 — частота волны, испытавшей конструктивную интерференцию. Видимая частота волны
— частота волны, испытавшей конструктивную интерференцию. Видимая частота волны 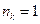 .
. а обменной —
а обменной —  , где
, где 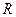 — расстояние, пройденное в породе. Если оно учтено, затухание можно считать функцией только параметров среды.
— расстояние, пройденное в породе. Если оно учтено, затухание можно считать функцией только параметров среды.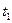 и
и  (рис. 4).
(рис. 4).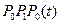 впервые достигла оси z скважины в точке В, расположенной на расстоянии
впервые достигла оси z скважины в точке В, расположенной на расстоянии 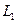 от источника излучения А. Одновременно с ней достиг точки В и фронт отраженной волны
от источника излучения А. Одновременно с ней достиг точки В и фронт отраженной волны 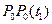 , который может быть построен с помощью мнимого источника А'. Прямая волна
, который может быть построен с помощью мнимого источника А'. Прямая волна 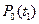 к этому моменту обгоняет фронт головной волны на величину отрезка ВС. Однако фронт волны
к этому моменту обгоняет фронт головной волны на величину отрезка ВС. Однако фронт волны 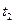 он обгоняет его на величину отрезка DЕ. Очевидно, что
он обгоняет его на величину отрезка DЕ. Очевидно, что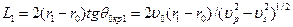 .
.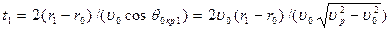 .
.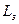 от источника
от источника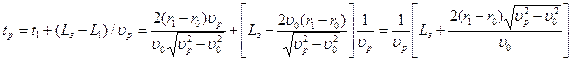 (3.9)
(3.9)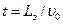 . (3.10)
. (3.10)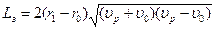 (3.11)
(3.11)


