
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Водные и поверхностные волны в скважинеСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Если индекс l =1, а индекс n = 0, выражение (2.4б) характеризует в частности водную волну
Рис 1. Механизм образования отражённых водных волн Фактически длительность импульса превышает время распространения волн от излучателя до стенки скважины, т.е. он существует в некотором интервале времени. Картина в этом интервале близка к той, какая была бы при непрерывной работе излучателя. В результате в зазоре возникает сложное интерференционное поле. Тем не менее, поскольку у реального импульса есть начало, первые вступления прямой волны не осложнены интерференцией с отраженными водными волнами. Из теории известно, что равенство нулю знаменателя коэффициента отражения А, входящего в выражение (2.42), свидетельствует о возникновении поверхностных волн. В данном случае их две — волна Лэмба и псевдорелеевская. При стремлении частоты к бесконечности стенка скважины становится как бы плоской и скорость волны Лэмба монотонно приближается к скорости поверхностной волны Стоунли, возникающей на плоской границе жидкости и твердого тела. Поэтому волну Лэмба иногда называют волной Лэмба — Стоунли. Возникновение волны Лэмба можно объяснить следующим образом. На низких частотах ( Если бы стенка скважины была абсолютно жесткой, смещения в рассматриваемой плоской волне были бы только продольными, а ее фазовая скорость равнялась скорости Поскольку радиальные смещения в волне Лэмба невелики, рассеяние энергии в породу минимально и волна распространяется на большие расстояния вдоль оси z с малым затуханием. Картина меняется, если пласт проницаем. Расхождение фронта и фильтрация жидкости из областей сгущения в пласт и из пласта в области разряжения, соответствующие возникновению продольной волны второго рода, приводит к заметному снижению амплитуды волны Лэмба. На этом явлении основано выделение проницаемых пластов. Наряду с волной Лэмба в скважине образуется поверхностная волна релеевского типа. Поскольку в рассматриваемом случае твердая среда контактирует с жидкостью, а не с воздухом, как в наземной сейсморазведке, это псевдорелеевская волна. Ее скорость, как и у обычной релеевской волны, близка к скорости Основное практическое значение среди рассмотренных выше волн имеет волна Лэмба. Найдем выражение для ее скорости, считая для простоты, что прибора в скважине нет. Смещение частиц в волне Лэмба, как уже говорилось, направлено главным образом вдоль оси z и может рассматриваться как функция Движение в осевом направлении обусловлено градиентом давления вдоль оси z, что можно выразить количественно, приравнивая действующую в этом направлении силу к массе, умноженной на ускорение для элементарной цилиндрической области длиной
где
По мере роста давления, объем
или, в соответствии с формулой (1.7),
Г. Лэмб (1960 г.) показал, что для рассматриваемых условий
где
Выполнив дифференцирование по z, получим:
С учетом (3.1), выражение (3.4) можно записать как
Сравнивая выражения (3.5) и (2.5), видим, что полученное волновое уравнение характеризует волну, распространяющуюся вдоль скважины со скоростью
Преобразовав (3.6), с учетом (2.7), получим:
Итак, скорость волны Лэмба несколько меньше скорости продольной волны в скважинной жидкости. Измерив С помощью формул (2.7) и (2.17) уравнение (3.7) преобразуется к виду:
из чего следует, что, измерив скорости Головные волны в скважине
Угол Поскольку в волне Головные волны Вследствие интерференции распределение энергии в спектре зарегистрированных колебаний отличается от ее распределения в спектре излученных колебаний. Подчеркиваются те частоты, для которых интерференция происходит в фазе, иными словами, для которых на участках ADB, ВЕС (см. рис. 2) укладывается целое число волн. Это явление называют конструктивной интерференцией. Поскольку отрезок АD для волны В общем случае видимая частота соответствует наименьшей частоте конструктивной интерференции. Определим ее.
Видимую частоту волны В реальных условиях диаметр скважины меняется, а прибор отклоняется от оси. Поэтому распределение энергии в спектре зарегистрированных колебаний, в известной степени, случайная величина и спектральный анализ сигналов с целью определения параметров пород целесообразно проводить по начальной части волновой картины, которая не осложнена конструктивной интерференцией. При распространении головных волн вдоль стенки скважины они затухают за счет расхождения и поглощения. На низких частотах расхождение монотипной волны пропорционально Интерференция волн затрудняет, а иногда делает невозможной их идентификацию. Рассмотрим в лучевом приближении положение фронтов прямых Допустим в момент времени t = 0 излучен импульс упругих колебаний, а в момент
Время прихода волны
Время прихода головной волны в точку, расположенную на расстоянии длины зонда
Зависимость времени прихода волны от расстояния
Сопоставление выражений (3.9) и (3.10) показывает, что при
монотипная волна обгоняет прямую. Аналогично можно найти годограф обменной волны и определить расстояние, при котором ее удастся зарегистрировать раньше, чем возникнет интерференция с прямой волной. Таким образом, существует принципиальная возможность регистрации не осложненных интерференцией головных волн в скважине. Их параметры характеризуют упругие свойства среды за стенкой скважины.
|
||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 561; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

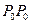 , возникшую в результате первого отражения прямой водной волны
, возникшую в результате первого отражения прямой водной волны 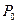 от стенки.
от стенки. При последующих отражениях в каждой точке кольцевого зазора между стенкой скважины и прибором последовательно образуются отраженные водные волны
При последующих отражениях в каждой точке кольцевого зазора между стенкой скважины и прибором последовательно образуются отраженные водные волны  (n =1, l =2);
(n =1, l =2); 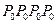 (n =2, l =3); и т.д., амплитуды которых при
(n =2, l =3); и т.д., амплитуды которых при 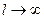 стремятся к нулю. Поскольку путь АВС (рис. 1) больше пути АС, а скорости водных волн равны, при мгновенном импульсе излучения прямые и отраженные волны не интерферируют.
стремятся к нулю. Поскольку путь АВС (рис. 1) больше пути АС, а скорости водных волн равны, при мгновенном импульсе излучения прямые и отраженные волны не интерферируют.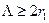 ) скважину можно рассматривать как узкую трубу, обладающую, в общем случае, следующим свойством: какой бы излучатель не создавал в ней гармоническое акустическое поле, на некотором расстоянии от излучателя будет распространяться одномерная (параметры зависят только от z и t) волна с плоским фронтом, практически перпендикулярным к стенке трубы.
) скважину можно рассматривать как узкую трубу, обладающую, в общем случае, следующим свойством: какой бы излучатель не создавал в ней гармоническое акустическое поле, на некотором расстоянии от излучателя будет распространяться одномерная (параметры зависят только от z и t) волна с плоским фронтом, практически перпендикулярным к стенке трубы.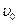 упругих волн в свободной жидкости. Фактически порода сжимаема, в связи, с чем наличие в жидкости областей повышенного и пониженного давления вызывает небольшие радиальные смещения стенок, и столб жидкости дополнительно укорачивается или растягивается. Это явление эквивалентно увеличению сжимаемости среды, и скорость волны оказывается несколько меньше
упругих волн в свободной жидкости. Фактически порода сжимаема, в связи, с чем наличие в жидкости областей повышенного и пониженного давления вызывает небольшие радиальные смещения стенок, и столб жидкости дополнительно укорачивается или растягивается. Это явление эквивалентно увеличению сжимаемости среды, и скорость волны оказывается несколько меньше  поперечной волны в породе, но при распространении она непрерывно излучает энергию в жидкость и быстро затухает. Поэтому ее трудно обнаружить на фоне обменной головной волны, скорость которой, как будет показано ниже, равна
поперечной волны в породе, но при распространении она непрерывно излучает энергию в жидкость и быстро затухает. Поэтому ее трудно обнаружить на фоне обменной головной волны, скорость которой, как будет показано ниже, равна 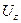 координаты z и времени t. Радиальные смещения стенки скважины
координаты z и времени t. Радиальные смещения стенки скважины  ,- незначительны.
,- незначительны.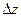 :
:
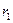 — радиус скважины. Отсюда
— радиус скважины. Отсюда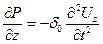 . (3.1)
. (3.1) элементарной цилиндрической области изменяется. Его изменение
элементарной цилиндрической области изменяется. Его изменение 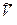 состоит из двух частей:
состоит из двух частей:  , обусловленной осевым движением, и
, обусловленной осевым движением, и 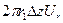 , обусловленной радиальным расширением стенки скважины. Деление суммы этих частей на объем
, обусловленной радиальным расширением стенки скважины. Деление суммы этих частей на объем 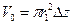 дает
дает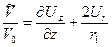
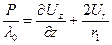 (3.2)
(3.2)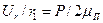 , (3.3)
, (3.3)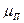 — константа Ламэ (сдвиговая жесткость породы). В результате, выражение (3.2) принимает вид:
— константа Ламэ (сдвиговая жесткость породы). В результате, выражение (3.2) принимает вид: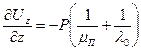
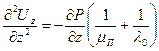 (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) . (3.7)
. (3.7)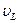 и зная параметры скважинной жидкости
и зная параметры скважинной жидкости  , определяют
, определяют  (3.8)
(3.8)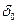 , можно определить плотность породы
, можно определить плотность породы 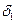 .
.
 Наряду с отраженной волной
Наряду с отраженной волной  (рис. 2). Направления их волновых векторов связаны законом Снеллиуса, являющимся выражением принципа причинности, который в данном случае можно сформулировать как условие неразрывности фронтов отраженной и преломленной волн. На основе простых геометрических построений не трудно показать, что если это условие выполняется,
(рис. 2). Направления их волновых векторов связаны законом Снеллиуса, являющимся выражением принципа причинности, который в данном случае можно сформулировать как условие неразрывности фронтов отраженной и преломленной волн. На основе простых геометрических построений не трудно показать, что если это условие выполняется, 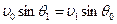 . Угол
. Угол 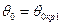 для которого
для которого 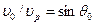 (соответственно
(соответственно 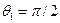 ), называют первым критическим. При углах падения
), называют первым критическим. При углах падения  имеет место полное внутреннее отражение, в связи, с чем возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью
имеет место полное внутреннее отражение, в связи, с чем возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью 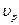 продольной волны в породе. Учитывая механизм образования, их, как и преломленные, обозначают
продольной волны в породе. Учитывая механизм образования, их, как и преломленные, обозначают 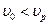 .
.
 Поскольку скорость головной волны
Поскольку скорость головной волны 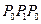 . Механизм ее образования можно пояснить на основе принципа Гюйгенса — Френеля. Для этого каждую точку стенки скважины, например A, В, С, D (рис. 3), следует считать источником волны
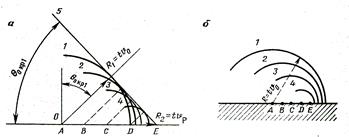
. Механизм ее образования можно пояснить на основе принципа Гюйгенса — Френеля. Для этого каждую точку стенки скважины, например A, В, С, D (рис. 3), следует считать источником волны 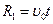 (окружности 1 на рис. 3, а и б). Аналогично волны, излученные из точек В, С, D, представляют сферы 2, 3, 4. По принципу Гюйгенса парциальные волны гасят друг друга в результате интерференции всюду, за исключением их огибающей, которая образует в скважине коническую поверхность (линия 5 на рис. 3, а). Эта волновая поверхность представляет фронт волны
(окружности 1 на рис. 3, а и б). Аналогично волны, излученные из точек В, С, D, представляют сферы 2, 3, 4. По принципу Гюйгенса парциальные волны гасят друг друга в результате интерференции всюду, за исключением их огибающей, которая образует в скважине коническую поверхность (линия 5 на рис. 3, а). Эта волновая поверхность представляет фронт волны 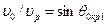 фронт перемещается под критическим углом к стенке скважины. Допустив, что скорость в породе меньше чем в жидкости, убеждаемся, что общая огибающая в этом случае не возникает и волна в жидкости не образуется (см. рис. 3, б).
фронт перемещается под критическим углом к стенке скважины. Допустив, что скорость в породе меньше чем в жидкости, убеждаемся, что общая огибающая в этом случае не возникает и волна в жидкости не образуется (см. рис. 3, б). , для которого
, для которого  , называют вторым критическим. При углах
, называют вторым критическим. При углах 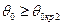 также имеет место полное внутреннее отражение, в связи, с чем в породе возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью
также имеет место полное внутреннее отражение, в связи, с чем в породе возникают головные волны, распространяющиеся вдоль границы твердой и жидкой фаз со скоростью 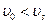 . Эта волна также образует продольную волну в жидкости, обозначаемую
. Эта волна также образует продольную волну в жидкости, обозначаемую 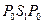 . Ее конический фронт перемещается вдоль оси скважины со скоростью
. Ее конический фронт перемещается вдоль оси скважины со скоростью 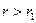 уменьшаются с увеличением r. Уменьшение амплитуд тем интенсивнее, чем больше угол
уменьшаются с увеличением r. Уменьшение амплитуд тем интенсивнее, чем больше угол 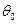 , при котором возникла головная волна. Поэтому коэффициент передачи энергии в головную волну максимален вблизи
, при котором возникла головная волна. Поэтому коэффициент передачи энергии в головную волну максимален вблизи 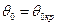 . Условно можно считать, что в кольцевом зазоре «прибор — стенка скважины» волна
. Условно можно считать, что в кольцевом зазоре «прибор — стенка скважины» волна  ), а дискретно в точках А, В, С и т. д. (см. рис. 2), расположенных, как нетрудно видеть, на расстоянии
), а дискретно в точках А, В, С и т. д. (см. рис. 2), расположенных, как нетрудно видеть, на расстоянии 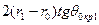 одна от другой. Интерференцией этих волн (их «пристраиванием» одна к другой) объясняется вид головной монотипной волны, регистрируемой в скважине. Действительно, форма головной волны должна, казалось бы, повторять форму излученного импульса, имеющего 1,5—2 периода. Однако ее реальная форма представляет собой цуг колебаний, число периодов в котором существенно больше.
одна от другой. Интерференцией этих волн (их «пристраиванием» одна к другой) объясняется вид головной монотипной волны, регистрируемой в скважине. Действительно, форма головной волны должна, казалось бы, повторять форму излученного импульса, имеющего 1,5—2 периода. Однако ее реальная форма представляет собой цуг колебаний, число периодов в котором существенно больше.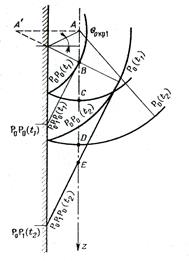 Время распространения волны
Время распространения волны 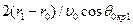 . Время прохождения волной
. Время прохождения волной  . Интерференция в фазе возникает, если разность этих времен кратна периоду. Отсюда, учитывая, что
. Интерференция в фазе возникает, если разность этих времен кратна периоду. Отсюда, учитывая, что 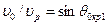 , получаем
, получаем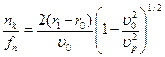
 Где
Где 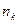 целое число,
целое число, 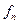 — частота волны, испытавшей конструктивную интерференцию. Видимая частота волны
— частота волны, испытавшей конструктивную интерференцию. Видимая частота волны 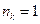 .
. а обменной —
а обменной —  , где
, где 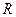 — расстояние, пройденное в породе. Если оно учтено, затухание можно считать функцией только параметров среды.
— расстояние, пройденное в породе. Если оно учтено, затухание можно считать функцией только параметров среды.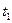 и
и  (рис. 4).
(рис. 4).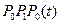 впервые достигла оси z скважины в точке В, расположенной на расстоянии
впервые достигла оси z скважины в точке В, расположенной на расстоянии 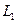 от источника излучения А. Одновременно с ней достиг точки В и фронт отраженной волны
от источника излучения А. Одновременно с ней достиг точки В и фронт отраженной волны 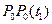 , который может быть построен с помощью мнимого источника А'. Прямая волна
, который может быть построен с помощью мнимого источника А'. Прямая волна 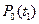 к этому моменту обгоняет фронт головной волны на величину отрезка ВС. Однако фронт волны
к этому моменту обгоняет фронт головной волны на величину отрезка ВС. Однако фронт волны 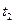 он обгоняет его на величину отрезка DЕ. Очевидно, что
он обгоняет его на величину отрезка DЕ. Очевидно, что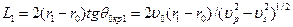 .
.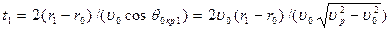 .
.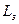 от источника
от источника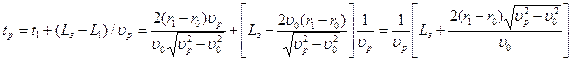 (3.9)
(3.9)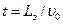 . (3.10)
. (3.10)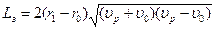 (3.11)
(3.11)


