
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Методы решения прямой задачи скважинной акустикиСодержание книги Поиск на нашем сайте
Выше рассмотрены акустические свойства безграничных изотропных сред. Появление цилиндрических границ, обусловленных наличием скважины и скважинного прибора, меняет условия распространения акустических волн. Особенно существенно их влияние на параметры волн, распространяющихся в скважине и в непосредственной близости от нее. Распространение упругих волн в среде со скважиной и скважинным прибором описывается решением краевой задачи для волнового уравнения вида (2.5) с ненулевой правой частью, выражающей функцию источника. Аналитически это уравнение в общем случае не решается. Для конкретных условий его интегрирование осуществляют численными методами. Обычно применяют метод конечных разностей и операторный. В ряде случаев волновое поле в скважине исследуют методами натурного моделирования. Метод конечных разностей применяют при комбинации плоских и цилиндрических границ раздела. Подобно тому, как это делалось при решении прямой задачи электрического каротажа, производные, входящие в волновое уравнение, заменяют их разностными аппроксимациями так, что в узлах сетки, дискретизирующей пространство, значения непрерывной и дискретной функций (потенциала, давления, смещения) совпадают. В результате волновое уравнение второй степени в частных производных сводят к системе алгебраических уравнений. Однако конечно-разностные методы имеют серьезные недостатки. Основной из них в том, что полученное решение характеризует волновой процесс в целом, в связи, с чем нельзя корректно выделить составляющие его волны и оценить их параметры. Операторный метод позволяет в принципе определить типы возникающих в скважине волн и оценить параметры каждой из них. Суть метода в том, что от дифференциальных уравнений в частных производных к обыкновенным дифференциальным уравнениям переходят посредством ряда интегральных преобразований. После решения алгебраического уравнения, с помощью обратных преобразований получают решение исходного дифференциального уравнения. Операторный метод эффективен для относительно простых моделей, например для случая скважины, пересекающей пласт бесконечной мощности с осесимметрично расположенным скважинным прибором, а также в случае упрощающих (асимптотических) приближений. Натурное моделирование позволяет изучить условия образования и распространения волн для сложных моделей среды. К таким моделям в первую очередь следует отнести комбинацию цилиндрических границ, имитирующих обсаженную скважину, а также комбинацию цилиндрических и горизонтальных границ. Кроме того, натурное моделирование дает возможность учесть реальные характеристики акустических излучателей, приемников, изоляторов и оценить, таким образом, эффективность их конструкции. Особую трудность при натурном моделировании представляет подбор материалов. Обычно их готовят на основе эпоксидных смол и специально подобранных наполнителей. Обсаженные скважины имитируют, используя стальные, пластмассовые, стеклянные трубки. В ряде случаев обеспечивают возможность изменения давления и температуры. С помощью перечисленных методов изучены основные закономерности пространственно-временного распределения волнового поля в открытых и обсаженных скважинах. Применение операторного метода рассмотрим на примере решения следующей задачи. Скважинный прибор радиуса Отметим, что задача с δ-импульсом наиболее общая. Для источника, генерирующего колебания, описываемые произвольной функцией F(t), вид поля f(t) связан с полем Р(t) интегралом свертки
С учетом вышеперечисленных условий и формулы (2.7) уравнение (2.5) для давления в скважине примет вид:
где П — константа, обеспечивающая необходимую размерность и имеющая модуль, равный единице, а 1/2πR — множитель, позволяющий перейти к плотности кольцевого источника. Преобразуем уравнение (2.36) для условий осевой симметрии следующим образом:
Для среды вне скважины, где источник отсутствует, применимы аналогичные уравнения с нулевой правой частью. Поскольку эта среда твердая, запишем их для скалярного φ и векторного Уравнение для скалярного потенциала:
При выводе волнового уравнения для векторного потенциала учтем, что в данном случае div
Волновое уравнение для векторного потенциала с учетом выражения (2.39):
В систему уравнений (2.37), (2.38), (2.40) входят производные по r, z, t. Применив преобразование Фурье сначала по t, а затем по z, получим систему обыкновенных дифференциальных уравнений с производными только по r:
Обыкновенные дифференциальные уравнения, входящие в систему (2.41) — уравнения Бесселя. Из теории известно, что решение первого из них, удовлетворяющее условию конечности поля на стенке прибора (при r→
где Наличие трех слагаемых в квадратных скобках связано с существованием в зазоре «стенка скважины — прибор» трех типов волн: приходящей — отразившейся от стенки скважины, и двух уходящих — прямой и отразившейся от стенки прибора. Поскольку при r→∞ функция
где Равенства (2.42) и (2.43) содержат четыре неизвестных коэффициента: А, В, С, D. Для их нахождения необходимо воспользоваться четырьмя условиями сопряжения, выраженными через Согласно выражению (1.7)
Волновое уравнение для скалярного потенциала
Отсюда с учётом формулы (2.7)
Образ функции
Сформулируем условия сопряжения. Поскольку первая среда — стенка прибора — абсолютно жесткая, условия сопряжения на границе с ней выражаются в равенстве нулю нормальных смещений (первое условие сопряжения). Для границы скважинная жидкость — пласт условия сопряжения выражаются в равенстве нормальных смещений (второе условие), равенстве нормальных напряжений (третье условие) и, поскольку одна среда жидкая — равенстве нулю касательных напряжений (четвертое условие). Согласно условию задачи, определению подлежит поле акустического давления в скважине. Его находят с помощью обратного преобразования Фурье для выражения (2.42), используя найденные значения коэффициентов А и В. Полученный в результате интеграл содержит специальные функции и не имеет в общем случае аналитического решения. Условно решение можно представить в виде
где член
|
||||
|
Последнее изменение этой страницы: 2016-09-17; просмотров: 349; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.142.198.250 (0.011 с.) |

 и бесконечной длины с абсолютно жестким корпусом — последнее условие означает, что амплитуда распространяющейся по нему волны стремится к нулю, расположен на оси скважины радиусом
и бесконечной длины с абсолютно жестким корпусом — последнее условие означает, что амплитуда распространяющейся по нему волны стремится к нулю, расположен на оси скважины радиусом 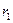 , заполненной идеальной жидкостью, скорость продольной волны в которой
, заполненной идеальной жидкостью, скорость продольной волны в которой 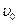 , а плотность
, а плотность 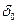 . Скважина пересекает изотропный пласт бесконечной мощности, представленный однофазной (К — действительное число) породой, скорости продольной и поперечной волн в которой
. Скважина пересекает изотропный пласт бесконечной мощности, представленный однофазной (К — действительное число) породой, скорости продольной и поперечной волн в которой 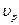 и
и  а плотность
а плотность  . На корпусе прибора расположены кольцевой излучатель и приемники (кольцом считаем цилиндр, высота которого стремится к нулю). В момент времени t = 0, на бесконечно близком расстоянии от стенки прибора возник мгновенный импульс акустического давления (δ - импульс) в виде кольца радиусом R. Задача заключается в нахождении полного поля акустического давления Р(t) в любой точке внутри скважины.
. На корпусе прибора расположены кольцевой излучатель и приемники (кольцом считаем цилиндр, высота которого стремится к нулю). В момент времени t = 0, на бесконечно близком расстоянии от стенки прибора возник мгновенный импульс акустического давления (δ - импульс) в виде кольца радиусом R. Задача заключается в нахождении полного поля акустического давления Р(t) в любой точке внутри скважины.
 , (2.36)
, (2.36) (2.37)
(2.37) потенциалов.
потенциалов. (2.38)
(2.38) - компонента векторного потенциала, т. е. ψ =
- компонента векторного потенциала, т. е. ψ =  . (2.39)
. (2.39)


 (2.41)
(2.41)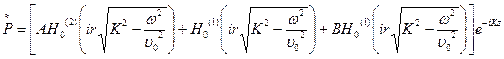 (2.42)
(2.42) ,
,  - функции Ханкеля нулевого порядка второго и первого рода, соответственно, от мнимого аргумента
- функции Ханкеля нулевого порядка второго и первого рода, соответственно, от мнимого аргумента  .
. убывает, первое слагаемое характеризует приходящую волну, а два других — уходящие. Соответственно множитель А является коэффициентом отражения от стенки скважины, а множитель В — от стенки прибора. Решения уравнений (2.41б) и (2.41в), удовлетворяющие условиям затухания излучения на бесконечности, имеют вид:
убывает, первое слагаемое характеризует приходящую волну, а два других — уходящие. Соответственно множитель А является коэффициентом отражения от стенки скважины, а множитель В — от стенки прибора. Решения уравнений (2.41б) и (2.41в), удовлетворяющие условиям затухания излучения на бесконечности, имеют вид:
 (2.43)
(2.43)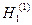 — функция Ханкеля первого порядка первого рода, С и D — постоянные коэффициенты.
— функция Ханкеля первого порядка первого рода, С и D — постоянные коэффициенты. ,
,  и
и  . Выразим через образ потенциала
. Выразим через образ потенциала 
 при
при  можно записать с нулевой правой частью:
можно записать с нулевой правой частью: .
. (2.44)
(2.44) — функция
— функция  .Поэтому
.Поэтому . (2.45)
. (2.45) (2.44)
(2.44) характеризует прямую водную волну, а члены ряда — отраженные волны, под которыми следует понимать отраженные водные волны, а также волны поверхностные и головные. Каждый член ряда описывает регистрируемое кольцевым приемником акустическое поле, созданное волнами всех названных типов, l раз отразившихся от стенки скважины и n — от стенки прибора, и являющееся функцией времени t, координаты кольцевого приемника z и его радиуса r. Сумма ряда описывает суммарное поле, регистрируемое после l -, n - отражений. В принципе эта сумма распадается на две, одна из которых соответствует отраженным волнам, распространяющимся от прибора (n = l) а другая — отраженным волнам, распространяющимся к прибору (n = l -1). Поскольку радиус приемника
характеризует прямую водную волну, а члены ряда — отраженные волны, под которыми следует понимать отраженные водные волны, а также волны поверхностные и головные. Каждый член ряда описывает регистрируемое кольцевым приемником акустическое поле, созданное волнами всех названных типов, l раз отразившихся от стенки скважины и n — от стенки прибора, и являющееся функцией времени t, координаты кольцевого приемника z и его радиуса r. Сумма ряда описывает суммарное поле, регистрируемое после l -, n - отражений. В принципе эта сумма распадается на две, одна из которых соответствует отраженным волнам, распространяющимся от прибора (n = l) а другая — отраженным волнам, распространяющимся к прибору (n = l -1). Поскольку радиус приемника  , волны, распространяющиеся от прибора, им не регистрируются
, волны, распространяющиеся от прибора, им не регистрируются


