
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Дисперсия света. Наблюдение. Аномальная и нормальная. Графики. Понятие групповой скорости. Вывод формулы для групповой скорости.Содержание книги
Поиск на нашем сайте Дисперсией света называется зависимость показателя преломления n вещества от частоты ν(длины волн λ) света или зависимость фазовой скорости световых волн от их частоты. Дисперсия света представляется в виде зависимости:
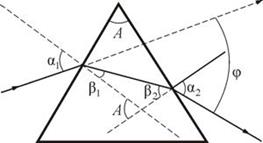
Следствием дисперсии является разложение в спектр пучка белого света при прохождении его через призму (рис. 10.1). Первые экспериментальные наблюдения дисперсии света проводил в 1672 г. И. Ньютон. Он объяснил это явление различием масс корпускул.
Пучок белого света за призмой разлагается в спектр, который называется дисперсионным или призматическим. Таким образом, с помощью призмы, так же как с помощью дифракционной решетки, разлагая свет в спектр, можно определить его спектральный состав. Рассмотрим различия в дифракционном и призматическом спектрах. · Дифракционная решетка разлагает свет непосредственно по длинам волн, поэтому по измеренным углам (по направлениям соответствующих максимумов) можно вычислить длину волны (частоты). Разложение света в спектр в призме происходит по значениям показателя преломления, поэтому для определения частоты или длины волны света надо знать зависимость · Составные цвета в дифракционном и призматическом спектрах располагаются различно. Мы знаем, что синус угла в дифракционной решетке пропорционален длине волны Величина
Из рис. выше следует, что показатель преломления для прозрачных веществ с увеличением длины волны увеличивается, следовательно величина Области значения ν, в которых
соответствуют нормальной дисперсии света (с ростом частоты ν показатель преломления n увеличивается). Нормальная дисперсия наблюдается у веществ, прозрачных для света. Например, обычное стекло прозрачно для видимого света, и в этой области частот наблюдается нормальная дисперсия света в стекле. На основе явления нормальной дисперсии основано «разложение» света стеклянной призмой монохроматоров. Дисперсия называется аномальной, если
т.е. с ростом частоты ν показатель преломления n уменьшается. Аномальная дисперсия наблюдается в областях частот, соответствующих полосам интенсивного поглощения света в данной среде. Например, у обычного стекла в инфракрасной и ультрафиолетовой частях спектра наблюдается аномальная дисперсия.
Зависимости n от ν и λ показаны на рис. выше В зависимости от характера дисперсии групповая скорость u в веществе может быть как больше, так и меньше фазовой скорости υ (в недиспергирующей среде Групповая скорость u связана с циклической частотой ω и волновым числом k соотношением:
Отсюда можно записать:
Таким образом, при нормальной дисперсии u < υ и При аномальной дисперсии u > υ, и, в частности, если
|
||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 582; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 или
или 
 . Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи света в спектре по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны (т.е. с уменьшением частоты) уменьшается.
. Следовательно, красные лучи, имеющие большую длину волны, чем фиолетовые, отклоняются дифракционной решеткой сильнее. Призма же разлагает лучи света в спектре по значениям показателя преломления, который для всех прозрачных веществ с увеличением длины волны (т.е. с уменьшением частоты) уменьшается. (или
(или  ), называемая дисперсией вещества, показывает, как быстро меняется показатель преломления с длиной волны.
), называемая дисперсией вещества, показывает, как быстро меняется показатель преломления с длиной волны.
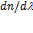 по модулю также увеличивается с уменьшением λ. Такая дисперсия называется нормальной. Вблизи линий и полос поглощения, ход кривой дисперсии
по модулю также увеличивается с уменьшением λ. Такая дисперсия называется нормальной. Вблизи линий и полос поглощения, ход кривой дисперсии  будет иным, а именно n уменьшается с уменьшением λ. Такой ход зависимости n от λ называется аномальной дисперсией.
будет иным, а именно n уменьшается с уменьшением λ. Такой ход зависимости n от λ называется аномальной дисперсией. (или
(или  )
)
 (или
(или 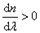 ),
),

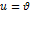 ).
). , где
, где  ,
,  . Тогда
. Тогда .
.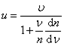 .
.
 , то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.
, то u > c. Этот результат не противоречит специальной теории относительности. Понятие групповой скорости правильно описывает распространение только такого сигнала (волнового пакета), форма которого не изменяется при перемещении сигнала в среде. (Строго говоря, это условие выполняется только для вакуума, т.е. в недиспергирующей среде). В области частот, соответствующих аномальной дисперсии, групповая скорость не совпадает со скоростью сигнала, так как вследствие значительной дисперсии форма сигнала так быстро изменяется, что не имеет смысла говорить о групповой скорости.


