
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Уравнение Эйнштейна для фотоэффекта и экспериментальные методы его проверки.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данное уравнение называется уравнением Эйнштейна для внешнего фотоэффекта. На основе этих соображений, фотонная (корпускулярная) теория света предсказывает следующее. 1. Увеличение интенсивности света означает увеличение числа налетающих фотонов, которые выбивают с поверхности металла больше электронов. Но так как энергия фотонов одна и та же, максимальная кинетическая энергия электрона не изменится (подтверждается I закон фотоэффекта). 2. При увеличении частоты падающего света максимальная кинетическая энергия электронов линейно возрастает в соответствии с формулой Эйнштейна. (Подтверждение II закона фотоэффекта). График этой зависимости представлен на рис.
3. Если частота ν меньше критической частоты Уравнение Эйнштейна было подтверждено опытами Милликена, выполненными в 1913–1914 гг. Основное отличие от опыта Столетова в том, что поверхность металла подвергалась очистке в вакууме. Исследовалась зависимость максимальной кинетической энергии от частоты и определялась постоянная Планка h. В 1926 г. российские физики П.И. Лукирский и С.С. Прилежаев для исследования фотоэффекта применили метод вакуумного сферического конденсатора. Анодом служили посеребренные стенки стеклянного сферического баллона, а катодом – шарик (R ≈ 1,5 см) из исследуемого металла, помещенного в центр сферы. Такая форма электродов позволяла увеличить наклон ВАХ и тем самым более точно определить задерживающее напряжение (а следовательно, и h). Значение постоянной Планка h, полученное из этих опытов, согласуется со значениями, найденными другими методами (по излучению черного тела и по коротковолновой границе сплошного рентгеновского спектра). Все это является доказательством правильности уравнения Эйнштейна, а вместе с тем и его квантовой теории фотоэффекта. Наиболее непосредственное подтверждение гипотезы Эйнштейна дал опыт Боте, в котором использовался метод совпадения
Тонкая металлическая фольга Ф помещалась между двумя газоразрядными счетчиками Сч. Фольга освещалась слабым пучком рентгеновских лучей, под действием которых она сама становилась источником рентгеновских лучей (это явление называется рентгеновской флуоресценцией). Вследствие малой интенсивности первичного пучка, количество квантов, испускаемых фольгой, было невелико. При попадании квантов на счетчик механизм срабатывал и на движущейся бумажной ленте делалась отметка. Если бы излучаемая энергия распространялась равномерно во все стороны, как это следует из волновых представлений, оба счетчика должны были срабатывать одновременно и отметки на ленте приходились бы одна против другой. В действительности же наблюдалось совершенно беспорядочное расположение отметок. Это можно объяснить лишь тем, что в отдельных актах испускания возникают световые частицы, летящие то в одном, то в другом направлении.
Энергия, импульс, масса фотонов Фотон обладает энергией Фотон обладает инертной массой, которую можно найти из соотношения
Фотон движется со скоростью света c = 3·108 м/с. Подставим это значение скорости в выражение для релятивистской массы:
Фотон – частица, не обладающая массой покоя. Она может существовать, только двигаясь со скоростью света c.
Импульс фотона:
Эффект Комптона.
Частота рассеянного света меньше частоты падающего света Разность
где l’ – длина волны рассеянного излучения, 20. Корпускулярно-волновой дуализм материи и его опытное обоснование. Гипотеза де Бройля. Дифракция электронов и нейтронов (опыты по дифракции электронов).
|
||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-01; просмотров: 590; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.009 с.) |



 , то выбивание электронов с поверхности не происходит (III закон).
, то выбивание электронов с поверхности не происходит (III закон).
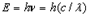 . Для видимого света длина волны λ = 0,5 мкм и энергия Е = 2,2 эВ, для рентгеновских лучей λ = мкм и Е = 0,5 эВ.
. Для видимого света длина волны λ = 0,5 мкм и энергия Е = 2,2 эВ, для рентгеновских лучей λ = мкм и Е = 0,5 эВ. :
: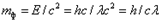 ;
;

 .
.
 или
или 

 не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния j:
не зависит от длины волны l падающего излучения и природы рассеивающего вещества, а определяется только углом рассеяния j:
 – комптоновская длина волны (при рассеянии фотона на электроне
– комптоновская длина волны (при рассеянии фотона на электроне  ).
).


