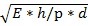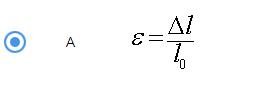Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
В в кууме мех ническое волны не могут р спростр нятьсяСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пр вильные: В продольной волне направление колебания частиц совпадает с направлением распространения волны При увеличении частоты колебаний интенсивность волны увеличивается Неправильные: Фронт волны - это множество точек, имеющих одинаковую амплитуду колебаний в определенный момент времени Механические волны могут распространяться в вакууме
Укажите формулу соотношения циклической частоты и периода колебаний: Скорость звука в твердом теле vп, как правило, больше скорости звука в жидкости vж, которая, в свою очередь, превышает скорость звука в газе vг. Совокупность гармонических колебаний, на которые разложено сложное колебание, называется... гармоническим спектром сложного колебания Правильные Уравнение волны устанавливает зависимость смещения колеблющейся точки, участвующей в волновом процессе, от координаты ее равновесного положения и времени Скорость распространения механических волн в твердых телах больше чем в жидкостях Неправильные При увеличении частоты колебаний интенсивность волны уменьшается В поперечной волне направление колебания частиц совпадает с направлением распространения волны Вынужденные колебания осуществляются за счет... воздействия периодически изменяющейся внешней силы Период колебаний обр тно пропорцион лен частоте колебаний Неправильные Коэффициент затухания колебаний не зависит от коэффициента трения Собственными, или свободными называются колебания, которые совершаются за счет изменяющейся внешней силы Величина, равная произведению плотности среды и скорости распространения механической волны называется волновым сопротивлением среды Метод доплерографии, применяемый в медицине, основан на измерении доплеровского сдвига частоты ультразвуковых волн Правильные Энергия, переносимая волной складывается из потенциальной энергии деформации и кинетической энергии колеблющихся частиц Укажите, какие из перечисленных колебаний являются гармоническими: свободные незатухающие Правильные Собственными, или свободными называются колебания, которые совершаются за счет первоначально накопленной в системе энергии Амплитуда свободных незатухающих колебаний не изменяется во времени Неправильные Явление резонанса наблюдается в системе, совершающей свободные колебания Собственными, или свободными называются колебания, которые совершаются при отсутствии силы трения Длина волны равна: наименьшему расстоянию между точками среды, фаза колебаний которых одинакова Вынужденные колебания – гармонические Сложные – негармонические При сближении источника и наблюдателя частота принимаемой волны больше частоты волны излучаемой источником Правильные Свободные незатухающие колебания являются гармоническими При увеличении частоты колебаний их период уменьшается НЕПРАВИЛЬНЫЕ Энергия колебательной системы не зависит от частоты колебаний Вынужденными называются колебания, которые совершаются под действием периодической внешней силы
БИОМЕМБРАНЫ 132 «Б» 2015 г. При выполнимости нормального закона распределения среднее значение осмотической устойчивости соответствует концентрации соли, при которой половина эритроцитов в суспензии лизировала, и половина не лизировала В целом, мембрана вместе с омывающими ее водными солевыми растворами может рассматриваться как электрический конденсатор, токопроводящими обкладками которого являются: водные растворы солей (диэлектрик – липидный слой) «Флип-флоп» диффузией молекул липидов в мембранах называется перескок молекул поперек мембраны из одного монослоя в другой Уравнение Нернста – Планка показывает, что перенос ионов определяется неравномерностью их распределения (градиентом концентрации) и воздействием электрического поля (градиентом электрического потенциала) Основу структуры биологических мембран составляют: двойной слой фосфолипидов Для возникновения трансмембранной разности потенциалов необходимо и достаточно: наличие избирательной проницаемости и различие концентраций ионов по обе стороны от мембраны Диффузию незаряженных частиц через мембраны описывает уравнение: J=-D(dc/dx) или J=P(c1-c2) Латеральной диффузией молекул в мембранах называется перемещение молекул вдоль плоскости мембраны Явление разрыва мембраны эритроцита, сопровождающееся выходом гемоглобина в окружающую среду называется гемолизом Плотностью потока вещества называют величину, равную числу молей молекул вещества, переносимых через единичную поверхность за единицу времени Простая диффузия происходит путем: растворения диффундирующего вещества в веществе мембраны При помещении эритроцитов в гипотонический раствор происходит увеличение объема клетки Вязкость липидного слоя мембран близка к вязкости: растительного масла Причиной возникновения осмотического гемолиза является диффузия через мембрану молекул воды из окружающего гипотонического раствора внутрь клетки В целом, мембрана вместе с омывающими ее водными солевыми растворами может рассматриваться как электрический конденсатор, диэлектриком которого является: только липиды мембраны Головки фосфолипидов биологических мембран являются соединениями гидрофильными Остатки жирных кислот фосфолипидов биологических мембран являются соединениями Гидрофобными Осмотический гемолиз может происходить при помещении эритроцитов в … раствор NaCl Гипотонический Коэффициентом распределения вещества называют равновесное соотношение концентраций исследуемого вещества в мембране и окружающей водной среде Коэффициент проницаемости Р вещества через мембрану имеет размерность: м/с Уравнение Нернста-Планка позволяет рассчитать величину плотности потока вещества через мембраны Активный транспорт ионов через биомембраны осуществляется за счёт энергии гидролиза макроэргических связей АТФ оэффициент проницаемости мембран определяется выражением P=Dk/l, где k: коэффициент распределения, характеризующий соотношение равновесных концентраций диффундирующего вещества в мембране и в окружающем растворе Коэффициент проницаемости мембран определяется выражением P=Dk/l, где l: толщина мембраны, D – коэффициент диффузии рассматриваемых частиц в веществе самой мембраны, К – коэффициент распределения, характеризующий соотношение равновесных концентраций диффундирующего вещества в мембране и в окружающем растворе Укажите, при каких условиях пассивный перенос катионов через мембрану может происходить из раствора, где его концентрация ниже, в более концентрированный раствор: под действием соответствующего электрического поля Пассивный перенос ионов описывается уравнением Нернста-Планка. Как модифицируется это уравнение, если ион превратится в незаряженную частицу? Уравнение Нернста-Планка превратится в уравнение Фика При условии, что мембрана проницаема только для ионов калия, уравнения Гольдмана-Ходжкина-Катца трансформируется в уравнение Нернста для ионов калия Укажите, при каких условиях при решении дифференциального уравнения Нернста-Планка получается уравнение Нернста? Если мембрана проницаема только для одного вида ионов и для этих ионов J=0 Структурной основой биологической мембраны являются белки Обязательным структурным компонентом биологических мембран являются соединения, состоящие из полярной «головки» и неполярного «хвоста», например, фосфолипиды Латеральная диффузия липидов и белков в биомембранах осуществляется значительнобыстрее, чем диффузия поперёк мембраны – из слоя в слой. Латеральная диффузия липидов и белков в биомембранах осуществляется значительно медленнее, чем диффузия поперек мембраны – из слоя в слой 10. 1) Вязкость липидного бислоя биомембран близка к вязкости воды.
Вязкость липидного бислоя биомембран значительно выше вязкости воды и близка к вязкости растительного масла.
Вещество диффундирует через мембрану тем легче, чем выше его коэффициент распределения.
5. 1) Вещество диффундирует через мембрану тем легче, чем меньше его коэффициент распределения. 2) Облегчѐнная диффузия – это перенос ионов специальными молекулами – переносчиками.
3) Облегчѐнной называют диффузию веществ, имеющих высокие значения коэффициента распределения.
6. 1) Диффузия заряженных частиц через мембраны подчиняется уравнению Фика для мембраны 2) Диффузия заряженных частиц в растворах подчиняется уравнению Нернста-Планка. 3) Диффузия незаряженных частиц через мембраны подчиняется уравнению Нернста-Планка. 4) Диффузия незаряженных частиц через мембраны подчиняется уравнению Фика для мембраны
7. 1) Коэффициент проницаемости мембраны для ионов калия выше, чем для ионов натрия или хлора, когда на мембране клетки генерируется потенциал покоя. 2) При возникновении потенциала действия коэффициент проницаемости мембраны для ионов натрия имеет самое высокое значение.
3) При возникновении потенциала действия коэффициент проницаемости мембраны для ионов хлора имеет самое высокое значение.
8. 1) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение только потенциала покоя, но не потенциала действия. 2) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение только потенциала действия, но не потенциала покоя.
3) Уравнение Гольдмана-Ходжкина-Каца описывает возникновение трансмембранной разности потенциалов на мембранах как в случае генерации потенциалов покоя, так и потенциалов действия. Диффузия незаряженных частиц через мембрану происходит под действием градиента потенциала электрического поля Диффузия незаряженных частиц через мембрану происходит под действием градиента концентрации ПРАВИЛЬНЫЕ Латеральная диффузия белков и липидов это перемещение их вдоль мембраны Сколько монослоев липидов в цитоплазматической мембране? Два Коэффициент проницаемости мембраны для ионов меньше, чем для воды (для ионов 10-10, для воды 10-2 Осмотический гемолиз может происходить при помещении эритроцитов в гипотонический раствор
Латеральная диффузия липидов и белков в биомембранах осуществляется значительно быстрее, чем диффузия поперёк мембраны – из слоя в слой??? Обязательным структурным компонентом биологических мембран являются соединения, состоящие из полярной «головки» и неполярного «хвоста», например, фосфолипиды Диффузия незаряженных частиц через мембраны подчиняется уравнению Фика для мембраны Диффузия заряженных частиц в растворах подчиняется уравнению Нернста-Планка Активный транспорт ионов через мембрану происходит в направлении градиентов концентрации и потенциала электрического поля Пассивный транспорт ионов через мембрану направлен в сторону, противоположную градиентам концентрации и потенциала электрического поля Активный транспорт ионов через мембрану происходит в направлении градиента концентрации и потенциала электрического поля Вещество диффундирует в данном растворителе тем легче, чем выше его коэффициент диффузии Вязкость липидного бислоя биомембран значительно выше вязкости воды и близка к вязкости растительного масла Диффузия ионов через мембрану происходит под действием градиентов концентрации и потенциала электрического поля Диффузия незаряженных частиц через мембрану происходит под действием градиента концентрации НЕПРАВИЛЬНЫЕ Коэффициент проницаемости мембраны для ионов больше, чем для воды Пассивный транспорт ионов через мембрану происходит в направлении градиентв концентрации и потенциала электрического поля Латеральная диффузия липидов и белков в биомембранах осуществляется значительно медленнее, чем диффузия поперёк мембраны – из слоя в слой??? Структурной основой биологической мембраны являются белки Диффузия незаряженных частиц через мембраны подчиняется уравнению Нернста-Планка Диффузия заряженных частиц через мембраны подчиняется уравнению Фика для мембраны Активный транспорт ионов через мембрану направлен в сторону, противоположную градиентам концентрации и потенциала электрического поля Вещество диффундирует через мембрану тем легче, чем ниже его коэффициент распределения Вязкость липидного бислоя биомембран близка к вязкости воды Диффузия ионов через мембрану происходит только под действием градиента потенциала электрического поля Диффузия незаряженных частиц через мембрану происходит под действием градиента потенциала электрического поля
Теги: Диффузия ионов в растворах подчиняется, диффузия незаряженных частиц в растворах подчиняется, уравнению Нернста-Планка, уравнению Фика
Теги: Плотность потока вещества, Градиент концентрации, Коэффициент проницаемости
Плотность потока вещества: моль/(м2*с) Коэффициент диффузии м2/с Коэффициент проницаемости м/с Коэффициент распределения: безразмерная величина Градиент потенциала: В/м Плотность потока вещества: моль/(м2/с)
Теги: при участии ионофоров – облегченная диффузия веществ происходит, без затраты энергии – пассивный транспорт происходит, при участии ферментов АТФаз – активный транспорт происходит Соотношение между напряженностью поля и градиентом потенциала определяется по формуле E=-dφ/dx Соотношение между потоком и плотностью потока вещества определяется по формуле Ф=JS Соотношение между плотностью потока и градиентом концентрации определяется по формуле J=-Ddc/dx Простая диффузия происходит через липидный слой Облегченная диффузия происходит в комплексе с переносчиком Диффузия через канал происходит при участии интегральных белков Пассивный транспорт происходит без затраты энергии Активный транспорт происходит при участии калий-натриевого насоса Облегченная диффузия ионов происходит при участии ионоформв Величина потенциала покоя подчиняется уравнению Гольдмана-Ходжкина-Катца Диффузия ионов подчиняется уравнению Нернста-Планка Диффузия незаряженных частиц подчиняется уравнению Фика Диффузия вещества через мембрану осуществляется тем легче, чем больше значение коэффициента проницаемости и тем труднее, чем меньше значение коэффициента ркаспределения. Пассивный транспорт вещества через мембрану осуществляется без затраты энергии. При возникновении стационарного трансмембранного потенциала суммарная плотность потока ионов равна нулю, но плотности потоков отдельных ионов не равны нулю. Возникновение потенциала покоя обусловлено, главным образом, высокой избирательной проницаемостью мембран для ионов калия. Возникновение потенциала действия обусловлено, главным образом, высокой избирательной проницаемостью для ионов натрия. Если мембрана обладает избирательной проницаемостью для одного вида ионов и их концентрация по обе стороны мембраны разная, то на мембране возникнет разность электрических потенциалов. Пассивный транспорт ионов через мембраны осуществляется за счет градиента их концентрации и градиента потенциала электрического поля. Такие процессы описываются уравнением J=-D(dc/dx+ZFc/RT…) Трансмембранная разность электрических потенциалов описываемая уравнением гольдмана-Ходжкина-Катца возникает в результате активного переноса ионов. Для ее возникновения необходимо, чтобы мембрана обладала неодинаковой проницаемостью для разных ионов и чтобы концентрации ионов различались по разные стороны мембраны. В каком физическом состоянии находится липидная часть биологической мембраны: жидкокристаллическом Величина, численно равная количеству вещества, перенесенного за единицу времени через единицу площади поверхности, перпендикулярной направлению переноса – это плотность потока Простая диффузия происходит путем диффузии вещества через липидные поры или каналы проницаемости Функцию биологической мембраны, которая обеспечивает селективный транспорт и распределение ионов между клеткой и средой называют барьерной В уравнении Фика для мембран J=P(C1-C2) C1 и C2 – это концентрации двух разных диффундирующих веществ в омывающих мембрану водных растворах В уравнении Фика для мембран P – это коэффициент проницаемости В уравнении Фика для однородных сред dc/dx – это градиент концентрации При фазовом переходе в гель-состояние толщина мембраны увеличивается Укажите уравнение Фика для мембран: J=P(C1-C2) Диффузия незаряженных частиц в растворах подчиняется уравнению Фика Диффузия незаряженных частиц через мембраны подчиняется уравнению Фика для мембран Диффузия ионов в растворах подчиняется уравнению Нернста-Планка Какова размерность коэффициента распределения вещества? безразмерная величина Лизосомы (липидные везикулы) представляют собой бислойные концентрические структуры Ионные каналы проницаемости в мембранах образуются интегральными белками Все мембранные липиды относятся к числу амфифильных соединений Коэффициент распределения вещества характеризует способность исследуемого вещества растворяться в биологических мембранах Основу структуры биологических мембран составляет двойной слой фосфолипидов Коэффициент проницаемости мембран определяется выражением P=Dk/l, где D – коэффициент диффузия рассматриваемых частиц в веществе самой мембраны Величина, численно равная количеству вещества, перенесенного за единицу времени через единицу площади поверхности, перпендикулярной направлению переноса – это плотность потока Как повлияет увеличение толщины мембраны на ее проницаемость при прочих неизменных условиях транспорта веществ? проницаемость уменьшится Что характеризует коэффициент распределения вещества k? вероятность возникновения каналов проницаемости для ионов в мембране Толщина биологической мембраны составляет: 10 нм Белки биологических мембран, пронизывающие бислой липидов насквозь, называются интегральными белками Матричная функция мембран состоит в том, что мембрана является основой для удержания белков Матричная функция биологической мембраны обеспечивает определенное взаимное расположение и ориентацию мембранных белков Отличие облегченной диффузии от простой заключается в том, что она осуществляется при участии молекул-переносчиков Диффузия через канал происходит при участии интегральных белков, простая диффузия происходит через липидный слой, облегченная диффузия происходит в комплексе с переносчиком Какова размерность коэффициента проницаемости P вещества через мембрану? м/с Являются ли биологические мембраны жидкими кристаллами? Да Какова размерность плотности потока вещества J? моль/(м2/с) При обработке ультразвуком или интенсивном встряхивании в смеси вода-гипид образуются сферические структуры называемые липосомы Укажите уравнение Нернста-Планка, описывающее диффузию заряженных частиц в растворах: (самое большая формула)
МЕХАНИЧЕСКИЕ СВОЙСТВА БИОЛОГИЧСКИХ ТКАНЕЙ. ФИЗИЧЕСКИЕ ВОПРОСЫ ГЕМОДИНАМИКИ Выберите правильный ответ: 1. Деформацией называется изменение взаимного расположения точек тела, которое приводит к изменению его формы и размеров, под действием внешних факторов; 2. При деформации растяжения внешняя сила направлена а) вдоль оси деформируемого тела; . 3. При деформации сдвига внешняя сила направлена б) по касательной к поверхности тела; . 4. Мерой деформации растяжения является... а) относительное удлинение;
5. Мерой деформации сдвига является б) относительный сдвиг;
6. Упругой называется деформация, которая г) полностью исчезает после прекращения действия силы.
Укажите формулу закона Гука: сигма=Е*эпсилон
Укажите единицу модуля упругости: Па
Уравнение Ламе позволяет определить связь между г) механическим напряжением в стенке сосуда и давлением внутри него. Уравнение Ламе имеет вид: сигма=p*r/H
Модель Франка позволяет установить связь между. в) ударным объемом крови, гидравлическим сопротивлением периферической части системы кровообращения и изменением давления в артериях;
Скорость пульсовой волны в крупных сосудах определяют выражением: v=
1) При длительном действии постоянной нагрузки во всех материалах проявляется вязкоупругая деформация. ДА 2) При больших внешних нагрузках ползучесть костной ткани моделируется системой, состоящей из "поршня" и "пружины", соединенных параллельно. НЕТ 3)Ползучесть изучается при действии постоянной силы на механическую систему. ДА 4) Релаксация напряжения зависит только от упругих свойств материала. НЕТ 5) Гладкие мышцы могут значительно растягиваться без особого напряжения, что способствует увеличению объема полых органов. ДА
В модели Франка артериальная часть системы кровообращения… ДА Скорость распространения пульсовой волны значительно больше скорости крови ДА Пульсовая волна распространяется со скоростью 5-10 м/с, следовательно, за время систолы она должна распространяться на расстояние 1,5-3 м ДА Модель Франка точно отражает весь процесс движения крови по артериальному руслу… НЕТ
Упруговязкие свойства биологических тканей моделируются системой, состоящей из комбинации двух моделей: «поршень» и «пружина» ДА Деформация называется пластической, если после прекращения действия внешней силы, тело не возвращается в исходное состояние Да Предел текучести – напряжение, начиная с которого деформация возрастает без увеличения напряжения ДА Механизм упругости полимеров и кристаллических мономеров одинаков, поэтому они обладают сходными механическими свойствами НЕТ В модели, состоящей из параллельно соединенных упругого и вязкого элементов, реализуется вязкоупругая необратимая деформация НЕТ
Уравнение Ламе определяет напряжение в крупном сосуде, которое прямо пропорционально давлению крови и радиусу стенки сосуда и обратно пропорционально ее толщине ДА Модель Франка позволяет определить скорость пульсовой волны НЕТ Давление в артериях после систолы экспоненциально убывает со временем ДА Механические свойства сосудов определяются, главным образом, свойствами коллагена, эластина и гладких мышечных волокон ДА Кровь движется по сосудам с разной скоростью, так как пульсовая волна убывает НЕТ Пределом упругости называют величину, равную наибольшему напряжению, при котором деформация сохраняет обратимый упругий характер Пределом прочности называют величину, равную наибольшему напряжению которое способен выдержать образец без разрушения По диаграмме растяжения определяют, в частности, значение предела упругости Диаграммой растяжения называют зависимость механического напряжения от относительной деформации твердых тел при растяжении Упругой называется деформация, которая после прекращения действия силы полностью исчезает Пластической называется деформация, которая не исчезает после снятия нагрузки, она необратимо изменяет начальные размеры образца При деформации сдвига внешняя сила направлена по касательной к поверхности тела При деформации растяжения внешняя сила направлена вдоль оси деформируемого тела Укажите единицу СИ модуля упругости Па или Н/м2 Закон Гука выполняется при любых способах деформирования тел, но только при малых деформациях и небольших значениях напряжения Относительной деформацией при растяжении называется величина, равная отношению абсолютного удлинения к первоначальной длине образца При упругой деформации происходит обратимое изменение формы образца При упругой деформации между механическим напряжением и относительной деформацией существует зависимость прямо пропорциональная Укажите единицу СИ абсолютной деформации при растяжении: м Механическим напряжением называется величина, равная отношению силы, приложенной к сечению, к площади сечения Деформацией называется изменение взаимного расположения точек тела, которое приводит к изменению его формы и размеров, под действием внешних факторов При определении механического напряжения при деформации растяжения и сжатия учитывается, в частности, площадь сечения образца, на которое действует деформирующая сила При действии деформирующей силы в образце возникают внутренние силы, мерой которых является механическое напряжение При упругой деформации растяжения происходит удлинение образца Деформацией, которая после прекращения действия силы полностью исчезает, называют деформацией упругой При деформации изгиба материал, находящийся в нейтральном слое не испытывает деформации растяжения или сжатия Укажите формулу для определения относительной деформации при одноосном растяжении:
Изгиб - это вид деформации, который характеризуется... срединного (нейтрального) слоя деформируемого объекта (балки, стержня) под действием внешних сил искривлением Модуль упругости численно равен: напряжению, при котором длина образца увеличивается вдвое ПРАВИЛЬНЫЕ УТВЕРЖДЕНИЯ Пластичность - свойство материала деформироваться без разрушения под действием внешних сил и сохранять новую форму после прекращения их действия Единицы СИ модуля упругости и механического напряжения одинаковы (измеряются в Паскалях) Предел прочности – величина, равная наибольшему напряжению которое образец способен выдержать без разрушения Единицей СИ предела прочности является МН/м2 или МПа. Предел упругости - напряжение, ниже которого деформация сохраняет упругий обратимый характер Сдвиг - вид деформации, возникающей в случае, когда на тело действует касательная сила, приложенная параллельно закрепленному основанию Закон Гука выполняется только при малых деформациях и небольших значениях напряжения Относительная деформация при растяжении (сжатии) - величина, равная отношению абсолютного удлинения к первоначальной длине образца При упругой деформации (сжатия) происходит обратимое изменение формы образца Относительная деформация - безразмерная величина Пластическая деформация - это деформация, которая не исчезает после снятия нагрузки, она необратимо изменяет начальные размеры образца Модуль Юнга численно равен механическому напряжению, при котором длина образца увеличивается вдвое Деформация при изгибе характеризуется стрелой прогиба Относительная деформация - безразмерная величина При упругой деформации растяжения происходит обратимое изменение формы образца
НЕПРАВИЛЬНЫЕ УТВЕРЖДЕНИЯ Упругая деформация проявляется в любых материалах при длительном действии постоянной нагрузки При деформации изгиба материал, находящийся в нейтральном слое подвергается деформации растяжения или сжатия Предел прочности - деформация, начиная с которой в образце развивается текучесть Растяжение (сжатие) - вид деформации, возникающей в случае, когда к стержню (бруску) с закрепленным основанием прикладывается сила F, направленная поперек его оси Относительная деформация при растяжении (сжатии) - величина, равная отношению конечной длины образца к его абсолютному удлинению
Закон Гука выполняется при любых деформациях и любых значениях напряжения Единицей СИ относительной деформации является м Модуль упругости при растяжении - напряжение, при котором длина образца уменьшается вдвое При длительном действии постоянной нагрузки во всех материалах проявляется вязкоупругая деформация Пластическая деформация - это деформация, которая частично исчезает после снятия напряжения Модуль Юнга численно равен механическому напряжению, при котором длина образца увеличивается на 50% Модуль упругости при растяжении - напряжение, при котором длина образца уменьшается вдвое Предел текучести - это относительная деформации, начиная с которой деформация становится текучей Относительная деформация измеряется в единицах длины Абсолютная деформация – безразмерная величина Растяжение (сжатие) – способ деформации, возникающей тогда, когда к стержню (бруску) с закрепленным основанием прикладывается сила, направленная поперек его оси Изгиб – способ деформации, характеризующийся деформацией срединной поверхности деформируемого объекта (балка, стержень) под действием внешних сил Абсолютная деформация при кручении характеризуется углом сдвига центральных точек одного основания относительно другого Относительная деформация сдвига – котангенс угла сдвига При действии деформирующей силы в образце возникает относительная деформация, которая зависит от размеров образца При действии деформирующей силы в образце возникают абсолютная деформация, которая не зависит от размеров образца Установите соответствия видов деформации и их характеристик угол сдвига – сдвиг, стрела прогиба – изгиб, относительное удлинение – растяжение/сжатие Абсолютное удлинение – м, относительное удлинение – безразмерная величина, механическое напряжение – Н/м2/Па, действующая сила – Н, относительный сдвиг – радиан/безразмерная величина, сила упругости – Н, модуль упругости - Па На приведенной ниже типичной диаграмме растяжения укажите участок кривой, соответствующий текучести материала – CD На приведенной ниже типичной диаграмме растяжения укажите участок кривой, соответствующий упругой деформации – 0B В приведенной формуле закона Гука Модуль упругости E, механическое наприжение – сигма, относительное удлинение - эпсилон Пределом прочности биологических тканей называют Механическое напряжение, при котором происходит разрушение; По какой формуле можно найти относительную деформацию? ε = D / l0; Деформация, которая возрастает без увеличения напряжения называется деформацией текучести Предел упругости – максимальное напряжение, при котором еще проявляется упругая деформация Предел прочности – напряжение, соответствующее наибольшей нагрузке, выдерживаемой перед разрушением Предел текучести – напряжение, начиная с которого деформация возрастает без увеличения напряжения Исследование механических свойств материалов проводят в двух режимах: изотоническом – ступенчато изменяют длину объекта и измеряют в новом состоянии изменение напряжения во времени, при этом получают кривые релаксации напряжения. Изометрическом - прикладывают определенную растягивающую силу и измеряют во времени длину системы, при этом получают кривые ползучести. При упругой деформации растяжения происходит... 1) удлинение образца; Мерой такой деформации является: 1) относительное удлинение; При действии деформирующей внешней силы в теле возникают внутренние силы, мерой этих сил является механическое напряжение. Для упругой деформации растяжения закон Гука записывается в виде: сигма=Е*эпсилон
Практически все материалы обладают 1) ползучестью; Это выражается в
|
|||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.37.200 (0.015 с.) |



 Теги: вдоль плоскости мембран – латеральная диффузия, в сторону противоположную направлению градиентов концентрации и потенциалов – активный транспорт, в направлении градиентов концентрации и потенциала – пассивный транспорт
Теги: вдоль плоскости мембран – латеральная диффузия, в сторону противоположную направлению градиентов концентрации и потенциалов – активный транспорт, в направлении градиентов концентрации и потенциала – пассивный транспорт Теги: в комплексе с переносчиком – облегченная диффузия происходит, через липидный слой – простая диффузия происходит, при участии интегральных белков – диффузия через канал происходит
Теги: в комплексе с переносчиком – облегченная диффузия происходит, через липидный слой – простая диффузия происходит, при участии интегральных белков – диффузия через канал происходит