
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Определение частоты звуковой волны методом резонансаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Приборы и принадлежности: сообщающиеся сосуды, заполненные частично водой, звуковой генератор, прибор ФП – 42 А, осциллограф.
Краткая теория
Периодическое отклонение тела от положения равновесия называется колебанием. Колебания, лежащие в интервале от 20 до 20000 Гц, обладают свойством вызывать ощущения звука и могут быть выделены по этому признаку в особую группу – группу звуковых колебаний (акустических колебаний), называемых звуком. С физической точки зрения колебания названных частот ничем не отличаются от механических колебаний других частот. Рассмотрим механизм образования волн. Колеблющееся тело, находящееся в упругой среде, приводит в колебательное движение соприкасающиеся с ним частицы среды, вследствие чего в прилегающих к этому телу элементах среды возникают периодические деформации. Деформации (например, сжатия или растяжения) ведут к возникновению упругих сил, которые стремятся элементы среды вернуть в первоначальное состояние равновесия, т.е. возникают упругие колебания среды, т.к. соседние элементы среды взаимодействуют друг с другом, то эти упругие деформации будут передаваться от одних участков среды к другим. Процесс распространения колебательного движения в среде называется волной или волновым процессом. Волны являются продольными, если частицы среды колеблются вдоль линий распространения колебаний, и поперечными, если частицы среды колеблются перпендикулярно направлению распространения волн. При возникновении продольных волн играет роль деформация попеременного растяжения и сжатия. В возникновении поперечных волн в среде играет роль периодически колеблющаяся деформация сдвига. В твёрдых телах возникают упругие деформации растяжения, сжатия и сдвига, поэтому в твёрдых телах могут распространяться продольные и поперечные волны. В жидкостях и газах возникают только продольные волны, распространяющиеся в виде чередующихся сжатий и разрежений (исключение составляет поверхность жидкости). Так как в жидкости и газе деформации сдвига неупругие, то поперечные волны возникнуть в них не могут. Если сдвинуть один слой относительно другого, то в противоположность твёрдым телам, сдвинутые слои не стремятся вернуться в исходное положение. Волна, проходящая через данную точку среды, характеризуется определённым направлением распространения. Область пространства, внутри которой колеблются все частицы среды, называется волновым полем. Граница, отделяющая колеблющиеся частицы от частиц ещё не начавших колебаться, носит название фронта волны. Фронтом волны называется геометрическое место точек, до которых дошли колебания в данный момент времени. Понятие фронта волны не следует смешивать с понятием волновой поверхности. Геометрическое место точек, колеблющихся в одинаковой фазе, называется волновой поверхностью. Волновую поверхность можно провести через любую точку пространства, охваченную волновым процессом. Следовательно, волновых поверхностей существует бесконечное множество, в то время как волновой фронт в каждый момент времени только один. Волновые поверхности могут быть любой формы. В простейших случаях они имеют форму плоскости или сферы. Соответственно в этих случаях волна называется плоской или сферической. В плоской волне волновые поверхности представляют собой систему параллельных друг другу плоскостей, в сферической – систему концентрических сфер. Всё время пока существует волна, частицы совершают колебания около своих положений равновесия, причём различные частицы колеблются со сдвигом по фазе. Расстояние между ближайшими частицами, колеблющимися одинаково (в одинаковой фазе) называется длиной волны λ. Длина волны равна тому расстоянию, на которое распространяется волна за период
где υ – скорость распространения волны, T – период Любую волну характеризуют три основные величины: длина волны λ, скорость υ и частота ν.
Уравнение волны Пусть некоторая точка O участвует в гармоническом колебательном движении с амплитудой
Колебания, распространяясь в среде, дойдут до точки A, рис. 2 лежащей на расстоянии r от точки O, через время
Скорость υ имеет положительный знак, если направление скорости совпадает с направлением оси r и – отрицательной, если скорость направлена против оси. Если волна идёт не затухая от точки O в сторону точки A, отстоящей от O на расстояние r, то смещение точки A определяется по формуле (1), но в новый более поздний момент времени
учитывая (2), получим:
Выражение (3) представляет собой уравнение плоской волны, распространяющейся вдоль прямой OA, которое ещё иначе называется уравнением плоской бегущей волны. Оно определяет для любого момента времени t отклонение от положения равновесия колеблющихся частиц Учтём известные соотношения
где ν – частота, И тогда можно записать:
Выражение (3) можно преобразовать к виду:
или
Звуковые волны могут интерферировать. Рассмотрим случай интерференции двух волн одинаковой частоты, длины и амплитуды, распространяющихся в противоположных направлениях. На опыте это можно осуществить, если на пути бегущей волны перпендикулярно к направлению распространения поставить хорошо отражающую преграду. В результате интерференции волны падающей и волны отражённой возникает так называемая стоячая волна. Выведем уравнение стоячей волны. Падающая (бегущая) волна, распространяющаяся по направлению оси r, описывается уравнением:
а отражённая
В скобке (–) поменялся на (+) за счет того, что у скорости отражённой волны поменялось направление на противоположное (отражённая волна движется против оси r). Уравнение стоячей волны получится при сложении уравнений бегущеё и отражённой волн:
Вынося общий множитель а и используя формулу суммы двух косинусов, находим:
то
Уравнение стоячей волны запишется:
В этом уравнении множитель
не зависящий от времени, выражает результирующую амплитуду A
Так как функция
будут иметь наибольшую амплитуду:
откуда
где
Точки, для которых
Из отношений (7) и (8) следует, что расстояние между соседними узлами (или соседними пучностями) в стоячей волне равно В уравнении стоячей волны множитель На рис. 4 дан ряд моментальных фотографий отклонений точек от положения равновесия. Первая соответствует моменту, когда отклонения достигают наибольшего абсолютного значения. Последующие рисунки сделаны с интервалами в четверть периода.
Рассмотрим несколько примеров колебаний сплошных систем. В закреплённой с обоих концов натянутой струне при возбуждении поперечных колебаний устанавливаются стоячие волны, причём в местах закрепления струны должны располагаться узлы. Поэтому в струне возбуждаются только такие колебания, половина длины волны которых укладывается на длине струны целое число раз. Отсюда вытекает условие
где
Подобным образом можно рассматривать собственные колебания столба воздуха, заключённого в трубе с открытыми концами. В этом случае на концах образуется пучности стоячей волны, т.к. отражаясь от менее плотной среды волна не меняет фазы в месте отражения. Как и в предыдущем случае на всей длине столба воздуха уложится целое число
В системе с неодинаковыми условиями отражения волн на концах, например, в воздушном слое трубы, закрытой только у одного конца, также можно возбудить собственные колебания. Стоячие волны в этом случае имеют на открытом конце пучность, а на закрытом – узел стоячей волны. На всей длине столба воздуха
Случай возникновения стоячей волны в столбе воздуха используют для нахождения частоты этих колебаний.
Источником звука в данной работе служит звуковой генератор. Для определения длины волны издаваемого генератором звука, пользуются стоячими волнами, образующимися в стеклянной трубке, которая закрыта с одного конца подвижной преградой. Если у открытого конца трубы поместить телефон, соединённый с генератором звука, то колебания его мембраны передаются воздушному столбу в трубке. Воздушный столб будет резонировать только в том случае, если период его собственных колебаний совпадает с периодом колебаний звука, издаваемого генератором (явление резонанса). Звуковая волна от телефона, размещённого у открытого конца трубки, распространяясь по воздуху, дойдёт до преграды, находящейся на втором конце трубки, поменяет фазу на противофазу и пойдёт навстречу бегущей волне. Бегущая и отражённая волны создадут стоячую волну. У поверхности преграды всегда образуется узел, у открытого конца трубки – пучность. В зависимости от высоты воздушного столба, а также от частоты колебаний мембраны в трубке расположится то или иное число узлов и пучностей стоячей волны. Звук мембраны усиливается, когда она оказывается в пучностях стоячей волны. Длина самого короткого воздушного столба, которая резонирует мембране телефона, имеет узел у преграды и пучность у открытого конца трубки; следовательно, длина его равна четверти длины звуковой волны в воздухе. Если трубка достаточно длинная, то резонанс в трубке может повториться, когда высота столба воздуха будет равна трём, пяти или другому нечётному числу четвертей длины звуковой волны в воздухе. Необходимо заметить, что у открытого конца трубки всегда имеется некоторое смещение пучностей. Чтобы учесть его, при измерении вводят так называемую поправку на открытый конец, которая не зависит от длины волны и равна приблизительно 0,6R, где R – радиус трубки. Если
Отсюда
где
где Подставив это в рабочую
1 вариант работы Описание прибора
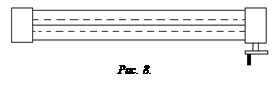
Прибор для определения длины звуковой волны изображён на рис. 7. Это сообщающиеся сосуды, состоящие из стеклянных трубок A и B, соединённых резиновой трубкой. Трубки A и B крепятся на вертикальном штативе с сантиметровым шаблоном, причём сосуд B может легко перемещаться и крепиться в любом месте штатива. В сообщающиеся сосуды налита вода. Уровень воды в трубке A служит подвижной преградой. Над открытым концом этой трубки закреплена мембрана телефона, которая колеблется с такой же частотой, как и частота звука, издаваемого генератором.
Выполнение работы
Включить звуковой генератор, настроив его на определённую частоту. Поднять сосуд B настолько, чтобы уровень воды в трубке A подошёл к верхнему её краю.
Определить температуру
2 вариант работы Описание прибора ФП – 42 А Прибор представляет собой горизонтальную трубу на подставках, внутри которой перемещается капсюль ДЭМШ – 1 А. Перед открытым концом трубы располагается заглушка с другим капсюлем МД – 201. Заглушка может закрывать отверстие трубы. К одному из капсюлей (телефону) подаётся напряжение звуковой частоты от звукового генератора ЗГ-1. Звуковые колебания, преобразованные другим капсюлем (микрофоном) в электрический сигнал, подаются на вертикальный выход электронного осциллографа типа ЭОТ. Вращая рукоятку, расположенную справа, перемещают капсюль т трубе и находят такие его положения, при которых амплитуда сигнала на экране осциллографа максимальна. Это положение соответствует расстоянию между капсюлями (если труба закрыта) или между капсюлем и краем трубы (если труба открыта), кратному числу полуволн. Длина звуковой воны определяется как удвоенная разность отсчётов по шкале между двумя последовательными максимумами.
Выполнение работы
Включить звуковой генератор, настроив его на определённую частоту. Вращая рукоятку, перемещают капсюль в трубе и находят положение максимумов, по максимальной амплитуде сигнала на экране осциллографа, замеряют длину резонирующего столба воздуха и по формуле (2) определяют частоту колебаний. Результаты измерений занести в таблицу.
Задачи 1. Частота колебаний камертона 440 Гц. Какова длина звуковой волны, распространяющейся от камертона в воздухе. Скорость звука в воздухе 332 м/с. Ответы: 1) 0,44 м; 2) 2,35 м; 3) 0,8 м; 4) 1,32 м; 5) 0,75 м.
2. Определите длину волны λ, если расстояние ∆ℓ между первым и четвертым узлами стоячей волны равно 30 см. Ответы: 1) 23,8 см; 2) 15,8 см; 3) 30 см; 4) 20 см; 5) 18 см.
3. Звуковые колебания распространяются в воде со скоростью 1480 м/с, а в воздухе со скоростью 340 м/с. Во сколько раз изменится длина звуковой волны при переходе звука из воздуха в воду. Ответы: 1) 7,32; 2) 4,35; 3) 9,3; 4) 2,78; 5) 5,26.
4. Найдите разность фаз между двумя точками звуковой волны, отстоящими друг от друга на расстоянии 25 см, если частота колебаний 680 Гц. Скорость звука в воздухе 340 м/с. Ответы: 1) π/2; 2)
5. Расстояние между второй и шестой пучностями стоячей волны 20 см. Определить длину стоячей волны. Ответы: 1) 0,22 м; 2) 0,1 м; 3) 0,33 м; 4) 0,42 м; 5) 0,11 м.
6. Скорость звука в воде 1450 м/с. На каком расстоянии друг от друга вдоль направления распространения волны находятся точки, совершающие колебания в противоположных фазах, если частота колебаний равна 731 Гц. Ответы: 1) 0,533 м; 2) 0,78 м; 3) 0,63 м; 4) 0,992 м; 5) 1,10 м. Контрольные вопросы 1. Что называется механическим колебанием? 2. Какие колебания называются звуковыми? 3. Что называется периодом, частотой, фазой, смещением, амплитудой колебательного движения? 4. Что называется длиной волны? Какие волны называются поперечными и продольными волнами. 5. В чём состоит явление интерференции? 6. Что представляет собой стоячая волна. Записать уравнение стоячей волны. 7. Что называется узлом, пучностью стоячей волны? 8. В чём состоит явление резонанса звука? 9. Написать формулу зависимости скорости звука от температуры. 10. Каково условие возникновения стоячей волны? 11. Как колеблются точки стоячей волны: 12. а) заключённые между двумя соседними узлами; 13. б) лежащие по разные стороны от узла? 14. Вывод рабочей формулы.
ЛИТЕРАТУРА
1. Савельев И. В. Курс общей физики, т. 2. М.: Наука, 1989. с.274–277, 289–291. 2. Зисман Г. А., Тодес О. М. Курс общей физики, т. 1, Наука, 1972. 3. Трофимовa Т. И. Курс физики. М.:, Высшая школа, 2002, с.284–291. Лабораторная работа 1.18
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 835; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.195.84 (0.009 с.) |


 ,
, и круговой (циклической) частотой ω. Тогда её смещение от положения равновесия
и круговой (циклической) частотой ω. Тогда её смещение от положения равновесия  можно описать уравнением:
можно описать уравнением: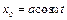 (1)
(1)
 . (2)
. (2)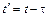 (новая точка придёт в колебание с некоторым запаздыванием на время
(новая точка придёт в колебание с некоторым запаздыванием на время 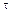 ), тогда
), тогда
 (3)
(3)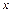 .
.
 – период колебания.
– период колебания.
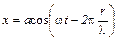
 .
.





 , т.к.
, т.к. 
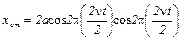 .
. (4)
(4) ,
,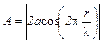 (5)
(5)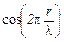 может принимать значения в пределах от нуля до единицы, то точки в стоячей волне, для которых
может принимать значения в пределах от нуля до единицы, то точки в стоячей волне, для которых (6)
(6)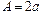 . Такие точки стоячей волны называются пучностями, их координаты определяются из равенства (6)
. Такие точки стоячей волны называются пучностями, их координаты определяются из равенства (6) ,
, , (7)
, (7)
 , имеют амплитуду, равную нулю и называются узлами стоячей волны. Их координаты находятся из условия
, имеют амплитуду, равную нулю и называются узлами стоячей волны. Их координаты находятся из условия , откуда
, откуда  (8)
(8) . Из (5) следует, что амплитуда стоячей волны зависит от координаты r колеблющейся точки, т.е. у разных точек среды разные амплитуды, чего в бегущей волне не наблюдается.
. Из (5) следует, что амплитуда стоячей волны зависит от координаты r колеблющейся точки, т.е. у разных точек среды разные амплитуды, чего в бегущей волне не наблюдается. при переходе через нулевое значение меняет знак, в соответствии с этим фаза колебаний по разные стороны от узла отличается на
при переходе через нулевое значение меняет знак, в соответствии с этим фаза колебаний по разные стороны от узла отличается на  , т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одной и той же фазе).
, т.е. точки, лежащие по разные стороны от узла, колеблются в противофазе, а все точки, заключенные между двумя соседними узлами, колеблются синфазно (т.е. в одной и той же фазе). Вторая соответствует одновременному прохождению частиц через положение равновесия. Третья фотография соответствует одновременному отклонению частиц, но в другую сторону (стрелками показаны скорости частиц).
Вторая соответствует одновременному прохождению частиц через положение равновесия. Третья фотография соответствует одновременному отклонению частиц, но в другую сторону (стрелками показаны скорости частиц).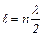 или
или 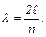 (9)
(9) – длина струны, а
– длина струны, а 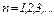


 где
где 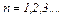
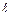 уложится или
уложится или 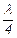 , или
, или 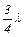 , или
, или 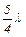 , и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию:
, и т.д., т.е. длины стоячих волн, устанавливающихся в воздушном столбе, открытом с одного конца, должны удовлетворять условию: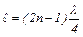 , где
, где 
 (11)
(11) – длина первого, самого короткого столба воздуха, дающего резонанс;
– длина первого, самого короткого столба воздуха, дающего резонанс;  – длина второго, то
– длина второго, то
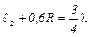

 . Подставив это выражение в (10), получим рабочую формулу:
. Подставив это выражение в (10), получим рабочую формулу: ,
,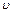 – скорость звука при данной температуре
– скорость звука при данной температуре 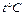 . Для определения скорости звука при данной температуре t пользуются формулой
. Для определения скорости звука при данной температуре t пользуются формулой

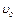 = 332
= 332  – скорость звука при
– скорость звука при 
 (12)
(12) Перемещением сосуда B найти такое положение уровня воды в трубке A, при котором столб воздуха в ней резонировал бы на данную частоту колебаний. Это будет соответствовать установившейся стоячей волне. В этом случае у открытого конца трубки образуется пучность, которая обнаруживается по усилению звука. Определить по масштабу с точностью до 0,5 см длину резонирующего воздушного столба. Пусть она будет
Перемещением сосуда B найти такое положение уровня воды в трубке A, при котором столб воздуха в ней резонировал бы на данную частоту колебаний. Это будет соответствовать установившейся стоячей волне. В этом случае у открытого конца трубки образуется пучность, которая обнаруживается по усилению звука. Определить по масштабу с точностью до 0,5 см длину резонирующего воздушного столба. Пусть она будет  , при которой осуществляется опыт. Результаты измерений занести в таблицу.
, при которой осуществляется опыт. Результаты измерений занести в таблицу.

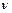

 π; 3) 2 π; 4) π; 5)
π; 3) 2 π; 4) π; 5)  π.
π.


