
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругие волны в сплошной средеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Механические возмущения, распространяющиеся в упругой среде с конечной скоростью, называются упругими или механическими волнами. Тела, которые, воздействуя на упругую среду, вызывают эти возмущения, называют источниками упругих волн. Упругая волна называется продольной, если частицы среды колеблются в направлении распространения волны. Упругая волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. В жидкостях и газах упругие волны всегда продольные. В твердых телах могут распространяться и продольные, и поперечные волны. Распространение в упругой среде механических возмущений, возбуждаемых источником волн, связано с переносом энергии. Поэтому такие волны называются бегущими волнами. Скорость распространения возмущений в среде v называется скоростью волны (фазовой скоростью). Скорость распространения упругих волн зависит от плотности и упругих свойств среды. Линия, касательная к которой в каждой ее точке совпадает с направлением распространения волны, называется лучом. Геометрическое место точек, в которых фаза колебаний частиц среды имеет одно и то же значение, называется волновой поверхностью. В однородной среде волновые поверхности перпендикулярны лучам. В зависимости от формы волновых поверхностей различают плоские, сферические, цилиндрические и другие волны (рисунок 1.7).
Уравнение плоской волны, распространяющейся вдоль оси Ox (в положительном направлении), имеет вид:
Если волна распространяется в отрицательном направлении оси Ox, то:
Если колебания частиц в волне гармонические, то волна называется гармонической или монохроматической. Уравнение плоской гармонической волны, бегущей вдоль оси Ox, может быть записано в виде:
Здесь A – амплитуда колебаний в волне, Расстояние, на которое распространяется волна за время, равное периоду колебаний, называется длиной волны λ (м):
С учетом этого волновое число можно представить в виде:
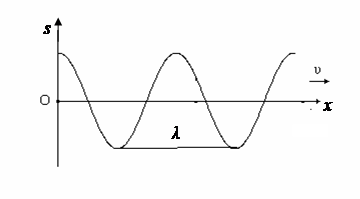
График зависимости s (x) в плоской гармонической волне для некоторого момента времени t представлен на рисунке 1.8.
В случае, когда плоская волна распространяется в произвольном направлении, ее уравнение имеет вид:
Здесь Экспоненциальная форма записи уравнения плоской волны:
Уравнение расходящейся сферической волны:
В случае монохроматической сферической волны:
Дифференциальное уравнение, описывающее распространение волн в однородной изотропной непоглощающей среде со скоростью v, называется волновым уравнением и имеет вид:
где Если волна гармоническая, то
Это уравнение называется уравнением Гельмгольца. Амплитуда, начальная фаза и частота волны определяются колебаниями в источнике волн. Фазовая скорость волны, как уже было сказано выше, зависит от физических свойств среды, в которой распространяется волна.
2 Звуковые волны в воздухе
2.1 Основные определения
Звуковыми волнами (звуком) называется процесс распространения упругих колебаний малой амплитуды в сплошной среде. Область среды, в которой распространяются звуковые волны, называется звуковым полем. При распространении звуковых волн в газах и жидкостях смещение частиц среды происходят в направлении распространения волн. Такие волны называются продольными. Теория звука в ее классической форме строится на основе законов движения жидкости и газа с учетом ряда особенностей колебательных движений с малой амплитудой. Движение жидкости и газа подчиняется законам гидро- и аэродинамики. Так как для жидкости и газа они записываются в одинаковой математической форме, то мы будем говорить об уравнениях гидродинамики, подразумевая под жидкостью также и газ. Уравнения гидродинамики в общей форме являются нелинейными и весьма трудно поддаются решению. Однако путем ряда предположений можно привести их к более простой форме. Перечислим основные упрощающие предположения, справедливые для звуковых волн в воздухе: а) пренебрегаем вязкостью и теплопроводностью воздуха; б) считаем воздух однородной, изотропной, линейной средой; в) предполагаем, что амплитуды колебаний давления, плотности и температуры звуковой волны малы; г) процессы сжатия и расширения в звуковой волне считаем адиабатическими. Введем ряд обозначений. Пусть ρ 0 и Р 0 – плотность и давление воздуха в состоянии равновесия. Тогда при распространении звука в среде общее давление в произвольной точке равно:
Величину δp, которая в звуковых процессах в газах обычно мала по сравнению с Р 0, будем обозначать далее через p = p (x, y, z, t) и называть звуковым давлением. Соответственно для плотности:
где
Величину Аналогично температуру среды можно представить в виде:
Т = Т 0 + δТ (x, y, z, t) где
|
||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1043; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.01 с.) |

 Рисунок 1.7 – Плоская и сферическая волны
Рисунок 1.7 – Плоская и сферическая волны

 .
. - циклическая частота волны,
- циклическая частота волны,  - волновое число,
- волновое число,  - фаза волны.
- фаза волны.

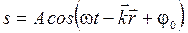
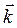 - волновой вектор. Его модуль равен волновому числу k, а направление совпадает с направлением распространения волны в точке с радус-вектором
- волновой вектор. Его модуль равен волновому числу k, а направление совпадает с направлением распространения волны в точке с радус-вектором  .
.



 - оператор Лапласа.
- оператор Лапласа. , и волновое уравнерие принимает вид:
, и волновое уравнерие принимает вид: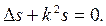

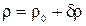 ,
, <<1.
<<1. называют относительным изменением плотности.
называют относительным изменением плотности. << 1 - относительная акустическая добавка к температуре.
<< 1 - относительная акустическая добавка к температуре.


