
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Упругие волны. Продольные и поперечные. Ур-я плоской волны. Фазовая ск-ть.Содержание книги
Поиск на нашем сайте
Упругие волны. Продольные и поперечные. Ур-я плоской волны. Фазовая ск-ть. Тело или среда наз упругой, если его деформации, вызываемые внешними возд-ями, полностью исчезают после прекращения этих возд-й. Если в каком-либо месте среду возбудить колеб-е частиц, то вследствие взаимод-я между частицами это колеб-е будет распростр-ся в среде, передаваться от частицы к частице с некотой скоростью. Пр-с распростр-я колеб-й в упругой среде наз упругой волной. Частицы среды, в котой распростр-ся волна, не переносятся волной, они лишь совершают колеб-я около своих положений =весия. Если частицы среды колеблются в направлении перпендикулярном распростр-ю волны, то такие волны наз поперечными. Если частицы среды колеблются вдоль направления распростр-я волны, то такая волна наз продольной.
Скорость распростр-я волны – скорость перемещения фазы, поэтому наз фазовая скорость. Волновое ур-е плоской волны, считая начальную фазу =й 0.
2 Ур-е сферич волны. Волновое ур-е. Волновая пов-ть. Волновой фронт.
Геометр-ое место точек, колеблющихся в одинаковой фазу, наз волновой пов-тью. Геометр-ое место точек, до котых, доходя колеб-я к моменту времени t, наз фронт волны. Волновые пов-ти неподвижны. А волновой фронт перемещается. Волновые пов-ти могут быть любой формы. Волна наз сфер-ой, если её волновая пов-ть имеет вид сферы. А несколько волновых пов-тей имеют вид концентрических сфер.: Из ур-й Максвелла в диф.форме можно получить диф-е ур-е 2ого порядка для векторов
Всякая ф-я, удовл-я таким ур-м опис-т волну. Решением 1ого ур-я явл-ся:
Упругие волны. Продольные и поперечные. Ур-я плоской волны. Фазовая ск-ть. Тело или среда наз упругой, если его деформации, вызываемые внешними возд-ями, полностью исчезают после прекращения этих возд-й. Если в каком-либо месте среду возбудить колеб-е частиц, то вследствие взаимод-я между частицами это колеб-е будет распростр-ся в среде, передаваться от частицы к частице с некотой скоростью. Пр-с распростр-я колеб-й в упругой среде наз упругой волной. Частицы среды, в котой распростр-ся волна, не переносятся волной, они лишь совершают колеб-я около своих положений =весия.
Если частицы среды колеблются в направлении перпендикулярном распростр-ю волны, то такие волны наз поперечными. Если частицы среды колеблются вдоль направления распростр-я волны, то такая волна наз продольной.
Скорость распростр-я волны – скорость перемещения фазы, поэтому наз фазовая скорость. Волновое ур-е плоской волны, считая начальную фазу =й 0.
2 Ур-е сферич волны. Волновое ур-е. Волновая пов-ть. Волновой фронт.
Геометр-ое место точек, колеблющихся в одинаковой фазу, наз волновой пов-тью. Геометр-ое место точек, до котых, доходя колеб-я к моменту времени t, наз фронт волны. Волновые пов-ти неподвижны. А волновой фронт перемещается. Волновые пов-ти могут быть любой формы. Волна наз сфер-ой, если её волновая пов-ть имеет вид сферы. А несколько волновых пов-тей имеют вид концентрических сфер.: Из ур-й Максвелла в диф.форме можно получить диф-е ур-е 2ого порядка для векторов
Всякая ф-я, удовл-я таким ур-м опис-т волну. Решением 1ого ур-я явл-ся:
|
|||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 186; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.214.16 (0.006 с.) |

 - ур-е плоской волны. А – амплитуда волны,
- ур-е плоской волны. А – амплитуда волны,  -фаза волны,
-фаза волны,  -начальная фаза.
-начальная фаза. .
. α=0. Найдем проводную по времени и координате:
α=0. Найдем проводную по времени и координате: ;
;  ;
; 
 - ур-е сфер-ой волны. А-амплитуда колеб-й на расст-и от источника = единице длины. Амплитуда сфер-ой волны убывает в зависимости от r (расст-я от источника).
- ур-е сфер-ой волны. А-амплитуда колеб-й на расст-и от источника = единице длины. Амплитуда сфер-ой волны убывает в зависимости от r (расст-я от источника). Эти диф.ур-я явл волновыми:
Эти диф.ур-я явл волновыми: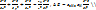
 ;
; А 2ого:
А 2ого:  где
где  – амплит-е зн-я вект-в. W-циклич.частота волны, k-волновой вект, x-коорд т., до которой дошла волна,
– амплит-е зн-я вект-в. W-циклич.частота волны, k-волновой вект, x-коорд т., до которой дошла волна, 


