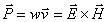Поперечные бегущие волны, распространяющейся вдоль струны»

Если при распространении волны частицы среды испытывают смещение в направлении, перпендикулярном направлению распространения, такая волна называется поперечной.

 

Примером волны такого рода могут служить волны, бегущие по натянутому резиновому жгуту или по струне. Как в поперечных, так и в продольных волнах не происходит переноса вещества в направлении распространения волны. В процессе распространения частицы среды лишь совершают колебания около положений равновесия. Однако волны переносят энергию колебаний от одной точки среды к другой.

- волна, у к-рой характеризующая её векторная величина лежит в плоскости, перпендикулярной направлению распространения волны. П. в. обладает поляризацией, т. е. вектор её амплитуды определ. образом ориентирован в поперечной плоскости. В частности, различают линейную, круговую и эллиптич. поляризации в зависимости от формы кривой, к-рую описывает конец вектора амплитуды.

 

Звуковые волны в газах»

 

Звуковыми волнами называются распространяющиеся в среде упругие волны, обладающие частотами в пределах 16—20000 Гц. Волны указанных частот, воздействуя на слуховой аппарат человека, вызывают ощущение звука. Звуковые волны в газах и могут быть только продольными, так как газы обладают упругостью лишь по отношению к деформациям сжатия (растяжения). Интенсивностью звука (или силой звука) называется величина, определяемая средней по времени энергией, переносимой звуковой волной в единицу времени сквозь единичную площадку, перпендикулярную направлению распространения волны:

Чувствительность человеческого уха различна для разных частот. Для того чтобы вызвать звуковое ощущение, волна должна обладать некоторой минимальной интенсив­ностью, но если эта интенсивность превышает определенный предел, то звук не слышен и вызывает только болевое ощущение. Таким образом, для каждой частоты колебаний существуют наименьшая (порог слышимости) и наибольшая (порог болевого ощущения) интенсивности звука, которые способны вызвать звуковое восприятие.

в среде распространяется волна с частотой колебаний, равной частоте ее источника, и с определенной скоростью, зависящей от плотности и упругих свойств среды. Скорость распространения звуковых волн в газах вычисляется по формуле

где R — молярная газовая постоянная, М — молярная масса, g=С_р/С_V — отношение молярных теплоемкостей газа при постоянных давлении и объеме, Т — термодинамическая температура. Скорость звука в газе не зависит от давления р газа, но возрастает с повышением температуры. Чем больше молярная масса газа, тем меньше в нем скорость звука.

3 Электромагнитные волны

3.1Вывод волнового уравнения для электромагнитного поля, фазовая скорость для электромагнитных волн

Для электромагнитной волны любой частоты фазовая скорость, измеренная в направлении волнового вектора, всегда равна одной и той же величине — скорости света в вакууме, универсальной константе.
В средах закон дисперсии электромагнитных волн достаточно сложен, и фазовая скорость может заметно меняться.
Фазовая скорость может превосходить скорость света в вакууме, и нередко ее превосходит.

Часто (а именно если выбрать достаточно большой угол с волновым вектором), фазовая скорость любой, даже сколь угодно медленной, волны может превышать скорость света, стремясь к бесконечности при стремлении угла к прямому.
В частности, фазовая скорость света (или вообще любой бегущей электромагнитной волны) в вакууме, измеренная по любому направлению, не совпадающему с ее волновым вектором, всегда больше скорости света.

3.2 Плоская бегущая электромагнитная волна в непроводящей среде. Вывод ее свойств: поперечность, отношение Е/Н, плотность энергии, фазовая скорость

 

Поток энергии электромагнитной волны, вектор Пойнтинга

 

Вектор плотности потока энергии электромагнитной волны называется вектором Умова-Пойнтинга, или чаще просто вектором

 

Пойнтинга Р: