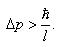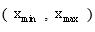Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частицы в бесконечной потенциальной яме. Квантовая энергия связанных частиц»Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Проведем качественный анализ решений уравнения Шредингера применительно к частице в одномерной прямоугольной «потенциальной яме» с бесконечно высокими «стенками». Такая «яма» описывается потенциальной энергией вида (для простоты принимаем, что частица движется вдоль оси х)
где l — ширина «ямы», а энергия отсчитывается от ее дна Уравнение Шредингера для стационарных состояний в случае одномерной задачи запишется в виде
По условию задачи (бесконечно высокие «стенки»), частица не проникает за пределы «ямы», поэтому вероятность ее обнаружения (а следовательно, и волновая функция) за пределами «ямы» равна нулю. На границах «ямы» (при х= 0 и х= 1) непрерывная волновая функция также должна обращаться в нуль. Следовательно, граничные условия в данном случае имеют вид
В пределах «ямы» (0 £ х £ l) уравнение Шредингера сведется к уравнению
Тогда
Условие y (l) =A sin kl = 0 выполняется только при kl = np, где n — целые числа, т. е. необходимо, чтобы
т. е. стационарное уравнение Шредингера, описывающее движение частицы в «потенциальной яме» с бесконечно высокими «стенками», удовлетворяется только при собственных значениях Еn, зависящих от целого числа п. Следовательно, энергия Еn частицы в «потенциальной яме» с бесконечно высокими «стенками» принимает лишь определенные дискретные значения, т.е. квантуется. Квантованные значения
энергии Еn называются уровнями энергии, а число п, определяющее энергетические уровни частицы, называется главным квантовым числом. Таким образом, микрочастица в «потенциальной яме» с бесконечно высокими «стенками» может находиться только на определенном энергетическом уровне Еn, или, как говорят, частица находится в квантовом состоянии n.
найдем собственные функции:
Постоянную интегрирования А найдем из условия нормировки, которое для данного случая запишется в виде
собственные функции будут иметь вид
энергетический интервал между двумя соседними уровнями равен
Таким образом, применение уравнения Шредингера к частице в «потенциальной яме» с бесконечно высокими «стенками» приводит к квантованным значениям энергии, в то время как классическая механика на энергию этой частицы никаких ограничений не накладывает.
частица «в потенциальной яме» с бесконечно высокими «стенками» не может иметь энергию
меньшую, чем минимальная энергия, равная
соответствует кинетическая энергия E min»(D p)2/(2 m) = h 2/(2 ml 2). Все остальные уровни (n >1) имеют энергию, превышающую это минимальное значение.
при больших квантовых числах (n >>1) D En/En»2/ n <<1, т. е. соседние уровни расположены тесно: тем теснее, чем больше n. Если n очень велико, то можно говорить о практически непрерывной последовательности уровней и характерная особенность квантовых процессов — дискретность — сглаживается.
8.Прохождение частиц сквозь потенциальный барьер. Туннельный эффект
Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать:
При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него (E < U) и будет двигаться в обратную сторону, т.е. она не может проникнуть через барьер. Для микрочастиц же, даже при E < U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E > U имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи. Прохождение частицы сквозь барьер можно пояснить соотношениемнеопределенностей. Неопределенность импульса на отрезке x = l
составляет Связанная с этим разбросом кинетическая энергия
может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер.
С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является с пецифическим квантовым эффектом.
Строгое квантово-механическое решение задачи о гармоническом осцилляторе приводит еще к одному существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить частицу за пределами дозволенной области
Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта.
Атом водорода
Атом водорода —физическая система,состоящая изатомного ядра,несущегоэлементарный положительный электрический заряд, и электрона, несущего элементарный отрицательный электрический заряд. В состав атомного ядра может входить протон или протон с одним или несколькими нейтронами, образуя изотопы водорода. Электрон преимущественно находится в тонком концентрическом шаровом слое вокруг атомного ядра, образуя электронную оболочку атома. Наиболее вероятный радиус электронной оболочки атома водорода в стабильном состоянии равен боровскому радиусу a0 = 0,529 Å. Атом водорода имеет специальное значение в квантовой механике и релятивистской квантовой механике, поскольку для него проблема двух тел имеет точное или приближенное аналитическое решения. Эти решения применимы для разных изотопов водорода, с соответствующей коррекцией. В квантовой механике атом водорода описывается двухчастичной матрицей плотности или двухчастичной волновой функцией. Также упрощенно рассматривается как электрон в электростатическом поле бесконечно тяжѐлого атомного ядра, не участвующего в
движении (или просто в кулоновском электростатическом потенциале вида 1/ r). В этом случае атом водорода описывается редуцированной одночастичной матрицей плотности или волновой функцией.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 636; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.225.72.200 (0.011 с.) |

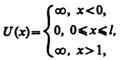
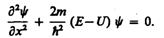

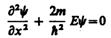
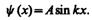
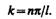


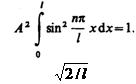

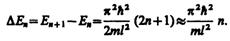
 . Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты D х частицы в «яме» шириной l равна D x = l. Тогда, согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса D p»h/l. Такому разбросу значений импульса
. Наличие отличной от нуля минимальной энергии не случайно и вытекает из соотношения неопределенностей. Неопределенность координаты D х частицы в «яме» шириной l равна D x = l. Тогда, согласно соотношению неопределенностей, импульс не может иметь точное, в данном случае нулевое, значение. Неопределенность импульса D p»h/l. Такому разбросу значений импульса