Условие стационарности состояния атома - квантование момента импульса электрона L.

При движении электрона по круговой орбите радиуса r_n (n = 1,2,3,...) его момент импульса L_n = m_evr_n должен быть кратен постоянной Планка, деленной на 2π, т.е.

Здесь m_e - масса электрона; v - его скорость. Число n называют главным квантовым числом.

Так как, то с учетом этого обозначения условие квантования орбит будет иметь следующий вид:

 

Второй постулат Бора:

Излучение испускается или поглощается в виде квантов энергии при переходе электрона из одного стационарного состояния в другое. Энергия кванта (фотона) равна разности энергий стационарных состояний атома, между которыми происходит переход:

Здесь E_n - энергия стационарного состояния атома до перехода электрона;

E_m - энергия стационарного состояния после квантового перехода электрона. При E_n > E_m фотон с энергией излучается, при E_n < E_m атом поглощает фотон.

Как мы видим, постоянная Планка появляется у Бора дважды: первый раз она определяет стационарные состояния, второй - частоту излучения (или поглощения) при переходе атома из одного стационарного состояния в другое.

Применим условие стационарности состояния атома (4.2.). С помощью этого условия исключим из уравнения (4.1) скорость v. В результате для радиусов стационарных орбит r_n получим:

Радиус первой орбиты (n = 1) называется первым боровским радиусом, его обозначают r₀. Численное значение первого боровского радиуса:

Полная энергия E атома водорода в нашей модели равна сумме кинетической энергии (m_ev²_max)/2 и отрицательной потенциальной энергии взаимодействия электрона с ядром: (-e²)/(4πε₀r), т.е.

Из уравнения движения электрона (4.1) заменим в (4.7) mv²/2 на e²/(8πε₀r), тогда полная энергия атома водорода

Подставив сюда выражение для r_n из (4.5), получим E_n - энергию стационарного состояния атома водорода, зависящую от главного квантового числа n :

Состояние атома водорода при главном квантовом числе n = 1 называется основным состоянием. Численное значение энергии основного состояния атома водорода:

С учетом значения E₁ энергия стационарного состояния E_n имеет простой вид:

 

 

Прохождение частиц сквозь потенциальный барьер. Туннельный эффект

 

Рассмотрим простейший потенциальный барьер прямоугольной формы (рис. 5.4) для одномерного (по оси х) движения частицы. Рис. 5.4 Для потенциального барьера прямоугольной формы высоты U и ширины l можно записать: При данных условиях задачи классическая частица, обладая энергией Е, либо беспрепятственно пройдет над барьером при E > U, либо отразится от него (E < U) и будет двигаться в обратную сторну, т.е. она не может проникнуть через барьер. Для микрочастиц же, даже при E < U, имеется отличная от нуля вероятность, что частица отразится от барьера и будет двигаться в обратную сторону. При E > U имеется также отличная от нуля вероятность, что частица окажется в области x > l, т.е. проникнет сквозь барьер. Такой вывод следует непосредственно из решения уравнения Шредингера, описывающего движение микрочастицы при данных условиях задачи. Уравнение Шредингера для состояний каждой из выделенных областей имеет вид:   , (5.4.1)       . 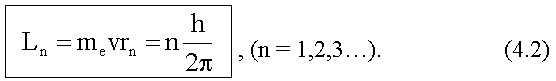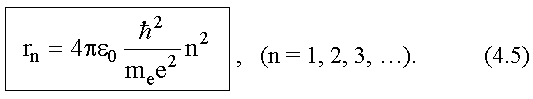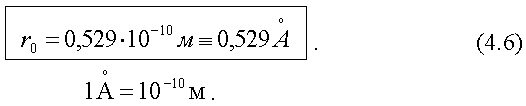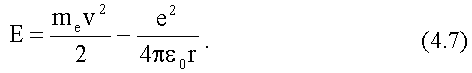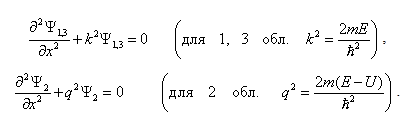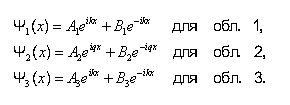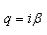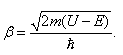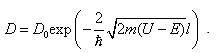(5.4.2)   Общее решение этих дифференциальных уравнений:   (5.4.3)   В данном случае, согласно (5.4.2), – мнимое число, где 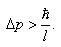Можно показать, что A 1 = 1, B 3 = 0, тогда, учитывая значение q,получим решение уравнения Шредингера для трех областей в следующем виде:   (5.4.4)   В области 2 функция (5.4.4) уже не соответствует плоским волнам, распространяющимся в обе стороны, поскольку показатели степени не мнимые, а действительные. Качественный анализ функций Ψ1(x), Ψ2(x), Ψ3(x) показан на рис. 5.4. Из рисунка следует, что волновая функция не равна нулю и внутри барьера, а в области 3, если барьер не очень широк, будет опять иметь вид волн де Бройля с тем же импульсом, т.е. с той же частотой, но с меньшей амплитудой. Таким образом, квантовая механика приводит к принципиально новому квантовому явлению – туннельному эффекту, в результате которого микрообъект может пройти через барьер. Коэффициент прозрачности для барьера прямоугольной формы. Для барьера произвольной формы. Прохождение частицы сквозь барьер можно пояснить соотношением неопределенностей. Неопределенность импульса на отрезке Δ x = l составляет Связанная с этим разбросом кинетическая энергия может оказаться достаточной для того, чтобы полная энергия оказалась больше потенциальной и частица может пройти через барьер. С классической точки зрения прохождение частицы сквозь потенциальный барьер при E < U невозможно, так как частица, находясь в области барьера, должна была бы обладать отрицательной кинетической энергией. Туннельный эффект является с пецифическим квантовым эффектом. Строгое квантово-механическое решение задачи о гармоническом осцилляторе приводит еще к одному существенному отличию от классического рассмотрения. Оказывается, что можно обнаружить частицу за пределами дозволенной области (рис. 5.5), т.е. за точками 0 и l (рис. 5.1). Рис. 5.5 Это означает, что частица может прибывать там, где ее полная энергия меньше потенциальной энергии. Это оказывается возможным вследствие туннельного эффекта. Основы теории туннельных переходов заложены работами советских ученых Л.И. Мандельштама и М.А. Леонтовича в 1928 г. Туннельное прохождение сквозь потенциальный барьер лежит в основе многих явлений физики твердого тела (например явления в контактном слое на границе двух полупроводников), атомной и ядерной физики (например α-распад, протекание термоядерных реакций).