
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Монохроматические волны. Волновая поверхность, фазовая скорость. Длина волны, групповая скорость и ее физический смысл. Вектор умова.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1) Монохроматическая волна — модель в физике, удобная для теоретического описания явлений волновой природы, означающая, что в спектр волны входит всего одна составляющая по частоте. Стоячая монохроматическая волна — волна, формирующаяся при распространении двух плоских монохроматических электромагнитных волн одинаковой поляризации навстречу друг другу.
2) Волновая поверхность - геометрическое место множества точек, колеблющихся в одинаковой фазе. Луч волны всегда перпендикулярен волновой поверхности. Луч волны - направление распространения волны
Длина волны - путь, пройденный волной за период (или расстояние между точками, колеблющимися с разностью фаз два пи). Волновой процесс периодичен во времени и пространстве (периодичность процесса во времени характеризуется периодом; периодичность процесса в пространстве характеризуется длиной волны).
Фа́зовая ско́рость — скорость перемещения точки, обладающей постоянной фазой колебательного движения, в пространстве вдоль заданного направления. Обычно рассматривают направление, совпадающее с направлением волнового вектора, и фазовой называют скорость, измеренную именно в этом направлении, если противное не указано явно (то есть если явно не указано направление, отличное от направления волнового вектора). Фазовая скорость по направлению волнового вектора совпадает со скоростью движения фазового фронта (поверхности постоянной фазы)
Фазовая скорость вдоль направления, отклонённого от волнового вектора на угол α. Рассматривается монохроматическая плоская волна. Групповая скорость — это величина, характеризующая скорость распространения «группы волн» - то есть более или менее хорошо локализованной квазимонохроматической волны (волны с достаточно узким спектром). Обычно интерпретируется как скорость перемещения максимума амплитудной огибающей квазимонохроматического волнового пакета (или цуга волн). Физический смысл групповой скорости. Групповая скорость во многих важных случаях определяет скорость переноса энергии. Групповая скорость определяется динамикой физической системы, в которой распространяется волна (конкретной среды, конкретного поля итп). В большинстве случаев подразумевается линейность этой системы (точно или приближенно). Для одномерных волн групповая скорость вычисляется из закона дисперсии:
где Групповая скорость волн в пространстве (например, трехмерном или двумерном) определяется градиентом частоты по волновому вектору
или (для трехмерного пространства):
· Замечание: групповая скорость вообще говоря зависит от волнового вектора (в одномерном случае - от волнового числа), то есть вообще говоря различна для разной величины и для разных направлений волнового вектора. 3) Вектор Пойнтинга (также вектор Умова — Пойнтинга) — вектор плотности потока энергии электромагнитного поля, одна из компоненттензора энергии-импульса электромагнитного поля. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
где E и H — векторы напряжённости электрического и магнитного полей соответственно. В случае квазимонохроматических электромагнитных полей, справедливы следующие формулы для усреднённой по периоду комплексной плотности потока энергии[1]:
где E и H — векторы комплексной амплитуды электрического и магнитного полей соответственно. В этом случае чёткий физический смысл имеет только действительная часть комплексного вектора S — это вектор усреднённой за период плотности потока энергии. Физический смысл мнимой части зависит от конкретной задачи. Модуль вектора Пойнтинга равен количеству энергии, переносимой через единичную площадь, нормальную к S, в единицу времени. Своим направлением вектор определяет направление переноса энергии. Поскольку тангенциальные к границе раздела двух сред компоненты E и H непрерывны (см. граничные условия), то нормальная составляющая вектора S непрерывна на границе двух сред. Вектор Пойнтинга и импульс электромагнитного поля В силу симметричности тензора энергии-импульса, все три компоненты вектора пространственной плотности импульса электромагнитного поля равны соответствующим компонентам вектора Пойнтинга, делённым на квадрат скорости света:
В этом соотношении проявляется материальность электромагнитного поля. Поэтому, чтобы узнать импульс электромагнитного поля в той или иной области пространства, достаточно проинтегрировать вектор Пойнтинга по объёму.
1.3 Уравнение плоской монохроматической волны, волновой вектор.
1.4 Волновое уравнение
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1289; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.27.225 (0.006 с.) |



 ,
, — угловая частота,
— угловая частота,  — волновое число.
— волновое число. :
:
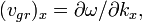


 (в системе СГС),
(в системе СГС), (в системе СИ),
(в системе СИ), (в системе СГС),
(в системе СГС), (в системе СИ),
(в системе СИ), (в системе СИ)
(в системе СИ)





