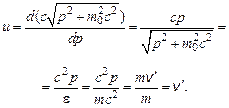Волновая функция и ее физический смысл

В соответствии с гипотезой де Бройля, каждый материальный объект имеет волновые свойства и, следовательно, его можно описать волновой функцией вида y = Ycos (w t – kx).

Циклическая частота w и волновое число k в этом уравнении связаны с энергией и импульсом материальной частицы и могут быть найдены с помощью формул де Бройля.

Но каков смысл y и Y? Какова их природа? Это мгновенное значение и амплитуда чего?

Де Бройль на эти вопросы не дал определенного ответа.

Ученые пытались давать различные объяснения природы волн де Бройля. Сейчас общепринятой является концепция, предложенная немецким физиком Максом Борном. В соответствии с ней физическим смыслом обладает не волновая функция y, а квадрат ее модуля ïyï². Смысл ïyï² в том, что квадрат модуля волновой функции определяет вероятность dp нахождения частицы в некотором элементарном объеме dV:

dp = ïyï² dV.

Вероятность нахождения частицы в некотором конечном объеме V рассчитывается следующим образом:

Если же V – объем всего пространства, в котором находится рассматриваемая частица, то .

Таким образом, квадрат модуля волновой функции представляет собой плотность вероятности нахождения частицы в какой-то точке пространства.

Знание волновой функции не позволяет нам точно определить положение микрочастицы и траекторию ее движения. Можно лишь определить вероятность нахождения частицы в интересующей нас точке пространства.

Это означает, что если волновые свойства частиц проявляют себя, то точное решение даже, казалось бы, простой задачи о расчете траектории движения частицы, невозможно.

Свойства волн де Бройля

Длина волны, свойственной микрочастице, равна l = h/mv = h/p.

Импульс частицы p = h /l = hk /2p, или, в векторной форме,
p = h k /2p, где k – волновой вектор.

Так может быть описана любая частица.

Любая волна характеризуется, в частности, фазовой v и групповой u скоростями. Следовательно, и любая частица должна иметь эти характеристики. Найдем их для некоторой частицы.

Пусть некоторая частица массой m движется в свободном пространстве со скоростью v¢.

По определению фазовая скорость равна отношению циклической частоты волны к ее волновому числу: v = w/ k.

Если умножить и разделить последнее выражение на постоянную Планка, то выражение для расчета фазовой скорости принимает иной вид:

v = ħ w/ ħk = e/ p

(здесь учтено, что полная энергия частицы равна произведению постоянной Планка на циклическую частоту частицы, а ее импульс – произведению волнового числа на постоянную Планка).

С другой стороны, в соответствии со специальной теорией относительности, полная энергия частицы равна произведению ее массы на квадрат скорости света: e = mc².

В свою очередь импульс частицы равен произведению ее массы на скорость частицы: р = mv¢.

Следовательно, фазовая скорость частицы равна

v = e/ p = mc² / mv^¢ = c²/v^¢.

Поскольку скорость движения частиц всегда меньше скорости света в вакууме, постольку фазовая скорость волны де Бройля больше скорости света в вакууме.

Из формулы де Бройля для расчета длины волны частицы легко получить следующее выражение для скорости частицы:
v¢ = h/m l. Подставляя его в формулу для расчета фазовой скорости, получаем

v = c ² m l/ h.

Из последнего выражения видно, что фазовая скорость v прямо пропорциональна длине волны де Бройля l. Следовательно, изменение скорости движения частицы вызывает изменение ее фазовой скорости.

Групповая скорость частицы по определению равна u = d w/ dk.

Умножив и разделив правую часть равенства на постоянную Планка, получаем

и = d (ħ w)/ d (ħk) = d e/ dp.

Из теории относительности известно, что полная энергия частицы e равна

,

где m _о – масса покоя частицы.

Тогда

Это означает, что групповая скорость частицы равна скорости движения частицы.