
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Смысл пси-функции. Стандартные условия.Содержание книги Поиск на нашем сайте
Пси-функция не имеет прямого физического смысла, так как является комплексной величиной. Смысл пси-функции сформулировал Макс Борн: квадрат модуля волновой функции даёт плотность вероятности нахождения частицы в некоторой точке с координатами (x,y,z): Волновая функция должна соответствовать условиям: непрерывности, однозначности, конечности, её производные должны быть непрерывны, она должна быть интегрируема.
12. Принцип суперпозиции. См вопрос 10.
Постулаты квантовой механики. 1. Состояние движения частицы описывается пси-функцией, она удовлетворяет УШ (уравнению Шрёдингера) и стационарным условиям. В соответствии с принципом суперпозиции множество пси-функций, описывающих некоторую механическую систему, образует комплексное линейно-векторное пространство. Каждый вектор этого пространства описывает некоторое состояние системы. Любая суперпозиция векторов этого пространства описывает также состояние системы. Для векторов пространства состояний можно вести скалярное произведение: 2. Каждой динамической переменной в квантовой теории сопоставляется определенный линейный самосопряжённый оператор: 3. При измерении числового значения некоторой динамической переменной q, с определенной вероятностью получается одно из собственных значений оператора
Операторы физических величин. Операторы физической величины определяется исходя из соответствия их выражения в классической механике, принципа соответствия, соотношения неопределенности Гейзенберга и прежде всего в соответствии с требованием совпадения результатов в рамках квантовой формы экспериментальных данных.
1. Оператор координаты: в соответствии с интерпретации пси-функции 2. Оператор импульса найдём исходя из соотношений неопределённости Гейзенберга: 3. Оператор Гамильтона (полной механической энергии) получается в соответствии с принципом классической механики из выражения для полной механической энергии с заменой физических величин их операторами. Оператор Гамильтона – оператор определяющий левую сторону УШ.
Условие одновременной измеримости различных физических переменных. Соотношение неопределённостей. Рассмотрим условия, при которых А и В могут быть одновременно измерены. Пусть в некотором состоянии они имеют определённые значения, тогда их собственные операторы: Соотношение неопределённостей Гейзенберга (
Оператор момента импульса. Момент импульса: Перейдя к полярным координатам мы получим:
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 1458; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.119.158.142 (0.01 с.) |

 ; где P – вероятность, V – объём.
; где P – вероятность, V – объём. .
. . Задача на собственные значения и собственные функции (
. Задача на собственные значения и собственные функции ( ) приводит к вещественным собственным значениям (
) приводит к вещественным собственным значениям ( ). Собственные функции отвечающие различным собственным значениям ортогональны (
). Собственные функции отвечающие различным собственным значениям ортогональны ( ). Совокупность собственных функций образует полную систему, где любая пси-функция может быть представлена как линейная
). Совокупность собственных функций образует полную систему, где любая пси-функция может быть представлена как линейная  .
. . Вероятность получения в опыте значения
. Вероятность получения в опыте значения 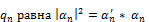 , где
, где  - коэффициент разложения пси-функции по собственным значениям оператора
- коэффициент разложения пси-функции по собственным значениям оператора  . Если пси-функция совпадает с одной из собственных функция, то с вероятностью 1 мы получим при изменении значение
. Если пси-функция совпадает с одной из собственных функция, то с вероятностью 1 мы получим при изменении значение 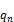 .
. , вероятность того, что частица находится в окрестности точки (x,y,z), среднее значение координаты
, вероятность того, что частица находится в окрестности точки (x,y,z), среднее значение координаты  в качестве оператора координаты выбираем
в качестве оператора координаты выбираем  .
.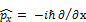 , задача на собственные значения функции
, задача на собственные значения функции  .
.  -собственная функция, отвечающая за собственное значение импульса. Таким образом, собственная функция оператора импульса частицы с энергией и импульсом, сопоставляет волну частоты
-собственная функция, отвечающая за собственное значение импульса. Таким образом, собственная функция оператора импульса частицы с энергией и импульсом, сопоставляет волну частоты  и волновым числом
и волновым числом  .
. :
:  . Предположим, что
. Предположим, что 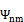 образуют полную систему собственных векторов, тогда для произвольного вектора состояния:
образуют полную систему собственных векторов, тогда для произвольного вектора состояния:  . В силу произвольности
. В силу произвольности  получаем операторное равенство:
получаем операторное равенство: 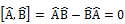 . Другими словами, наблюдаемые должны коммутировать.
. Другими словами, наблюдаемые должны коммутировать. ) показывает, что между точностью, с которой одновременно может быть установлено положение частицы, и точностью её импульса существует определённое соотношение. (Соотношение неопределённостей Гейзенберга помогает определить вероятность нахождения частицы в данной точке пространства.)
) показывает, что между точностью, с которой одновременно может быть установлено положение частицы, и точностью её импульса существует определённое соотношение. (Соотношение неопределённостей Гейзенберга помогает определить вероятность нахождения частицы в данной точке пространства.) , оператор момента импульса:
, оператор момента импульса:  =-
=-  . Компоненты оператора момента импульса:
. Компоненты оператора момента импульса:  =-
=-  . Вследствие коммутативности оператора, частица не может иметь определённые значения 2х, 3х компонентов момента импульса, при этом можно одновременно измерить и получить определённые значения квадрата момента импульса.
. Вследствие коммутативности оператора, частица не может иметь определённые значения 2х, 3х компонентов момента импульса, при этом можно одновременно измерить и получить определённые значения квадрата момента импульса. , где
, где  ). В силу стандартных условий проекция момента импульса может принимать только дискретный набор значений (Lz=m
). В силу стандартных условий проекция момента импульса может принимать только дискретный набор значений (Lz=m 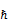 , m =
, m =  …). Квадрат момента импульса:
…). Квадрат момента импульса:  , l =
, l =  .
.


