
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Частица в бесконечно глубокойСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Потенциальной яме Потенциальной ямой называют область пространства, в которой потенциальная энергия меньше, чем в соседних областях.
В такой яме частица может двигаться вдоль оси х от точки х = 0 до точки х = L. В области х < 0 и х > L частица проникнуть не может. График зависимости потенциальной энергии от координаты изображен на рисунке (происхождение названия «потенциальная яма» связано с видом графика зависимости U (x)). Классическая частица в такой ситуации может двигаться внутри ямы совершенно свободно, но за стенки ямы проникнуть не может. Ее скорость в яме может быть любой. В частности, энергия может равняться нулю, т.е. частица может просто покоиться в какой либо точке с координатой L > x > 0. Если скорость классической частицы отлична от нуля, то частица должна совершать колебания между точками х = 0 и x = L – долетев до какой-либо стенки ямы, частица отразится от нее и полетит в противоположную сторону. Поведение квантовой частицы, в отличие от классической, более сложно, хотя есть и некоторое сходство. Сходство заключается в том, что в такой ситуации квантовая частица тоже не может проникнуть за стенки потенциальной ямы (так как они бесконечно высоки). На языке квантовой механики это означает, что y(0) = 0, y(L) = 0. Все остальные особенности поведения квантовой частицы можно найти, решив уравнение Шрёдингера для этой ситуации. Поскольку яма бесконечно глубока, уравнение записываем лишь для области 0 < x < L. Уравнение здесь имеет вид
Общее решение уравнения выглядит следующим образом:
где Полная волновая функция
т.е. частица в этой ситуации представлена в виде суперпозиции двух встречных бегущих волн. Найдем связь амплитуд падающей А и отраженной В волн. Так как y(0) = 0, то Aeik 0+ Be - ik 0 = A + B = 0, A = – B и y = A (ikx – e-ikx). Поскольку eikx = cos kx + i sin kx, выражение для волновой функции можно привести к виду y = 2 iA sin kx = C sin kx. Так как y(L) = 0, C sin kL = 0. Поскольку С ¹ 0, нулю должен равняться синус: sin kL = 0. Отсюда следует, что kL = n p, т.е. k не может принимать произвольные значения, ему разрешены лишь значения из ряда Это означает, что волновая функция может иметь лишь такой вид, при котором на ширине ямы укладывается целое число полуволн де Бройля: Как известно, наложение встречных волн, отвечающих такому условию, вызывает возникновение стоячей волны. Следовательно, в бесконечно глубокой потенциальной яме волновая функция может иметь такой вид, при котором на ширине ямы возникают стоячие волны де Бройля. Таким образом, волновая функция, описывающая квантовую частицу в бесконечно глубокой прямоугольной потенциальной яме, имеет следующий вид:
По условию частица обязательно находится внутри потенциальной ямы. Это значит, что
Тогда
Учитывая, что Поэтому функция y(x) принимает окончательный вид
Отметим еще одну важную особенность. Поскольку Таким образом, квантовая частица в яме не может «лежать на дне» – значение энергии E = 0 запрещено для квантовой частицы. Квантовая частица в такой яме может существовать лишь в движении, причем в движении, отвечающем волновому числу
Вид волновых функций, соответствующих разрешенным состояниям, схематически изображен на рисунке. Итак, квантовой частице в потенциальной яме разрешены лишь такие состояния, для которых на ширине ямы укладывается целое число полуволн де Бройля (т.е. разрешены состояния, для которых возможно возникновение стоячей волны де Бройля). Как видно из рисунка, вероятность обнаружения частицы в разных точках ямы различна (у классической частицы она одинакова). Вероятность обнаружения частицы в той или иной точке зависит от координаты. В состоянии с минимальной возможной энергией наиболее вероятно обнаружить частицу в центре ямы и практически невероятно обнаружить частицу у краев ямы. Если частица имеет более высокую энергию (Е 2, Е 3 и т.д.), то вероятность обнаружения частицы в нескольких точках ямы максимальна. Между этими точками обязательно имеются такие, в которых квантовая частица не будет обнаружена никогда (точки, в которых квадрат модуля волновой функции равен нулю). Квантовая частица может находиться на дискретных энергетических уровнях, разделенных интервалом Величина интервала зависит от массы частицы m, ширины потенциальной ямы L, значения квантового числа n. Анализ выражения для расчета D En показывает, что интервал между соседними разрешенными значениями энергии квантовой частицы увеличивается по мере увеличения номера энергетического уровня n. Чем больше масса квантовой частицы, тем ближе разрешенные уровни энергии частицы, тем ближе к непрерывному (классическому) спектр разрешенных значений энергии частицы. С уменьшением ширины ямы дискретность энергетических уровней возрастает. Следовательно, чем точнее задается положение частицы, тем заметнее ее квантовый характер. Следовательно, различия между квантовой и классической механикой становятся все менее заметными по мере увеличения массы частиц и ширины потенциальных ям, ограничивающих свободу перемещения частиц. Таким образом, квантовая механика ни в коей мере не перечеркивает классическую механику.
|
||||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 3730; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.224.44.207 (0.007 с.) |

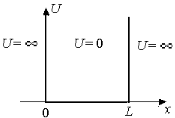 Пусть частица находится в одномерной бесконечно глубокой потенциальной яме.
Пусть частица находится в одномерной бесконечно глубокой потенциальной яме.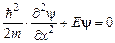 .
.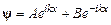 ,
, .
.
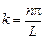 , где n = 1, 2, 3...
, где n = 1, 2, 3...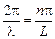 и
и 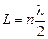 .
.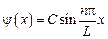 .
.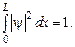
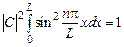 .
.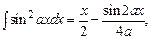 мы можем получить, что
мы можем получить, что  .
. .
.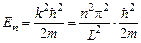 , где n = 1, 2, 3...
, где n = 1, 2, 3...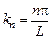 и энергии
и энергии 

 .
.


