
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые и бесконечно большие функцииСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Определение. Функция a(x) называется бесконечно малой при x ® x 0или в точке Определение. Функция f (x) называется бесконечно большой в точке Определение. Функция f (x) называется ограниченной на некотором множестве X Ì D (f), если существует такое число M > 0, что для любого x Î X выполняется неравенство | f (x)| < M. 2. Теорема (о связи между бесконечно малой функцией в точке x0 и бесконечно большой функцией в точке x0) Если функция f (x ) является бесконечно большой в точке Теорема о разложении функции, имеющей предел на постоянную и бесконечно малую функцию. Теорема. Если функция ƒ(х) имеем предел, равный А, то ее можно представить как сумму числа А и бесконечно малой функции α(х), т. е. если limƒ(х)=А, при Х→Хо то ƒ(х)=А+а(х). Теоремы о пределах. 1) 2) 3) 4) 5)
Первый и второй замечательные пределы. Сравнение бесконечно малых функций. Эквивалентные функции. Первый замечательный предел: Предел функции Второй замечательный предел: Предел функции
Сравнение бесконечно малых функций: α(x), β(x) - бесконечно малые функции
Эквивалентные функции:
Непрерывность функции в точке и на отрезке. Точки разрыва, их классификация. Теоремы о непрерывных функциях. Непрерывность функции в точке и на промежутке Определение. Функция f (x) называется непрерывной в точке x 0ÎD(f),если она определена в некоторой окрестности точки x 0 и предел f (x) в точке x 0 равен значению функции в этой точке. Определение. Функция f (x) называется непрерывной на промежутке, если она непрерывна в каждой точке этого промежутка. Точки разрыва функции и их классификация Определение. Точка x 0 называется точкой разрыва функции f (x), если в этой точке функция либо не определена, либо определена, но нарушено хотя бы одно из условий определения 3 непрерывности f (x). Определение. Точка x 0 называется точкой устранимого разрыва функции f (x), если предел функции в этой точке существует, но f (x) в точке x 0 либо не определена, либо имеет значение f (x 0), не совпадающее с найденным пределом: f (x 0 – 0) = f (x 0 + 0) ¹ f (x 0). Определение. Точка x 0 называется точкой разрыва первого рода функции f (x) (разрыв типа «скачка»), если в этой точке функция имеет конечные, но не равные между собой правый и левый пределы, т.е. f (x 0 – 0) ¹ f (x 0 + 0). Определение. Точка x 0 называется точкой разрыва второго рода функции f (x), если в этой точке функция не имеет хотя бы одного из односторонних пределов или хотя бы один из односторонних пределов бесконечен. Теоремы о непрерывных функциях Теорема. Если функции f (x) и g (x) непрерывны в точке x 0 , то функции с × f (x) (c =const), f (x) ± g (x), f (x) × g (x) и Теорема. Если функция u = u (x) непрерывна в точке x 0 и функция y = f (u) непрерывна в точке u 0 = u (x 0), то сложная функция y = f (u (x)) непрерывна в точке x 0. Теорема. Все элементарные функции непрерывны в каждой точке области их определения. 5. Производная функции, её механическая интерпретация. Связь между непрерывностью и дифференцируемостью функции. Дифференциал функции, его связь с производной. Геометрический смысл производной и дифференциала. Уравнения касательной и нормали к кривой. Определение производной, её геометрический и механический смысл 2. Определение 1. Приращением функции 3. Определение 2. Производной функции 4.
|
||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-18; просмотров: 1543; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.223.136 (0.01 с.) |

 ,если пределa(x)при x®
,если пределa(x)при x®  .
. удовлетворяющего неравенству
удовлетворяющего неравенству  , выполняется неравенство | f (x)| > M.
, выполняется неравенство | f (x)| > M. является бесконечно малой в точке
является бесконечно малой в точке 
 т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).
т. е. |ƒ(х)-А-0|<ε. Это означает, что функция ƒ(х)-А имеет предел, равный нулю, т. е. является б.м.ф., которую обозначим через α(х): ƒ(х)-А=α(х). Отсюда ƒ(х)=А+α(х).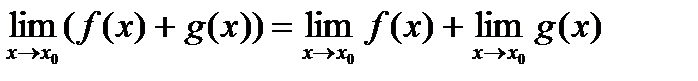

 , если g(x)≠0 в δ(x0)
, если g(x)≠0 в δ(x0)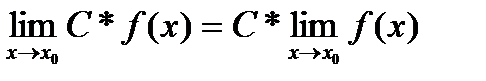 ;
; 

 в точке
в точке  существует и равен 1, т.е.
существует и равен 1, т.е. 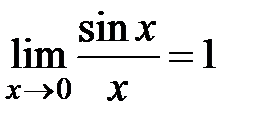 .
. при x
при x  существует и равен числу e, т.е.
существует и равен числу e, т.е. .
.


 - α
- α
 -1 ~ α
-1 ~ α
 -1 ~ α lna
-1 ~ α lna
 ~
~ 
 -1 ~
-1 ~ 
 -1 ~
-1 ~ 
 (если g (x) ¹ 0) также непрерывны в точке x 0.
(если g (x) ¹ 0) также непрерывны в точке x 0. называется разность f (x +D x) – f (x). Приращение функции
называется разность f (x +D x) – f (x). Приращение функции  называется предел отношения приращения функции D y к приращению аргумента D x, если приращение аргумента D x стремится к нулю и этот предел существует. Производную функции
называется предел отношения приращения функции D y к приращению аргумента D x, если приращение аргумента D x стремится к нулю и этот предел существует. Производную функции  или
или  . Поэтому можно записать:
. Поэтому можно записать:



