
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Бесконечно малые функции (б. м. ф.)Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Функция называется б. м. ф., если Свойства б. м. ф.: 1. Сумма, состоящая из конечного числа (слагаемых) бесконечно малых есть бесконечно малая функция 2. Произведение бесконечно малой функции на функцию ограниченную есть бесконечно малая функция. Функцию f(x) называют ограниченной на множестве Е, если существует такая константа М, что для любого х Î Е выполняется Функция, имеющая предел при х ® а, - ограничена в окрестности точки а. Следовательно, произведение б. м. ф. на функцию, имеющую предел, есть б. м. ф. Произведение бесконечно малых функций есть бесконечно малая функция. Бесконечно большая функция Пусть Если функция f(x) - бесконечно большая и f(x)¹ 0 в окрестности точки а, то Как понимать х ® + ¥, х ® - ¥ и х ® ¥? Будем говорить, что х ® + ¥, если х может стать больше любого наперед заданного числа, х ® - ¥, если х может стать меньше любого наперед заданного числа, х ® ¥, если абсолютная величина х может стать больше любого наперед заданного числа. Свойства пределов: 1. Предел суммы функций, состоящий из конечного числа слагаемых, равен сумме пределов. 2. Предел произведения равен произведению пределов. 3. Предел частного равен частному пределов, если предел знаменателя неравен нулю. Например, если а) б) в) Неопределенности. Неопределенность Рассмотрим вычисление х2-1=(х-1)*(х+1), и подставим в выражение Рассмотрим вычисление
Замечательные пределы и следствия из них. Первый замечательный предел Первым замечательным пределом называется выражение Следствия из первого замечательного предела: 1) Второй замечательный предел Вторым замечательным пределом называется выражение
Следствия их второго замечательного предела:
ЗАДАЧА № 6 Вычислить пределы:
1. 2. 3. 4.
Производная функции Производной функции f(x) называется предел Для производной используют и другие обозначения - Правила дифференцирования Пусть U и V - дифференцируемые функции, т. е. для них существуют производные, с - константа. 1. (с)¢ = 0; 2. (U + V)¢ = U¢ + V¢; 3. (UV)¢ = U¢V + UV¢; 4. (CU)¢ = CU¢; 5. 6. Пусть f(x) - дифференцируемая функция, тогда Производные основных элементарных функций
Производные высших порядков Производной второго порядка называется производная от производной, производной третьего порядка называется производная от производной второго порядка и т. д. Производная неявной функции Говорят, что функция y = f(x) задана неявно, если она задана в виде уравнения f(x, y) = 0, неразрешенного относительно у. Например, х2 + у2 = ху. Для того, чтобы вычислить а) дифференцируют левую и правую части уравнения по переменной х, при этом переменную у считают функцией от х, например, (х2 + у2)х¢ = (ху)х¢; 2= + 2у * у¢ = у + ху¢. б) решают полученное уравнение относительно у¢, например, 2у * у¢ - х у¢ = у + 2х; у¢ (2у - х) = у + 2х; Производная функции, заданной параметрически Говорят, что функция у = f(x) задана параметрически, если она задана в виде системы уравнений: Например, При дифференцировании функции, заданной параметрически, используют формулу Геометрический смысл производной: производная - тангенс угла наклона касательной:
Механический смысл производной: производная - мгновенная скорость тела в заданный момент времени. ДИФФЕРЕНЦИАЛ ФУНУЦИИ Дифференциалом функции y = f(x) (обозначается dy, df(x)) называется главная часть приращения функции, линейная относительно приращения аргумента. Если у функции y = f(x) существует неравная нулю производная, то d f(x) = f¢(x)Dx. Например, Основные свойства дифференциала:
ЗАДАЧА № 7 1. Вычислить производную: 2. Вычислить производную второго порядка: 3. Найти производную функции, заданной неявно: 4. Найти производную функции, заданной параметрически: 1.
2.
3.
4. ИССЛЕДОВАНИЕ ФУНКЦИИ. Монотонность функции Функция называется возрастающей (убывающей), если из х1 < х2 следует, что f(x1) < f(x2) (f(x1) > f(x2)). Достаточное условие возрастания (убывания) функции: если для любого х Î (а, в) f¢(x) > 0 (f¢(x) < 0), то f(x) возрастает (убывает) на (а, в). Экстремальные точки функции Точка х 0 называется точкой максимума (минимума) функции у = f(x), если существует d>0, такое, что из х Î (х0 -d, х0 +d), х¹ х 0 следует f(x)< f(x0) (f(x) > (x0)).
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 591; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.009 с.) |

 Например,
Например, 

 .
.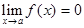 и
и 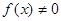 в окрестности точки а, тогда функция
в окрестности точки а, тогда функция  называется бесконечно большой функцией. Обозначается
называется бесконечно большой функцией. Обозначается 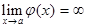 .
.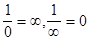 .
.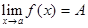 и
и 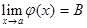 , то
, то ;
;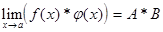 ;
; .
.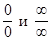
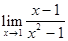 . Подставим вместо х предельное значение 1:
. Подставим вместо х предельное значение 1: 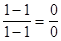 . Эта ситуация называется неопределенностью
. Эта ситуация называется неопределенностью 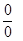 . Для того, чтобы вычислить
. Для того, чтобы вычислить 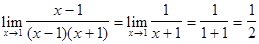 .
.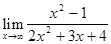 . При стремлении х к бесконечности, многочлены в числителе и знаменателе стремятся к бесконечности, и возникает неопределенность вида
. При стремлении х к бесконечности, многочлены в числителе и знаменателе стремятся к бесконечности, и возникает неопределенность вида 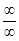 . Для того, чтобы вычислить
. Для того, чтобы вычислить 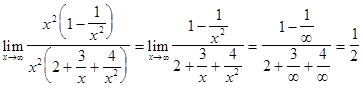 .
. 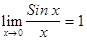 .
.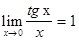 ; 2)
; 2) 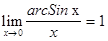 ; 3)
; 3) 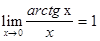 .
.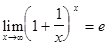 или
или 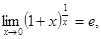 где е - математическая константа, приблизительно равна 2, 71.
где е - математическая константа, приблизительно равна 2, 71.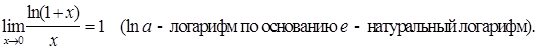
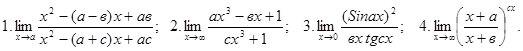
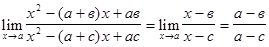 ;
;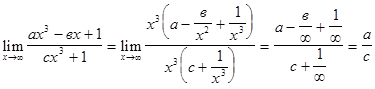 ;
;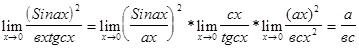 ;
;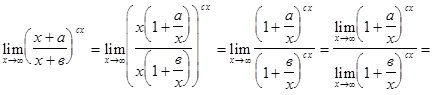
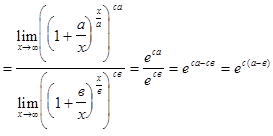 .
.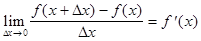 .
.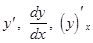 .
.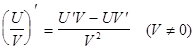 ;
;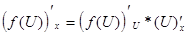 .
.
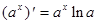











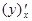 поступают следующим образом:
поступают следующим образом: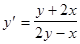 .
. , t - параметр.
, t - параметр.
 .
.


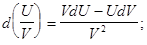
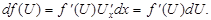
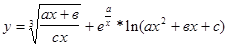 ;
;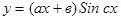 ;
; ;
;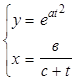 ;
;
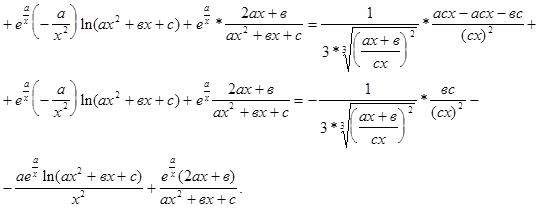
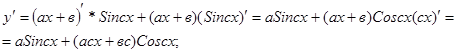
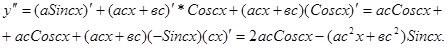
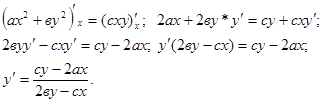
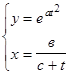 Þ
Þ 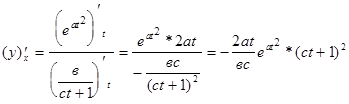 .
.


