
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Достаточное условие экстремальности точкиСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте Если в точке х 0: а) производная равна нулю или не существует; б) при переходе через точку изменяется знак производной, то точка х 0 - экстремальная. Если производная изменяет знак с плюса на минус, то точка х0 - точка максимума, если с минуса на плюс, то х0 - точка минимума. Выпуклость, вогнутость функции. Точки перегиба Функция у = f(x) называется выпуклой на (а, в), если для любых точек х1 и х2, принадлежащих интервалу (а, в), и любого a Î (0, 1) выполняется неравенство: Функция у = f(x) называется вогнутой на (а, в), если для любых точек х1 и х2 Î (а, в) и любого a Î (0, 1) выполняется неравенство:
Точка х0 называется точкой перегиба, если она отделяет интервал, на котором функция выпукла, от интервала, на котором функция вогнута. Достаточное условие выпуклости (вогнутости) функции: если вторая производная Достаточное условие для точки перегиба: если в точке х0 вторая производная Асимптоты Пусть точка А, перемещаясь по графику функции устремляется в бесконечность, если при этом расстояние между точкой и некоторой прямой стремятся к нулю, то эта прямая называется асимптотой. Вертикальная асимптота.
Для того, чтобы прямая х = а была вертикальной асимптотой, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий: а) Наклонная асимптота
Условия существования наклонной асимптоты Для того, чтобы прямая у = kх + в была наклонной асимптотой, необходимо и достаточно, чтобы выполнялось хотя бы одно из условий: а) При этом
План исследования функции: 1. Область определения функции. 2. Четность (нечетность) функции. 3. Периодичность. 4. Точки пересечения с осями. 5. Монотонность. Экстремальные точки. 6. Выпуклость (вогнутость) функции. Точки перегиба. 7. Асимптоты. ЗАДАЧА № 8 Провести полное исследование функции 1. Область определения: (х - с)2 - 3 ¹ 0; (х - с)2 ¹ 3; х - с ¹ ± Ö3. Следовательно, 2. Точки пересечения с осями: а) ось ОУ: б) ось ОХ: y = 0 Поскольку решение кубического уравнения с параметрами выходит за пределы курса, то находить точки пересечения с осью ОХ не будем. 3. Четность, нечетность функции: Рассмотрим 4. Функция не является периодической. 5. Монотонность, экстремальные точки: Находим производную: Приравниваем производную к нулю: Отсюда находим три решения: х1 = с - 3, х2 = с, х3 = с + 3. Составляем таблицу:
6. Точки перегиба. Выпуклость, вогнутость функции. Находим вторую производную: Приравниваем ее к нулю: 6а(х - с)((х - с)2 + 9)=0; ((х - с)2 - 3)3 ¹ 0. Получаем единственное решение х = с и составляем таблицу:
7. Асимптоты. Вертикальные. Поскольку знаменатель обращается в нуль при х = c - √3 и х = c + √3, а числитель нет, то вертикальные прямые х = c - √3 и х = c + √3 - вертикальные асимптоты. Наклонные.
ПОЯСНЕНИЕ Вариант выбирается по двум последним цифрам зачетки: - если последние две цифры образуют число, меньшее пятидесяти, то номер варианта совпадает с этим числом. Например, последние две цифры 48 – вариант 48; - если последние две цифры образуют число, большее или равное пятидесяти, то номер варианта равен разности между этим числом и пятьдесят. Например, последние две цифры 61 - вариант 11. Таблица
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 538; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.007 с.) |

 .
. .
. на интервале (а, в), то функция у = f(x) - выпукла (вогнута) на (а, в).
на интервале (а, в), то функция у = f(x) - выпукла (вогнута) на (а, в). или не существует и при переходе через точку х0 изменяет свой знак, то точка х0 - точка перегиба.
или не существует и при переходе через точку х0 изменяет свой знак, то точка х0 - точка перегиба. 
 б)
б) 

 б)
б)  .
. .
.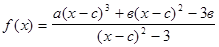 и построить график.
и построить график.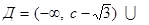
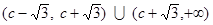 .
.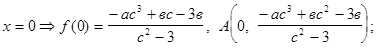
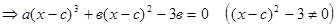 .
.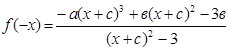 и убедимся, что
и убедимся, что 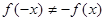 , функция не является нечетной, и
, функция не является нечетной, и 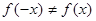 - функция не является четной.
- функция не является четной.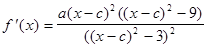 .
.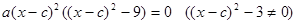 .
.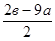
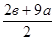
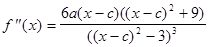 .
.
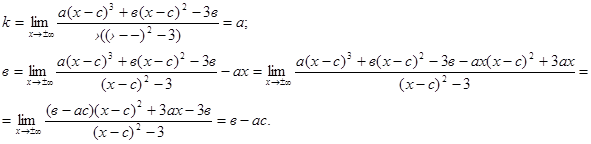 Отсюда, прямая у = ах + (в - ас) - наклонная асимптота.
Отсюда, прямая у = ах + (в - ас) - наклонная асимптота.


