
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление объема тела вращенияСодержание книги Похожие статьи вашей тематики
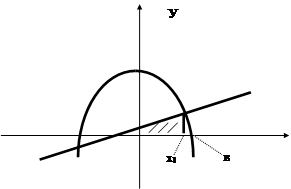
Поиск на нашем сайте Рассмотрим криволинейную трапецию, ограниченную кривой y = f(x) и прямыми у = 0, х = в. Пусть эта трапеция вращается вокруг оси Ох. Тогда объем тела вращения вычисляется по формуле Если фигура, ограниченная кривыми y = f1(x); y = f2(x) (0 ≤ f1(x) ≤ f2(x)) и прямыми х = а, х = в, вращается вокруг оси Ох, то объем тела вращения Рассмотрим криволинейную трапецию х = j(у), х = 0, у = 1, у = d. Объем тела вращения, полученного путем вращения этой трапеции вокруг оси Оу, ЗАДАЧА № 21 Найти объем тела вращения
ДВОЙНОЙ ИНТЕГРАЛ ДВОЙНОЙ ИНТЕГРАЛ В ПРЯМОУГОЛЬНЫХ КООРДИНАТАХ Пусть функция f(x,y) определена и непрерывна в ограниченной замкнутой области Д плоскости хОу. Разобьем область Д произвольным образом на n элементарных областей, имеющих площади
Такая сумма называется интегральной суммой. Определение: Предел интегральной суммы при условии, что число элементарных областей n ® 1) ни от способа разбиения области Д на элементарные области; 2) ни от способа выбора в них точек Рi
Если f(x, y) > 0 в области Д, то двойной интеграл Свойства двойного интеграла аналогичны свойствам определенного интеграла. ВЫЧИСЛЕНИЕ ДВОЙНОГО ИНТЕГРАЛА Существуют два основных вида области интегрирования: 1.Область интегрирования Д ограничена слева и справа прямыми х = а, х = в (а < в), а снизу и сверху - непрерывными кривыми у = j1(х) и у =j2(х) (j1(х) £ j2(х)), каждая из которых пересекается прямой, параллельной оси Оу, только в одной точке (рис. 1).
Рис. 1
Рис. 2 Вычисление двойного интеграла сводится к двукратному интегрированию
Интеграл Для того, чтобы поставить пределы внутреннего интеграла, надо посмотреть на изменение у вдоль вектора 2. Пусть область интегрирования Д ограничена снизу и сверху прямыми у = с, у = d (с < d), а слева и справа - непрерывными кривыми х = Y1(у), х = Y2(у) (Y1 (у) £ Y1 (у)), каждая из которых пересекается горизонтальной прямой только в одной точке (рис. 2). Тогда двойной интеграл по такой области вычисляется по формуле
причем сначала вычисляется внутренний интеграл, ЗАДАЧА № 22 Вычислить повторные интегралы 1.

ЗАДАЧА № 23 Вычислить следующие двойные интегралы по области Д, ограниченные линиями 1.

2.
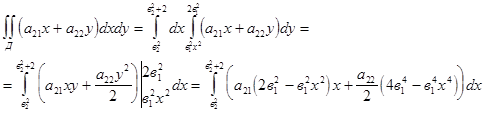
=
ВЫЧИСЛЕНИЕ ПЛОЩАДИ ПЛОСКОЙ ФИГУРЫ Площадь плоской фигуры, ограниченной областью Д, определяется по формуле Если область Д определена неравенствами а £ х £ в, j1(х) £ у £ j2(х), то двойной интеграл вычисляется по формуле Если область Д в полярных координатах определена неравенствами a £ j £ b, p1(j) £ r £ p2(j), то площадь ЗАДАЧА № 24 С помощью двойного интеграла вычислить площадь фигур 1. 1.
ВЫЧИСЛЕНИЕ ОБЪЕМА ТЕЛА Объем цилиндрического тела, ограниченного сверху непрерывной поверхностью z = f(x,y), снизу плоскостью z = 0, сбоку - цилиндрической поверхностью, вырезающей на плоскости хОу область Д, вычисляется по формуле:
ЗАДАЧА № 25 Вычислить объем тела, ограниченного заданными поверхностями 1. Проекция тела на плоскость ХОУ:
Перейдем к полярным координатам:
ПОЯСНЕНИЕ Номер варианта в задачах 9 - 25 совпадает с последней цифрой номера зачетной книжки.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ РОСТОВСКИЙ ГОСУДАРСТВЕННЫЙ СТРОИТЕЛЬНЫЙ УНИВЕРСИТЕТ КАФЕДРА «ИНФОРМАЦИОННЫЕ СИСТЕМЫ В СТРОИТЕЛЬСТВЕ» КОНТРОЛЬНАЯ РАБОТА ПО ВЫСШЕЙ МАТЕМАТИКЕ № 1 Студента(ки) группы _________________________________________________
(Фамилия, имя, отчество)
«______» ___________ 200___ г. (дата сдачи)
№ ____________
«______» ___________ 200__ г.
Шифр № _________________
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 736; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.005 с.) |

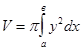 .
. .
. .
.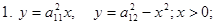
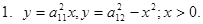

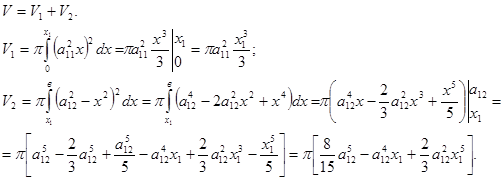
 S1 ,
S1 ,  .
. и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит:
и наибольший диаметр max dk ® 0, называется двойным интегралом от функции f(x, y) по области Д, если этот предел существует и не зависит: .
. равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).
равен объему цилиндрического тела, ограниченного сверху поверхностью z = f(x, y), сбоку - образующими параллельные оси Оz, а снизу - областью Д (лежащей на плоскости хОу).








 .
. называется внутренним. В нем х считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х.
называется внутренним. В нем х считается постоянной. Этот интеграл вычисляется в первую очередь. А потом вычисляется внешний интеграл по переменной х. от точки входа вектора в область Д (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х.
от точки входа вектора в область Д (нижний предел) до точки выхода вектора из области Д (верхний предел). Пределы внешнего интеграла всегда постоянны и показывают пределы изменения переменной х. ,
, , в котором у считается постоянной.
, в котором у считается постоянной. .
. .
. ; 2.
; 2.  .
. 1.
1.  ;
;  .
.

 ;
;  ;
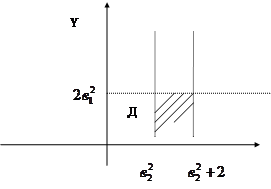
;



 .
.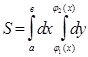 .
.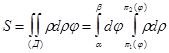 .
.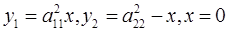 .
. ;
;



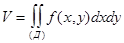 .
. ;
;
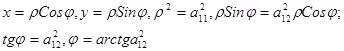
 .
.


