Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вращение твёрдого тела вокруг неподвижной осиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Вращением твёрдого тела вокруг неподвижной оси называется такое его движение, при котором две точки тела остаются неподвижными в течение всего времени движения. При этом также остаются неподвижными все точки тела, расположенные на прямой, проходящей через его неподвижные точки. Эта прямая называется осью вращения тела.
Положение плоскости Положение тела относительно выбранной системы отсчета однозначно определяется в любой момент времени, если задано уравнение
Рис. 4-4
У тела, совершающего вращение вокруг неподвижной оси, одна степень свободы, так как его положение определяется заданием только одного параметра – угла Угол Для характеристики вращательного движения твердого тела вокруг неподвижной оси введём понятия угловой скорости и углового ускорения. Алгебраической угловой скоростью тела в какой-либо момент времени называется первая производная по времени от угла поворота в этот момент, то есть Угловая скорость является положительной величиной при вращении тела против часовой стрелки, так как угол поворота возрастает с течением времени, и отрицательной – при вращении тела по часовой стрелке, потому что угол поворота при этом убывает. Размерность угловой скорости по определению: В технике угловая скорость – это частота вращения, выраженная в оборотах в минуту. За одну минуту тело повернётся на угол
Алгебраическим угловым ускорением тела называется первая производная по времени от угловой скорости, то есть вторая производная от угла поворота т.е. Размерность углового ускорения по определению: Введем понятия векторов угловой скорости и углового ускорения тела.
Рис. 4-5
Если При Если Если Угловую скорость и угловое ускорение на рисунках изображают дуговыми стрелками вокруг оси вращения (если нельзя изобразить вектора). Дуговая стрелка для угловой скорости указывает направление вращения тела, а дуговая стрелка для углового ускорения – направление, в котором увеличивается алгебраическая угловая скорость. Для ускоренного вращения дуговые стрелки для угловой скорости и углового ускорения имеют одинаковые направления, для замедленного их направления противоположны.
Частные случаи вращения твердого тела Равномерное вращение Вращение называется равномерным, если его угловая скорость постоянна, т.е. Так как
Равнопеременное вращение Вращение называется равноускоренным, если его угловое ускорение постоянно и больше нуля, т.е. Вращение называется равнозамедленным, если его угловое ускорение постоянно и меньше нуля, т.е. Так как
далее
или 11.Ск-ть и уск тверд тела…
|
||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 672; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.006 с.) |

 Пусть точки A и B неподвижны. Вдоль оси вращения направим ось
Пусть точки A и B неподвижны. Вдоль оси вращения направим ось  . Через ось вращения проведём неподвижную плоскость
. Через ось вращения проведём неподвижную плоскость  и подвижную
и подвижную  , скреплённую с вращающимся телом (при
, скреплённую с вращающимся телом (при 
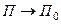 ).
). . Угол
. Угол 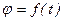 , где
, где  - любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.
- любая дважды дифференцируемая функция времени. Это уравнение называется уравнением вращения твёрдого тела вокруг неподвижной оси.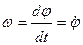 .
.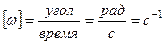
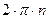 , где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим
, где n - число оборотов в минуту. Разделив этот угол на число секунд в минуте, получим


 и
и 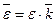 , где
, где  - единичный вектор оси вращения. Векторы
- единичный вектор оси вращения. Векторы  и
и  можно изображать в любых точках оси вращения, они являются скользящими векторами.
можно изображать в любых точках оси вращения, они являются скользящими векторами.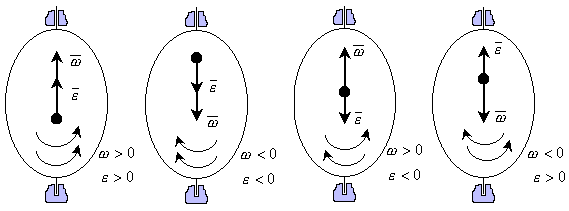
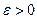 при
при  , то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов
, то алгебраическая угловая скорость возрастает с течением времени и, следовательно, тело вращается ускоренно в рассматриваемый момент времени в положительную сторону. Направление векторов  .
. и
и  тело вращается ускоренно в отрицательную сторону. Направление векторов
тело вращается ускоренно в отрицательную сторону. Направление векторов  .
.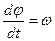 , то
, то  . Начальные условия:
. Начальные условия: 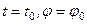 , то после интегрирования получим
, то после интегрирования получим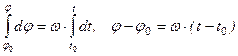 или
или 

 .
. .
. , то
, то  . Начальные условия:
. Начальные условия:  , то после интегрирования получим
, то после интегрирования получим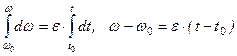 или
или 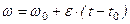

 и после интегрирования,
и после интегрирования,