
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сферическое движение. Углы Эйлера. Угловая скорость и угловое ускорение при сферическом движении твёрдого тела.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сферическое движение (движение твёрдого тела вокруг неподвижной точки) — движение абсолютно твёрдого тела, при котором оно имеет одну неподвижную точку. При движении вокруг неподвижной точки О каждая из точек твёрдого тела описывает в пространстве сферическую поверхность, центром которой является точка О. При описании законов сферического движения принято пользоваться координатами, получившими название углов Эйлера:
Угловая скорость — векторная физическая величина, характеризующая скорость вращения тела. Вектор угловой скорости по величине равен углу поворота тела в единицу времени:
Угловое ускорение — псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости твёрдого тела. При вращении тела вокруг неподвижной оси, угловое ускорение по модулю равно
Определение скоростей и ускорений точек твёрдого тела, совершающего сферическое движение. Скорости точек твёрдого тела в сферическом движении определяют по формуле Эйлера: Модуль скорости равен: Ускорение точки в сферическом движении равно геометрической сумме вращательного и осестремительного ускорения.
Общий случай движения свободного твёрдого тела, Уравнения движения. Скорость и ускорение точки. Скорость любой точки твёрдого тела равна геометрической сумме скорости полюса и скорости это точки во вращательном движении тела вокруг полюса.
Ускорение точки свободного твёрдого тела равно геометрической сумме ускорения полюса и ускорения этой точки в её движении вокруг полюса.
Уравнения, определяющие положение движущейся точки в зависимости от времени, называются уравнениями движения. Наиболее удобный способ задания движения точки — естественный способ. Сложное движение твёрдого тела. Сложение вращений тела вокруг пересекающихся осей. Кинематические уравнения Эйлера. Движение твёрдого тела называют сложным, если тело одновременно участвует как минимум в двух движениях. Относительным движением твёрдого тела называют его движение относительно подвижной системы координат. Переносным движением твёрдого тела называют его движение вместе с подвижной системой координат относительно неподвижной. При сложении вращений вокруг пересекающихся осей получаем вращательное движение, происходящее вокруг мгновенной оси вращения, с абсолютной угловой скоростью, равной геометрической сумме угловых скоростей составляющих вращение. Сложение вращений тела вокруг параллельных осей. Пара мгновенных вращений. Сложение вращений тела вокруг параллельных осей: · Вращения имеют одинаковые направления. Сложение двух одинаково направленных вращений вокруг параллельных осей приводит к одному вращению вокруг параллельной мгновенной оси вращения с угловой скоростью, равной сумме угловых скоростей составляющих вращений. · Вращения имеют противоположные направления с неравными угловыми скоростями. Сложение двух противоположно направленных вращений с неравными угловыми скоростями приводит к одному вращению вокруг параллельной мгновенной оси вращения с угловой скоростью, равной разности угловых скоростей составляющих вращений.
Пара вращений. Парой вращений называют совокупность двух вращений твёрдого тела вокруг параллельных осей с равными и противоположно направленными угловыми скоростями. Метод Виллиса. Метод Виллиса применяют для определения угловых скоростей зубчатых механизмов, в которых имеются зубчатые колёса, вращающиеся относительно подвижных осей. Метод Виллиса основан на теории сложения вращений вокруг параллельных осей. Зубчатые колёса учасвуют в двух движениях: 1) В относительном вращении зубчатых колёс по отношению к водилу. 2) В переносном вращении вместе с водилом вокруг его оси. При расчёте определяют зависимость между относительными угловыми скоростями, которые равны разности абсолютных и переносных угловых скоростей. В этом случае отношение между относительными угловыми скоростями обратно пропорциональны радиусам колём или числу зубьев, взятые со знаком минус, если зацепление внешнее, и со знаком плюс, если зацепление внутреннее.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 1442; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.177.116 (0.007 с.) |

 — угол собственного вращения;
— угол собственного вращения; — угол прецессии;
— угол прецессии; — угол нутации.
— угол нутации.



 -вектор угловой скорости,
-вектор угловой скорости,  -радиус-вектор данной точки относительно неподвижной оси.
-радиус-вектор данной точки относительно неподвижной оси. , h- кратчайшее расстояние точки до мгновенной оси вращения.
, h- кратчайшее расстояние точки до мгновенной оси вращения.



 - скорость точки
- скорость точки - скорость полюса
- скорость полюса - скорость точки во вращательном движении вокруг полюса
- скорость точки во вращательном движении вокруг полюса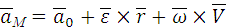
 - ускорение точки
- ускорение точки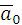 -ускорение начала подвижной системы координат
-ускорение начала подвижной системы координат -скорость точки
-скорость точки - угловое ускорение тела в подвижной системе координат
- угловое ускорение тела в подвижной системе координат



