
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Движение точки можно изучать используя любую систему координат. Рассмотрим случай декартовой прямоугольной системы координат.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
КИНЕМАТИКА 1)Предмет Механики….
ТМ изучает простейшую форму движения материи – мех-ое движ. Мех-ое движ – изменение с течение времени положения материальных тел или частиц одного и того же тела друг относительно друга. ТМ состоит из 3 разделов: статика – изучает усл-ия равновесия мат-ых тел; кинематика – изучает движение мат-ых тел без учёта действующих тел;; динамика – изучает движение мат-ых тел с учётом действующих тел. Кинематика и ее осн. задачи Кинематикой называется раздел теоретической механики, в котором механическое движение изучается только с его геометрической стороны, без учета взаимодействий, определяющих это движение. Механическое движение – это изменение положения тела в пространстве в функции времени. Положение тела обычно определяется по отношению к некоторой системе отсчета, неизменно связанной с др. телом, например, землей. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. В кинематике рассматриваются две основные задачи:
установление математических способов задания движения точки (тела) относительно выбранной системы отсчета, или установление закона движения точки (или тела);
определение по заданному закону движения тела всех кинематических характеристик этого движения (траекторий, скорости и ускорения точки или линейных скоростей и ускорений точек тела, угловых скоростей и угловых ускорений тела).
Время, как и пространство, существует объективно, независимо от нашего сознания. Время непрерывно и бесконечно; в классической механике оно принимается универсальным, т.е. одинаковым для всех систем отсчета.
Отсчет времени ведется от некоторого начального момента (t0 = 0), о выборе которого в каждом случае уславливаются. Всякий данный момент времени выражает собой число секунд, прошедших от начального момента времени до данного. Число секунд между двумя последовательными моментами времени называется промежутками времени
Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково. Кинематика делится на две части: кинематика точки и кинематика твердого тела. 3.Вект. способ задан. Движ точки….. Векторный способ. Будем рассматривать случай декартовой прямоугольной системы координат. Движение точки относительно рассматриваемой системы отсчета задано, если известен радиус-вектор
Векторный способ обычно применяется для теоретического изложения кинематики точки.
Траектория точки – непрерывная кривая, которую описывает точка при своем движении. Векторный сп. положение точки определяется ее радиус-вектором
Скорость точки при векторном способе задания движения
Средней скоростью
Рис. 1.4 Скорость точки равна первой производной по времени от ее радиус-вектора.
4. Координ. Способ задан. Движ точки…. Координатный способ. Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t). Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).
Пост. движ. Тверд тела. Существует пять видов движения твердого тела: 1. поступательное движение; 2. вращение вокруг неподвижной оси; 3. плоское движение; 4. вращение вокруг неподвижной точки; 5. свободное движение. Первые два называются простейшими движениями твердого тела: Вращ. движ тверд тела Равномерное вращение Вращение называется равномерным, если его угловая скорость постоянна, т.е. Так как
Равнопеременное вращение Вращение называется равноускоренным, если его угловое ускорение постоянно и больше нуля, т.е. Вращение называется равнозамедленным, если его угловое ускорение постоянно и меньше нуля, т.е. Так как
далее
или 11.Ск-ть и уск тверд тела… Сложное движение точки Основные понятия Во многих задачах движение точки приходится рассматривать относительно двух (и более) систем отсчета, движущихся друг относительно друга. В простейшем случае сложное движение точки состоит из относительного и переносного движений. Определим эти движения. Рассмотрим две системы отсчета движущиеся друг относительно друга. Одну систему отсчета O 1 x 1 y 1 z 1 примем за основную и неподвижную. Вторая система отсчета Oxyz будет двигаться относительно первой. Движение точки относительно подвижной системы отсчета Oxyz называется относительным. Характеристики этого движения, такие как, траектория, скорость и ускорение, называются относительными. Их обозначают индексом r. Движение точки относительно основной неподвижной системы отсчета O 1 x 1 y 1 z 1называется абсолютным (или сложным). Траектория, скорость и ускорение этого движения называются абсолютными. Их обозначают без индекса. Переносным движением точки называется движение, которое она совершает вместе с подвижной системой отсчета, как точка, жестко скрепленная с этой системой в рассматриваемый момент времени. Вследствие относительного движения движущаяся точка в различные моменты времени совпадает с различными точками тела S, с которым скреплена подвижная система отсчета. Переносной скоростью и переносным ускорением являются скорость и ускорение той точки тела S, с которой в данный момент совпадает движущаяся точка. Переносные скорость и ускорение обозначают индексом e. Если траектории всех точек тела S, скрепленного с подвижной системой отсчета, изобразить на рисунке, то получим семейство линий – семейство траекторий переносного движения точки М. Вследствие относительного движения точки М в каждый момент времени она находится на одной из траекторий переносного движения. Одно и то же абсолютное движение, выбирая различные подвижные системы отсчета, можно считать состоящим из разных переносных и соответственно относительных движений. Сложение скоростей Определим скорость абсолютного движения точки М, если известны скорости абсолютного и переносного движений этой точки.
Деля обе части равенства на
Формулы Пуассона Производные по времени от единичных векторов определим по формулам Пуассона Вектор
Ускорение Кориолиса
Ускорение Кориолиса Теорема (Правило Жуковского). Модуль ускорения Кориолиса равен удвоенному произведению угловой скорости переносного вращения на модуль проекции относительной скорости на плоскость, перпендикулярную оси переносного вращения; чтобы получить направление ускорения Кориолиса, необходимо вектор проекции относительной скорости повернуть на
17. Плоск движ тверд тела и движ плоск фигуры….. И вращательное движения.
Теорема. Любое движение твердого тела, в том числе и движение плоской фигуры в ее плоскости, бесчисленным множеством способов можно разложить на два движения, одно из которых переносное, а другое – относительное.
Для доказательства этого достаточно показать, что плоскую фигуру в ее плоскости из одного положения в любое другое можно перевести двумя перемещениями – поступательным перемещением в плоскости фигуры вместе с каким –либо полюсом и поворотом в той же плоскости вокруг этого полюса. Рис. 6-4 Рассмотрим два любых положения плоской фигуры 1 и 2. Выделим отрезок АB в рассматриваемой фигуре. Перевод фигуры из положения 1 в положение 2 можно рассматривать как суперпозицию двух движений: поступательного из 1 в 1' и вращательного из 1' в 2 вокруг точки A', называемой обычно полюсом (рис. 6-4а). Существенно, что в качестве полюса можно выбрать любую точку, принадлежащую фигуре или даже лежащую в плоскости вне фигуры. На рис. 6-4б, к примеру, в качестве полюса выбрана точка В. Обратите внимание: длина пути при поступательном перемещении изменилась (в данном случае увеличилась), но угол поворота остался прежним!
Метод Виллиса. Метод Виллиса применяют для определения угловых скоростей зубчатых механизмов, в которых имеются зубчатые колёса, вращающиеся относительно подвижных осей. Метод Виллиса основан на теории сложения вращений вокруг параллельных осей. Зубчатые колёса учасвуют в двух движениях: 1) В относительном вращении зубчатых колёс по отношению к водилу. 2) В переносном вращении вместе с водилом вокруг его оси. При расчёте определяют зависимость между относительными угловыми скоростями, которые равны разности абсолютных и переносных угловых скоростей. В этом случае отношение между относительными угловыми скоростями обратно пропорциональны радиусам колём или числу зубьев, взятые со знаком минус, если зацепление внешнее, и со знаком плюс, если зацепление внутреннее. КИНЕМАТИКА 1)Предмет Механики….
ТМ изучает простейшую форму движения материи – мех-ое движ. Мех-ое движ – изменение с течение времени положения материальных тел или частиц одного и того же тела друг относительно друга. ТМ состоит из 3 разделов: статика – изучает усл-ия равновесия мат-ых тел; кинематика – изучает движение мат-ых тел без учёта действующих тел;; динамика – изучает движение мат-ых тел с учётом действующих тел. Кинематика и ее осн. задачи Кинематикой называется раздел теоретической механики, в котором механическое движение изучается только с его геометрической стороны, без учета взаимодействий, определяющих это движение. Механическое движение – это изменение положения тела в пространстве в функции времени. Положение тела обычно определяется по отношению к некоторой системе отсчета, неизменно связанной с др. телом, например, землей. Движение материальных объектов всегда происходит в пространстве относительно определенной системы отсчета и во времени. Пространство считается трехмерным эвклидовым пространством, свойства которого не зависят от движущихся в нем материальных объектов. В кинематике рассматриваются две основные задачи:
установление математических способов задания движения точки (тела) относительно выбранной системы отсчета, или установление закона движения точки (или тела);
определение по заданному закону движения тела всех кинематических характеристик этого движения (траекторий, скорости и ускорения точки или линейных скоростей и ускорений точек тела, угловых скоростей и угловых ускорений тела).
Время, как и пространство, существует объективно, независимо от нашего сознания. Время непрерывно и бесконечно; в классической механике оно принимается универсальным, т.е. одинаковым для всех систем отсчета.
Отсчет времени ведется от некоторого начального момента (t0 = 0), о выборе которого в каждом случае уславливаются. Всякий данный момент времени выражает собой число секунд, прошедших от начального момента времени до данного. Число секунд между двумя последовательными моментами времени называется промежутками времени
Время в классической механике не связано с пространством и движением материальных объектов. Во всех системах отсчета движущихся друг относительно друга оно протекает одинаково. Кинематика делится на две части: кинематика точки и кинематика твердого тела. 3.Вект. способ задан. Движ точки….. Векторный способ. Будем рассматривать случай декартовой прямоугольной системы координат. Движение точки относительно рассматриваемой системы отсчета задано, если известен радиус-вектор
Векторный способ обычно применяется для теоретического изложения кинематики точки.
Траектория точки – непрерывная кривая, которую описывает точка при своем движении. Векторный сп. положение точки определяется ее радиус-вектором
Скорость точки при векторном способе задания движения
Средней скоростью
Рис. 1.4 Скорость точки равна первой производной по времени от ее радиус-вектора.
4. Координ. Способ задан. Движ точки…. Координатный способ. Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t). Если движение в плоскости, то два уравнения движения. Уравнения движения описывают уравнение траектории в параметрической форме. Исключив из уравнений параметр t, получаем уравнение траектории в обычном виде: f(x,y)=0 (для плоск-ти).
Движение точки можно изучать используя любую систему координат. Рассмотрим случай декартовой прямоугольной системы координат.
|
||||
|
Последнее изменение этой страницы: 2016-08-10; просмотров: 752; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |



 этой точки как функция времени, т.е.
этой точки как функция времени, т.е. (1-1)
(1-1) , проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.
, проведенным из какого-либо центра. Кривая, которая вычерчивается концом какого-либо вектора, назыв. годографом этого вектора. Т.е. траектория – годограф радиус-вектора.
 Положение движущейся точки М относительно системы отсчета в момент времени
Положение движущейся точки М относительно системы отсчета в момент времени 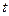 определяется радиус-вектором
определяется радиус-вектором  . В другой момент времени
. В другой момент времени 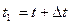 точка займет положение М 1 с радиус-вектором
точка займет положение М 1 с радиус-вектором  . За время
. За время  радиус-вектор движущейся точки изменится на
радиус-вектор движущейся точки изменится на  .
. называется отношение изменения радиус-вектора
называется отношение изменения радиус-вектора  к изменению времени
к изменению времени  (1-4)
(1-4) (1-5)
(1-5) .
.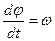 , то
, то  . Начальные условия:
. Начальные условия: 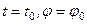 , то после интегрирования получим
, то после интегрирования получим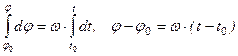 или
или 

 .
. .
. , то
, то  . Начальные условия:
. Начальные условия:  , то после интегрирования получим
, то после интегрирования получим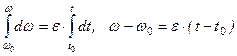 или
или 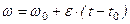

 и после интегрирования,
и после интегрирования,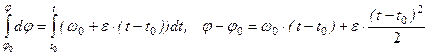


 вдоль траектории
вдоль траектории  точка М совершит относительное перемещение, определяемое вектором
точка М совершит относительное перемещение, определяемое вектором  . Сама кривая
. Сама кривая  Одновременно та точка
Одновременно та точка  кривой
кривой  . В результате точка
. В результате точка  совершит перемещение
совершит перемещение  .
.

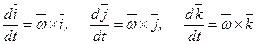
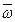 - это угловая скорость вращательной части движения вокруг точки О подвижной системы отсчета относительно неподвижной.
- это угловая скорость вращательной части движения вокруг точки О подвижной системы отсчета относительно неподвижной.
 – ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: ас= 2×|we×vr|×sin(we^vr), направление вектора
– ускорение Кориолиса (кориолисово ускорение) – в случае непоступательного переносного движения абсолютное ускорение = геометрической сумме переносного, относительного и кориолисова ускорений. Кориолисово ускорение характеризует: 1) изменение модуля и направления переносной скорости точки из-за ее относительного движения; 2) изменение направления относительной скорости точки из-за вращательного переносного движения. Модуль ускорения Кориолиса: ас= 2×|we×vr|×sin(we^vr), направление вектора  определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90о в направлении вращения.
определяется по правилу векторного произведения, или по правилу Жуковского: проекцию относительной скорости на плоскость, перпендикулярную переносной угловой скорости, надо повернуть на 90о в направлении вращения. Кориолисово уск. = 0 в трех случаях: 1) we=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(we^vr)=0, т.е. Ð(we^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором we = 90о, sin90o=1, ас=2×we×vr.
Кориолисово уск. = 0 в трех случаях: 1) we=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(we^vr)=0, т.е. Ð(we^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором we = 90о, sin90o=1, ас=2×we×vr. вокруг оси, параллельной оси переносного вращения в направлении этого вращения.
вокруг оси, параллельной оси переносного вращения в направлении этого вращения. В частности, движение плоской фигуры в ее плоскости относительно системы
В частности, движение плоской фигуры в ее плоскости относительно системы  , расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат
, расположенной в той же плоскости, можно разложить на переносное и относительное движения следующим образом. Примем за переносное движение фигуры ее движение вместе с поступательно движущейся системой координат  , начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат
, начало которой скреплено с точкой О фигуры, принятой за полюс. Тогда относительное движение фигуры будет по отношению к подвижной системе координат 


